Svar på opgave 1: Rejsen til New York

1. De sparer: (20.861 - 17.935) kr. = 2.926 kr.
2. De sparer: (12 timer + 55 min.) - (8 timer + 25 min.) =
   (12 - 8) timer + (55 - 25) min. =
   4 timer og 30 min.
3. Gennemsnitsfarten er distance/tid. Med enheden km/t får man:
   (6.206 km)/(8 timer 25 min.) =
   (6.206 km)/(8 + 25/60 timer)) =
   6.206/8,417 km/t =
   737 km/t
4. Charlottes familie bruger 17.935 kr. på rejsen, der koster 4.484 kr/person. Antallet af personer i familien er derfor: 17.935 kr./(4.484 kr./person) = 4 personer
5. Deres udgifyer til mad er: 4·7·40 USD = 1120 USD = 11,2·(100 USD) = 11,2·(563,52 DKK) = 6.311 kr.

Svar på opgave 2: Fra fahrenheit til celsius

1. 102 °F svarer til: (102 - 32)·5/9 °C = 38,9 °C
2. Nedenunder er sammenhængen mellem celcius-temperaturen og fahrenheit-temperaturen tegnet i Geogebra.
   
3. Punktet hvor grafen skærer x-aksen (32,0) viser, at temperaturen er 32 °F ved 0 °C.
4. Fahrenheit-temperaturen kaldes x. Man skal løse følgende ulighed med hensyn til x:
   38 < (x - 32)·(5/9) ⇔
   38 < x·(5/9) - 32·(5/9) ⇔
   38 + 32·(5/9) < x·5/9 ⇔
   55,778 < x·5/9 ⇔
   x > 100,4
   Det vil sige, at når celcius-temperaturen er over 38 °C, så er fahrenheit-temperaturen over 100,4 °F
5. y = (5/9)·x - 32·5/9 ⇒ y = 0,556·x - 17,8

Svar på opgave 3: Højde og vægt

1. Idealvægten for en mand på 180 cm er 71 kg. Dette aflæses på grafen som vist nedenfor:
   
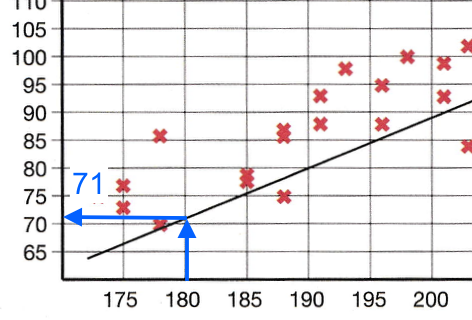
2. Spillernes højde aflæses til 198 cm henholdsvis 206 cm som vist nedenfor:
   
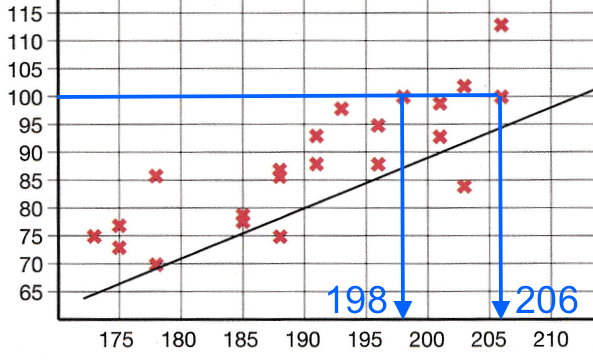
   Forskellen på spillernes højde er 206 cm - 198 cm = 8 cm
3. Spilleren med en højde på 213 cm har en idealvægt på 102 kg., mens han vejer 132 kg. For at være inde for normalvægten for hans højde, skal han veje mellem 102 ± 102·10% = 102 ± 10,2. Det vil sige, at hans normalvægt er mellem 91,8 kg. og 112,2 kg.
   
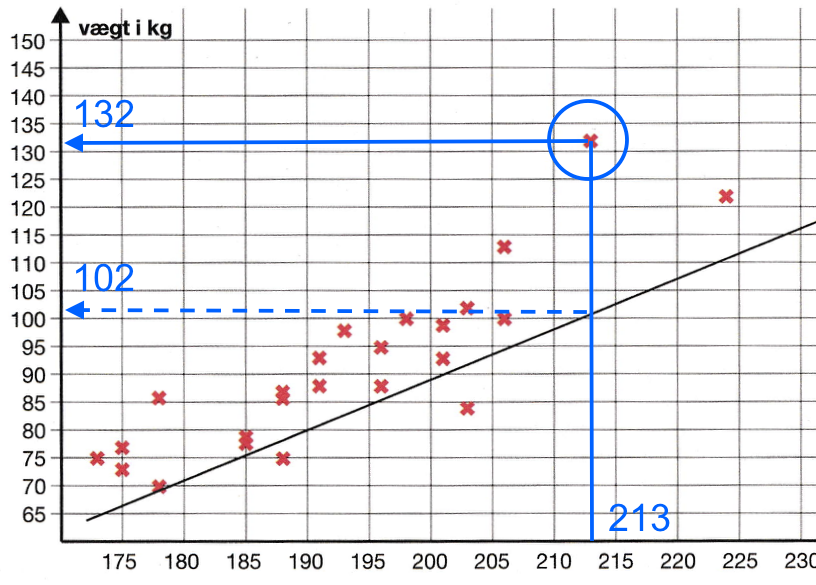
   Det vil sige, at spilleren med en højde på 213 cm har ikke normalvægt
4. Arket er udfyldt nedenunder.
   
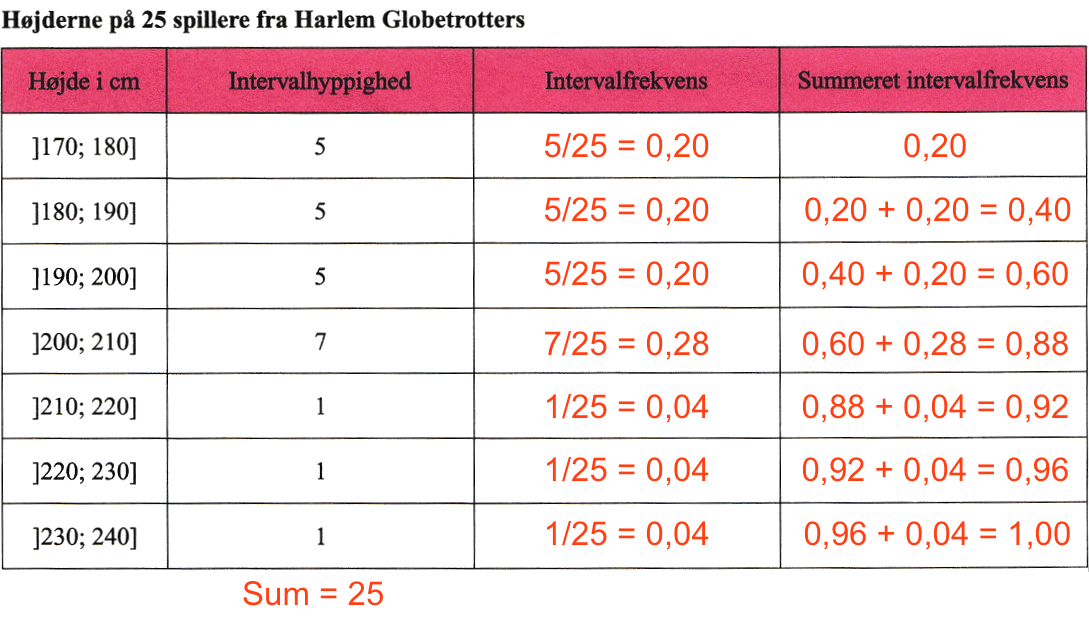
5. De danske mænds gennemsnitshøjde findes ved at tage midtpunktet for hvert interval til venstre og gange med frekvensen i tredje kolonne. Disse produkter summeres: (150 cm)·0,004 + (165 cm)·0,038 + (175 cm)·0,332 + (185 cm)·0,491 + (195 cm)·0,129 + (205 cm)·0,006 = 182,19 cm.
   For Harlem Globetrotters får man tilsvarende: (175 cm)·0,20 + (185 cm)·0,20 + (195 cm)·0,20 + (205 cm)·0,28 + (215 cm)·0,04 + (225 cm)·0,04 + (235 cm)·0,04 = 195,40 cm. Forskellen på gennemsnitshøjden af Harlem Globetrotters og danske mænd er 195,40 cm - 182,19 cm = 13,2 cm
6. Nedenfor er vist de to boksplot for højdefordelingen af danske mænd og spillerne i Harlem Globetrotters.
   
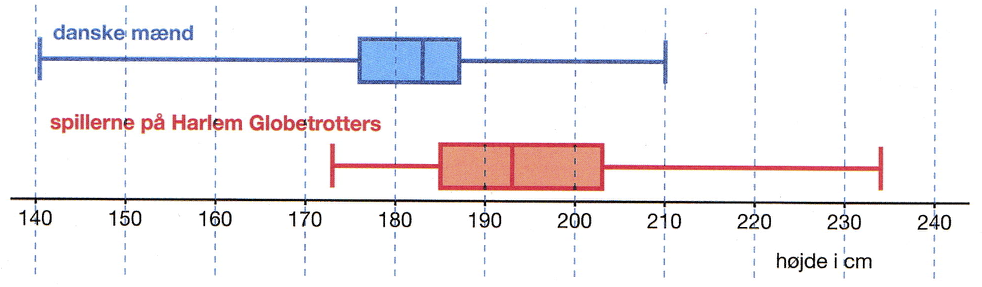
   Variationsbredden for danske mænd er 210 - 140 cm = 70 cm. For spillerne i Harlem GLobetrotters er den 234 cm - 173 cm = 61 cm. Det vil sige, at variationsbredden for højden for danske mænd er større end den for spillerne i Harlem Globetrotters.
   Medianen (den midterste linje i de to firkanter) er 183 cm for danske mænd, mens den er 193 cm for spillerne i Harlem Globetrotters.

Svar på opgave 4: Sukkerroer

1. Rumfang af prisme = længde gange areal af grundflade. Grundfladen er en trekant, der har arealet 0,5 gange højde gange grundlinje.
   Dette giver rumfanget: (35 m)·[0,5·(3 m)·(8 m)] = 420 m³
2. Man skal regne ud hvad 33 tons roer fylder. Hvis det er mere end 48 m³ roer, skal man laste 48 m³ ad gangen, ellers skal man laste 33 tons roer pr. lastbil.
   Man får, at 33 tons fylder: 33 tons/(0,70 tons/m³) = 47,14 m³. Da dette er mindre end 48 m³ skal hver lastbil lastes med 33 tons (eller 47,14 m³).
   Man regner ud, hvor mange lastbiler med 47,14 m³ i hver der skal til for at flytte 420 m³:
   420 m³/(47,14 m³) = 8,9 gange. Det vil sige, at lastbilen skal køre 9 gange for at flytte roerne.
3. Sukkerindholdet er (33 tons)·(90 %)·(17 %) = 5,05 tons sukker
4. Sukkeret udgør en andel på: (87 %)·(18 %) = 0,157 = 15,7 %

Svar på opgave 5: Afstand til en båd

1. Vinklen ved båden findes ved hjælp af reglen om, at summen af vinklerne i en treklant er 180°. Man får, at vinklen = 180° - (90° + 79°) = 11°
2. Bådens placering kaldes E. Afstanden mellem båden og B er lig med |DE|. Da trekant ABE er retvinklet gælder, at tangens til en af dens spidse vinkler er lig med længde af vinklens modstående side divideret med vinklens hosliggende side. Disse sider er vist med rødt på nedenstående tegning lavet i Geogebra:
   
   Det vil sige, at tan(11°) = (12 m)/|BE| ⇒ |BE| = (12 m)/tan(11°) = 61,7 m
3. Man skal finde |DE|. Trekant CDE og trekant ABE er retvinklede og ensvinklede. Dette kan i første omgang bruges til at finde |CD|:
   |CD|/|AB| = |CE|/|BE| ⇒
   |CD|/12 = 71,7/61,7 ⇒
   |CD|= 12·71,7/61,7 = 13,94
   Man kan nu finde |DE| ved hjælp af Pythagoras læresætning:
   |DE|² = |CD|² + |CE|² ⇒
   |DE|² = 13,94² + 71,7² ⇒
   |DE|² = 5335,21 ⇒
   |DE| = √5335,21 ⇔
   |DE| = 73,04
   Det vil sige, at afstanden fra punkt D til båden er 73 m

Svar på opgave 6: Regulær ottekant

1. Summen af vinklerne i ottekanten er summen af vinklerne i de tre firkanter, som den er inddelt i. De tre firkanter har hver vinkelsummen 360°, og tilsammen giver det 3·360° = 1080°
2. Nedenunder er midtnormalerne til AB og BC tegnet i Geogebra:
   
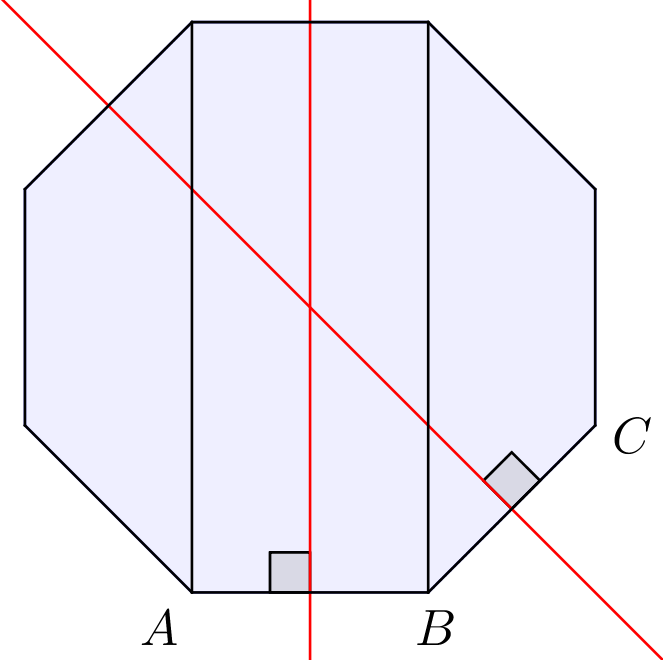
3. På nedenstående tegning lavet i Geogebra er fire trekanter: ΔAIO, ΔBIO, ΔBJO og ΔCJO:
   
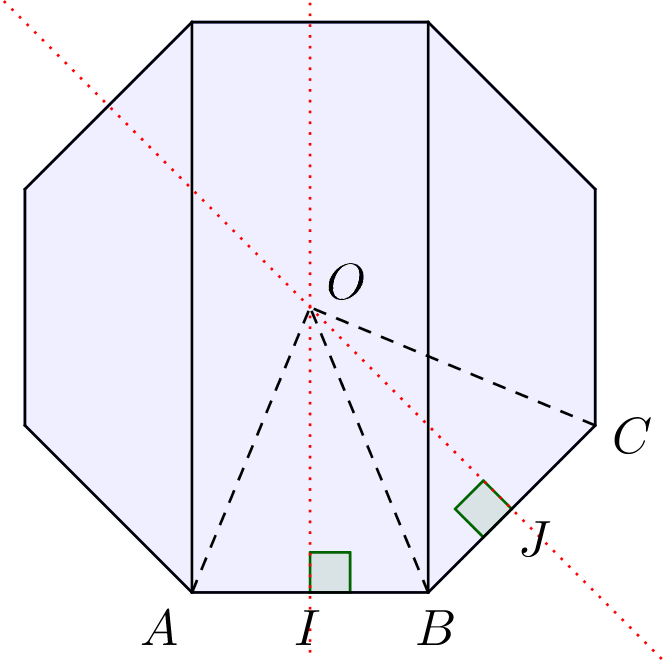
   Man skal vise, at disse trekanter er ens og dermed at: |AO| = |CO|. Man starter med at vise, at ΔBIO, ΔBJO:
   I er midpunktet af AB og J er midpunktet af BC.
   De to trekanter deler siden BO, det vil sige, at denne side er ens for begge. De er begge retvinlede, da de indeholder hver sin midtnormal. Det vil sige, at de to trelanter har en vinkel til fælles. Siderne BI og CJ er ens, da de er det halve af siden i en regulær polygon, der har lutter ens sider.
   Da ΔBIO og ΔBJO har en vinkel og to sider til fælles er de ens (kongruente).
   ΔAIO er lig med ΔBIO. Det følger af, at de begge er retvinklede, at de har siden IO til fælles, og at |AI| = |BI|.
   Tilsvarende gælder, at ΔBJO = ΔCJO. Da ΔAIO = ΔBIO = ΔBJO = ΔCJO gælder, at |AO| = |CO|.
4. Nedenunder er den omskrevne cirkel til den regulære ottekant tegnet i Geogebra. Dens centrum er O, de to midtnormalers skæringspunkt.
   
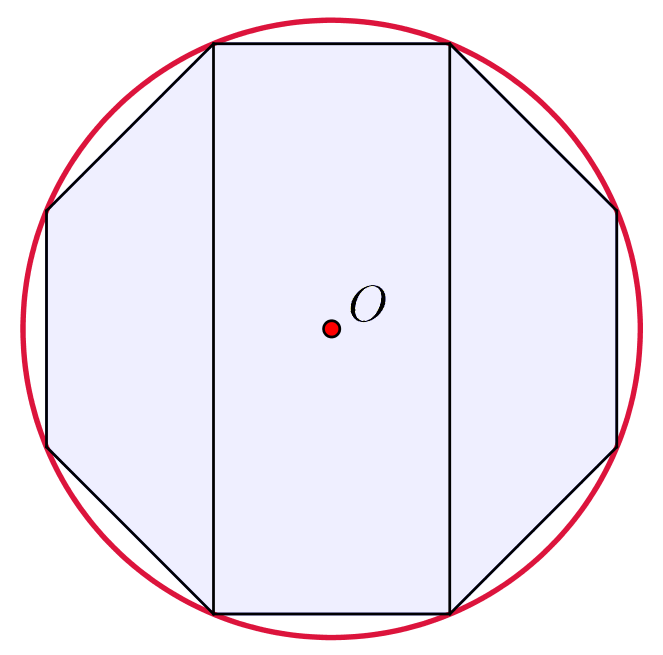
5. Man får d = (4 cm)/sin(22,5°) = (4 cm)/0,3827 = 10,5 cm