Svar på opgave 1: Skibsfart i Danmark

1. Nedgangen i indtjening fra 2008 til 2009 var 190 mia. kr. - 140 mia. kr. = 50 mia. kr.
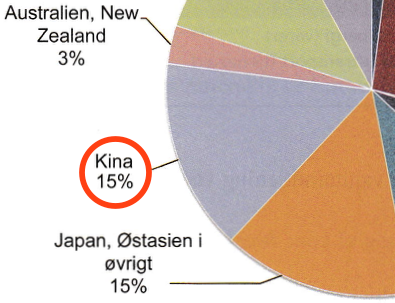
2. Valutaindtjeningen på skibsfart til og fra Kina var i 2010: (15 %)·(175 mia. kr.) = 26,25 mia. kr.
   De 15 % er aflæst af diagrammet som vist:
   
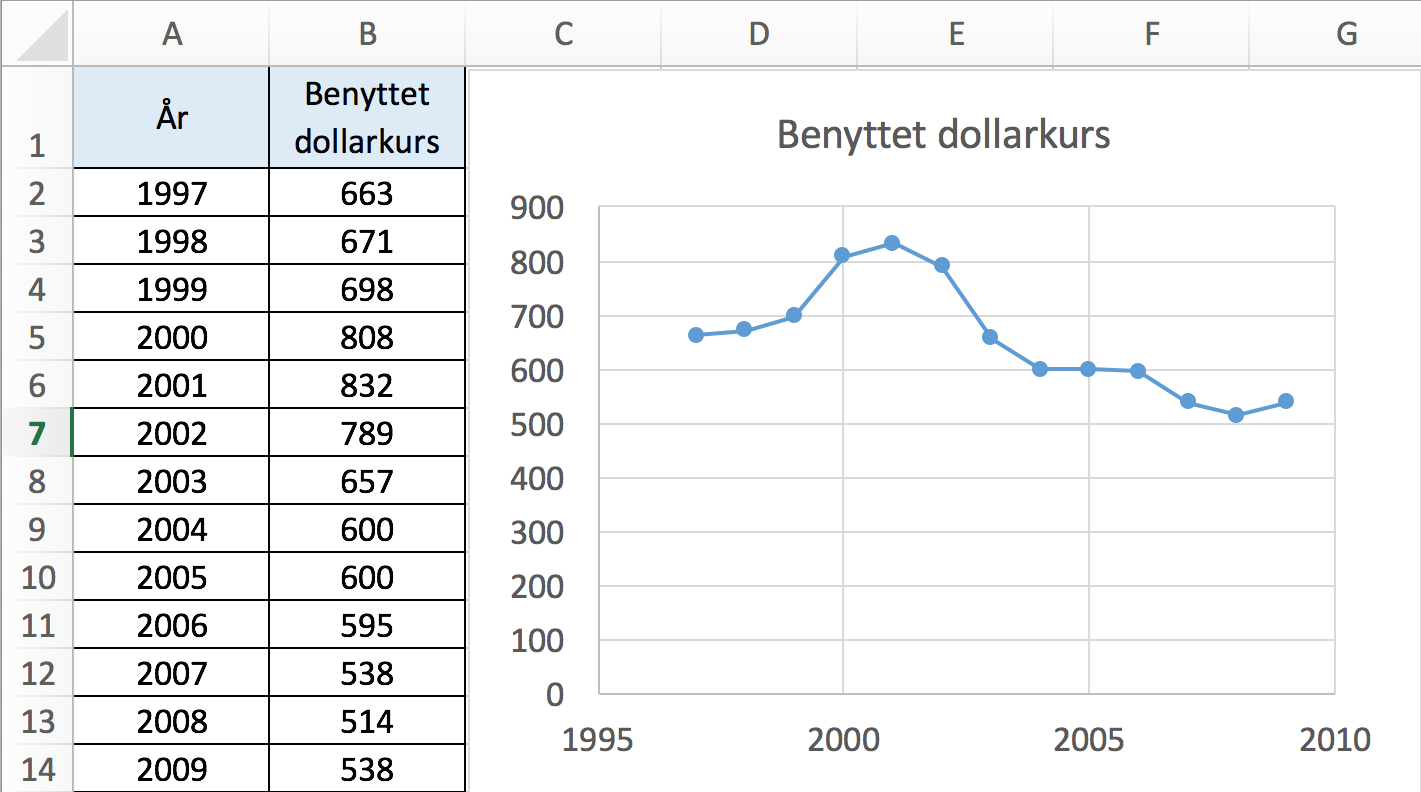
3. Nedenfor er vist udviklingen i dollarkursen lavet i Excel.
   
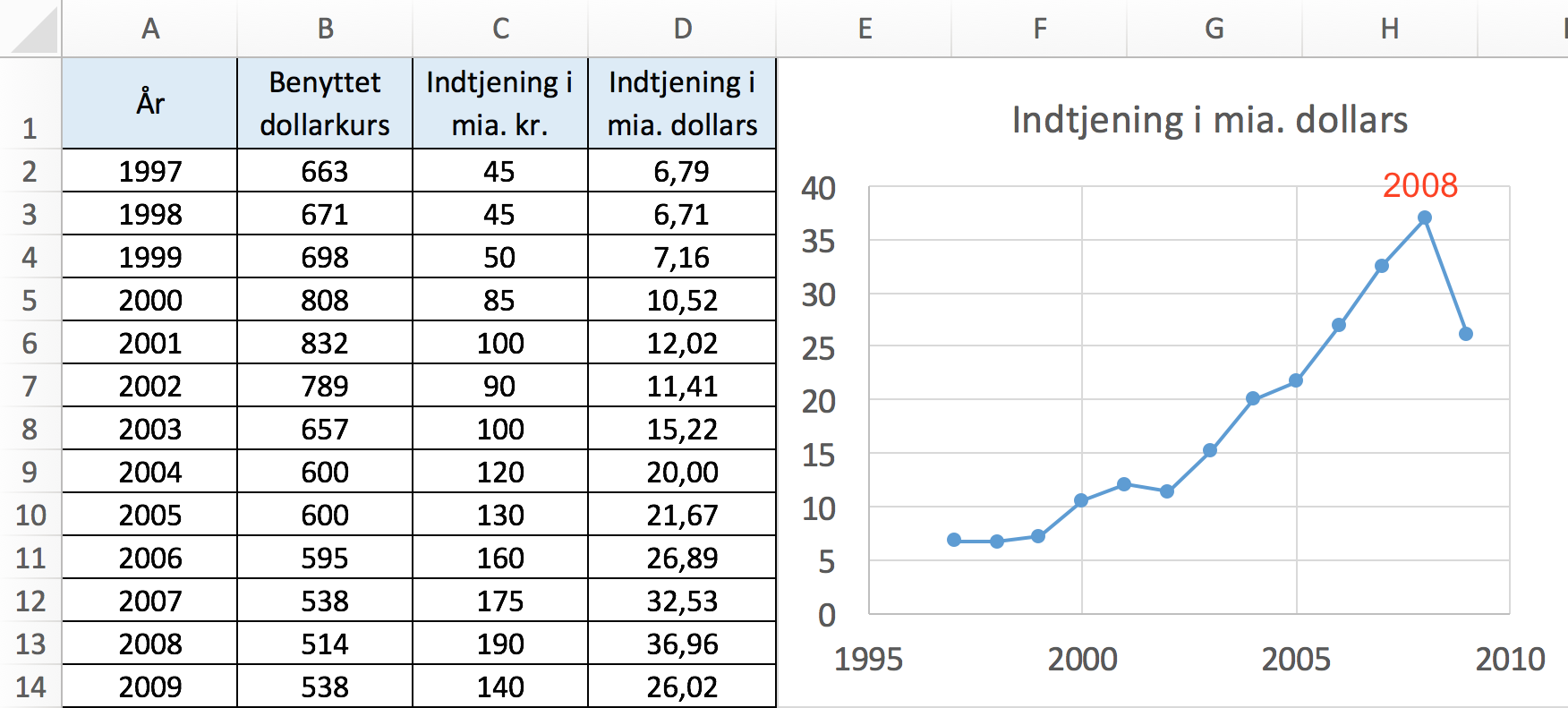
4. Det år, hvor indtjeningen målt i dollars var størst, var 2008 som vist nedenunder i Excel-diagrammet.
   I kolonnen med indtjening i dollars er brugt formlen =C2/B2*100. Dette er så gentaget nedefter fra celle D3 til celle D14.
   
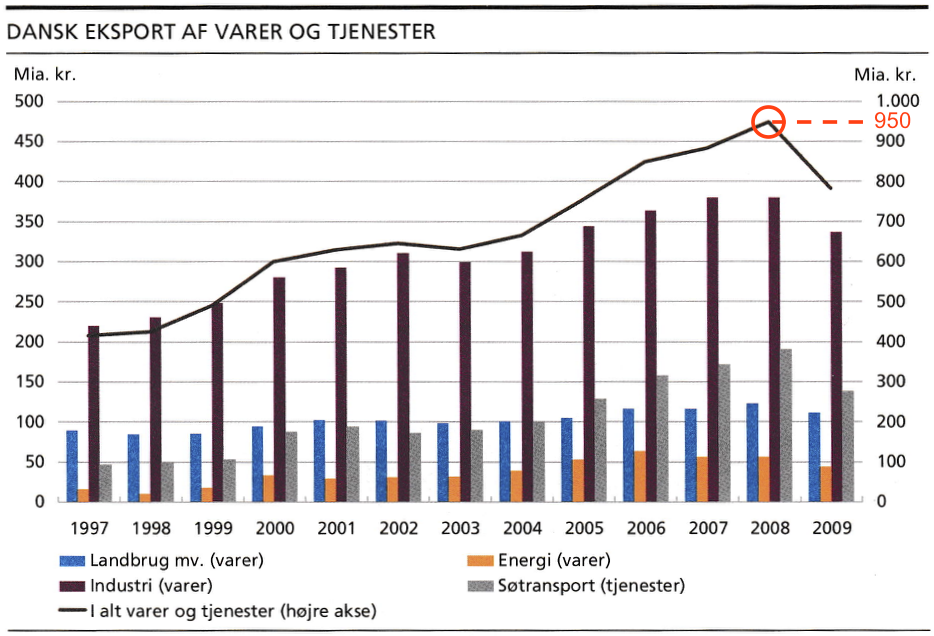
5. Den samlede valutaindtjening i 2008 var 950 mia. kr. som vist på diagrammet nedenunder.
   
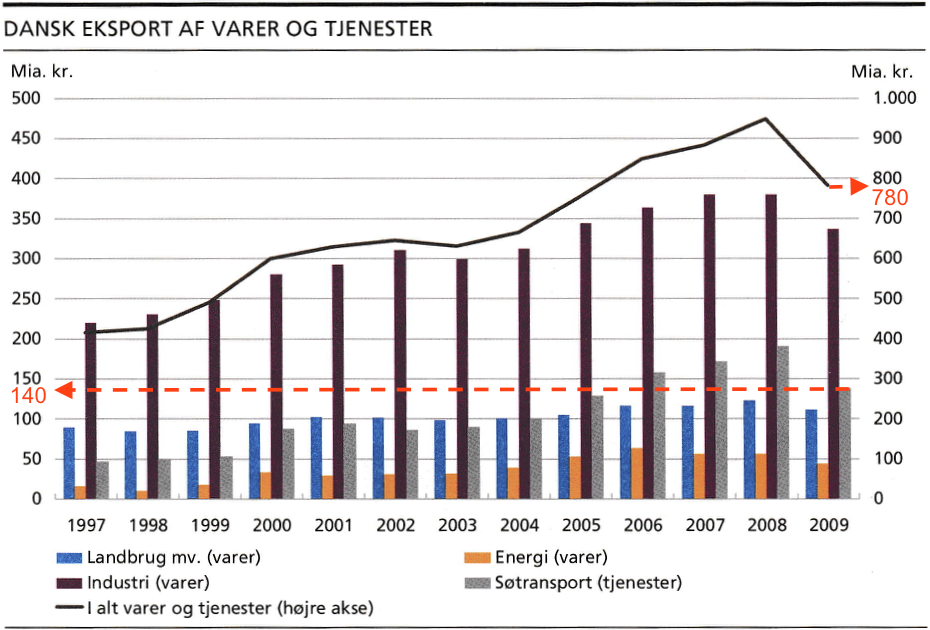
6. I 2009 var den samlede indtjening 780 mia. kr. og indtjeningen fra søfart var 140 mia. kr. Dette er vist på diagrammet nedenunder.
   Forholdet er (140/780)·100 % = 17,9487 % = 18 %
   

Svar på opgave 2: Containerskib

1. Længden af en container målt i cm er antal fod gange antal cm pr. fod =
   (20 fod)·(30,48 cm/fod) = (20·30,48) fod·cm/fod = 609,60 cm ≈ 610 cm
2. Rumfanget af en 20 fods container er dens længde gange dens bredde gange dens højde. Dette giver rumfanget:
   (610 cm)·(244 cm)·(274 cm) = (610·244·274) cm³ = 40.782.160 cm³ = 40.782.160 (0,01 m)³ =
   40.782.160·(0,01)³ m³ = 40.782.160·0,000001 m³ = 40,8 m³ ≈ 40 m³
3. TEU står for Twenty-foot Equivalent Units dvs. "hvad der svarer til en 20 fods container".
   20 fods containerne udgør tilsammen 3417 TEU.
   En 40 fods container svarer til 2 TEU. Tilsammen svarer 40 fods containerne til 3512·2 TEU = 7024 TEU.
   Antallet af TEU er dermed 3417 TEU + 7024 TEU = 10.441 TEU
4. Antallet af 20 fods containere kaldes x og antallet af 40 fods containere kaldes y. Dette giver følgende to ligninger med hensyn til x og y:
   Antallet af 20 fods contaonere og 40 fods containere skal være 10.000 tilsammen: x + y = 10.000
   ANtallet af TEU skal være 12500 TEU: x + 2·y = 12.500. Disse ligninger løses:
   x + y = 10.000 og x + 2·y = 12.500 ⇔
   x = 10.000 - y og (10000 - y) + 2·y = 12.500 ⇔
   x = 10.000 - y og y = 12.500 - 10.000 ⇔
   x = 10.000 - 2.500 og y = 2.500 ⇔
   x = 7.500 og y = 2.500
   Dvs. der er 7.500 20 fods containere og 2.500 40 fods containere.
5. Skibstransporten er 134.000.000 TEU i 2009. Der er 11 år fra 2009 til 2020. Transportmængden stiger med 3,5 % hvert år. Dvs. i 2020 vil transporten være:
   (134.000.000 TEU)·(1 + 3,5 %)¹¹ =
   (134.000.000 TEU)·1,035¹¹ =
   (134.000.000 TEU)·1,45997 =
   195.636.000 TEU = 196 mio. TEU
6. Den samlede transport af bulkvarer gange 85 % er lig med søtransportens andel af bulkvarer. Det vil sige, at 15 % af den samlede transport foregik på andre måder end skibstransport.
   Man kalder den samlede transport for x. Man skal finde (15 %)·x. Man ved, at (85 %)·x = 4.612.000.000.
   Det giver, at x = 4.612.000.000/(85 %) og dermed er x·(15 %) =
   [4.612.000.000/(85 %)]·(15 %) =
   4.612.000.000·(15/85) =
   813.882.000
   Dvs. transporten af bulkvarer i 2009 på andet end søtransport var 814 mio. tons i 2009.
7. Den gennemsnitlige transport pr. person var vægt af transporterede varer divideret med antal personer i verden. Dette giver:
   (7849 mio. tons)/(6,8 mia.) =
   (7849 mio. tons)/(6800 mio.) =
   (7849 tons)/6800 =
   (7849/6800)·1000 kg = 1154,26 kg
   Dvs. der blev transporteret 1154 kg pr. person i verden ved søtransport i 2009.

Svar på opgave 3: Containerkode

1. Ejerkoden består af tre bogstaver, der kan vælges frit mellem 26 bogstaver.
   Dvs. at der er 26·26·26 = 17.576 kombinationer for ejerkoden.
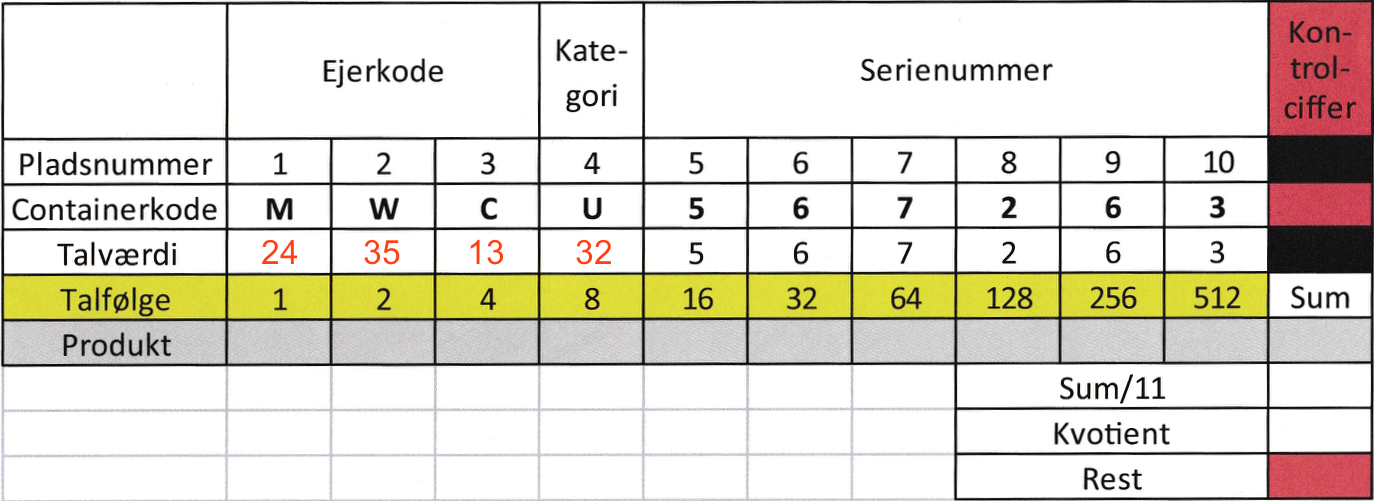
2. Tallene, der svarer til bogstaverne, er vist med røde tal i skemaet nedenunder.
   
3. Talfølgen er vist nedenunder.
   
   Systemet består i at det næste tal hele tiden er det dobbelte af det foregående. Det kan også beskrives som talfølgen 2ⁿ (2 i n'te) hvor n er pladsen i talfølgen. Talfølgen med n er vist nendenunder.
   
4. 4000 = 363·11 + 7.
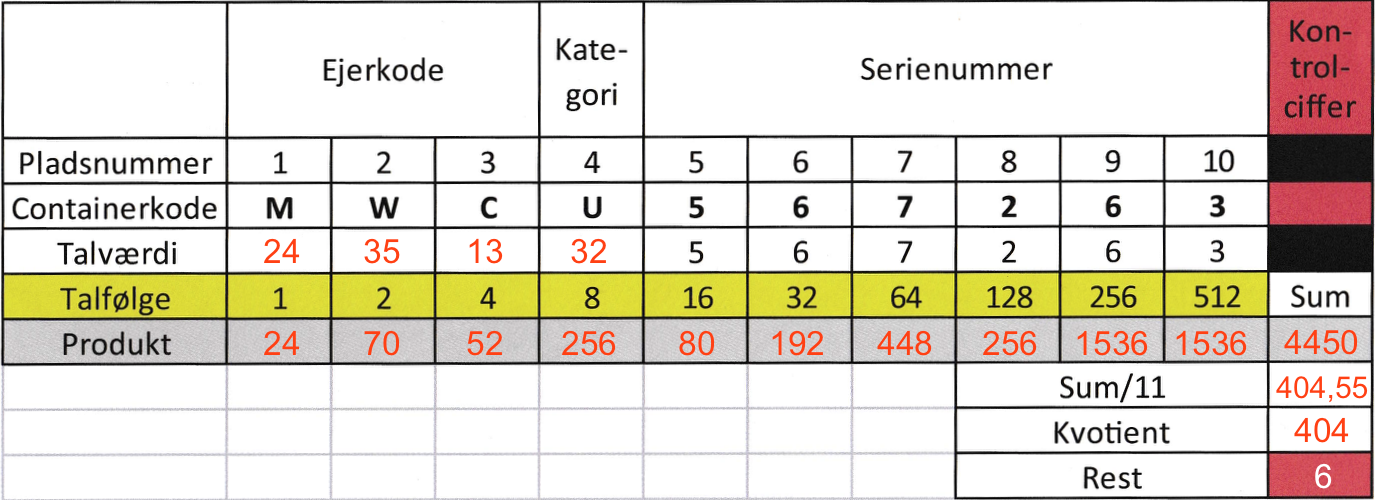
5. Skemaet er udfyldt nedenunder. Man får kontrolciffret 6, idet 4450 - 11·404 = 6.
   

Svar på opgave 4: Aarhus havn

1. Nedenfor er en beskåret udgave af kortet over havnen tegnet ind i Geogebra. Billedet er tilpasset i størrelsen, så afstanden fra 0 til 500 på x-aksen i koordinatsystemet svarer til målestokkens længde.
   Ved hjælp af linjestykke-værktøjet måles kajens længde til 1290 m
   
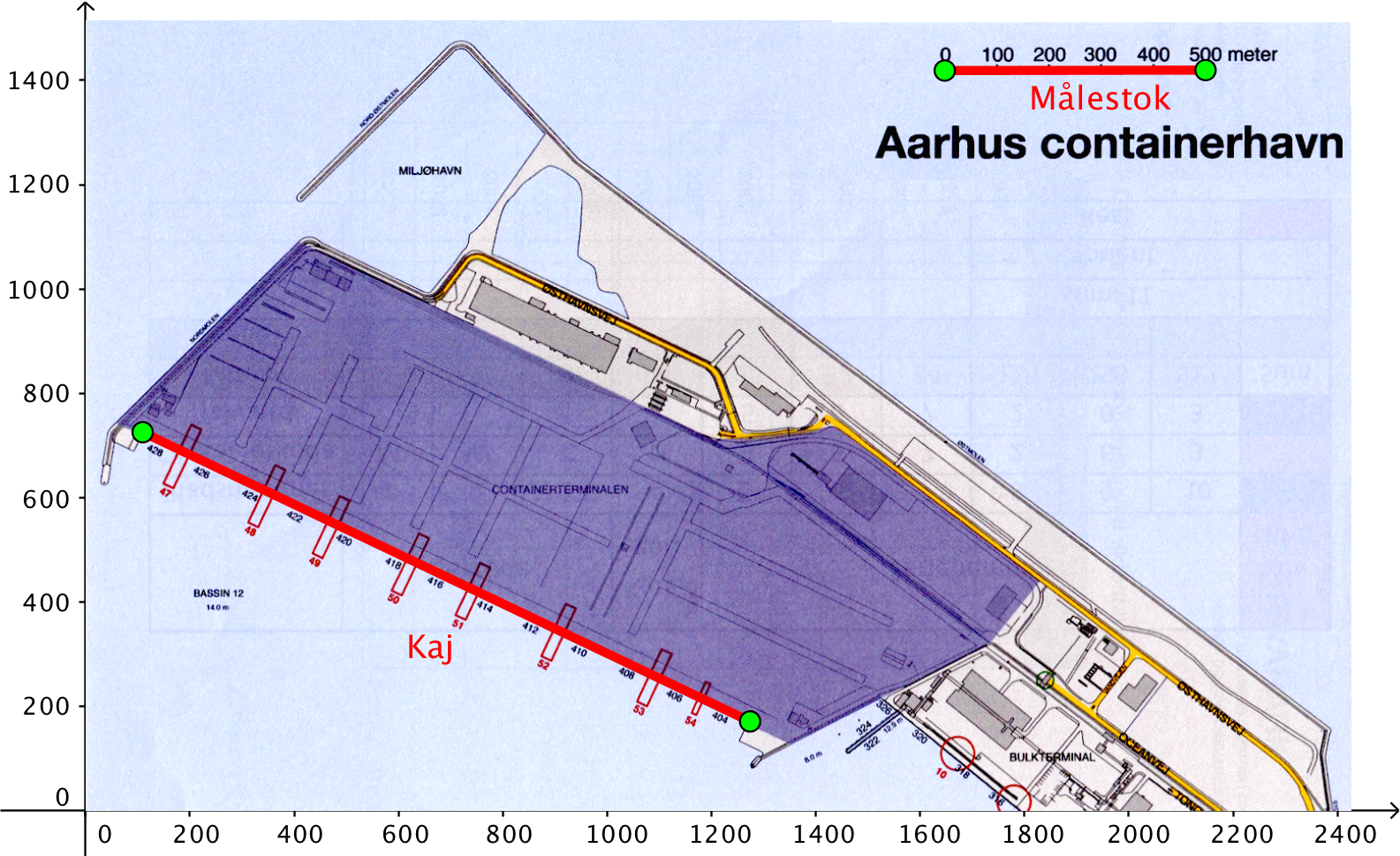
2. På billedet nedenunder er terminalområdets areal målt til 744657,66 m² ≈ 745.000 m² med Geogebras polygon-værktøj. Dvs. oplysningen passer
   
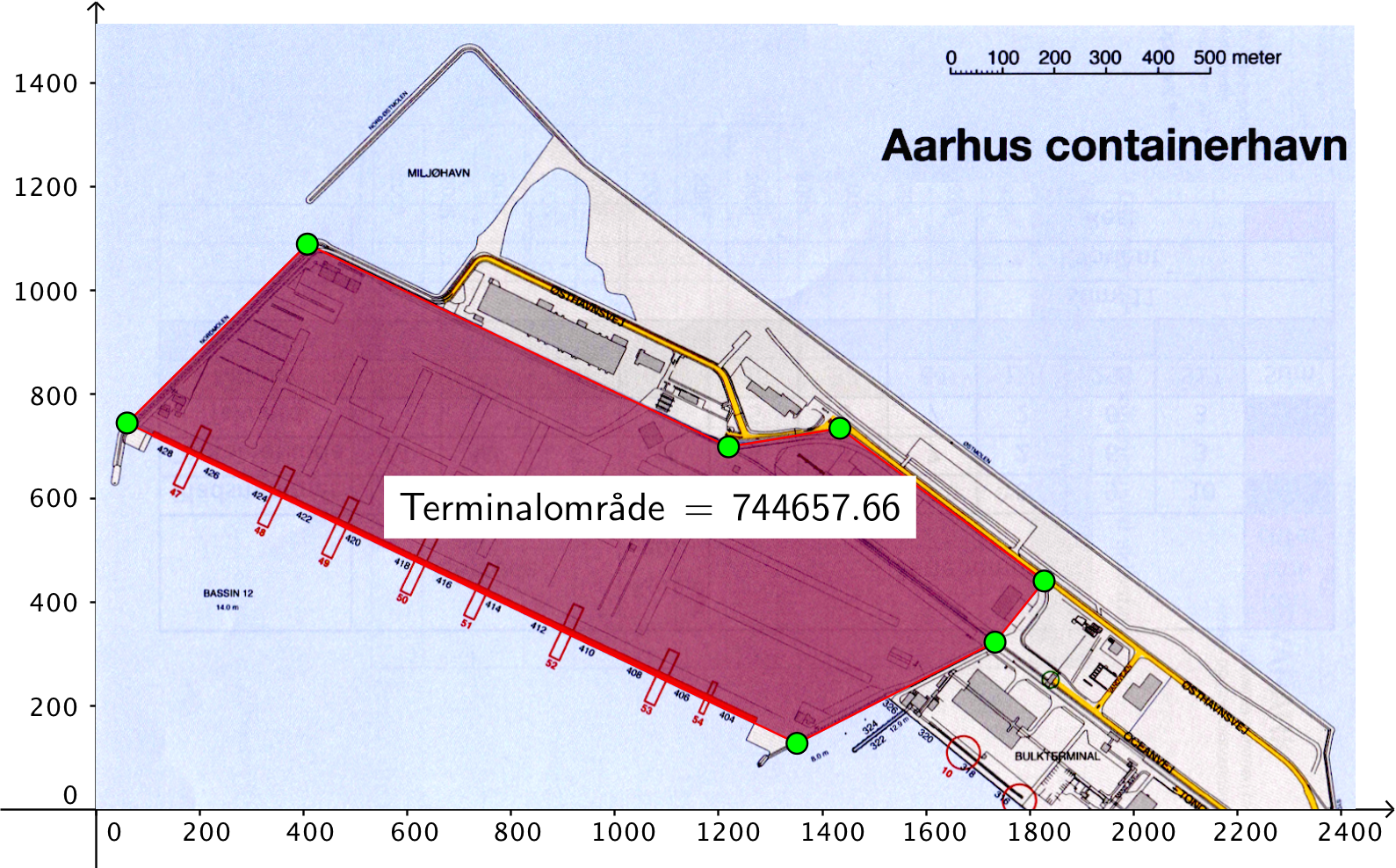
3. Det ses af skemaet at Slipner ankommer den 4/3 kl. 18:00 og afgår den 5/3 00:30.
   Der er 6 timer fra kl. 18 til midnat. Dernæst er der 30 minutter fra midnat til 00:30.
   Dvs. Sleipner ligger i havnen i 6 timer og 30 min.
   
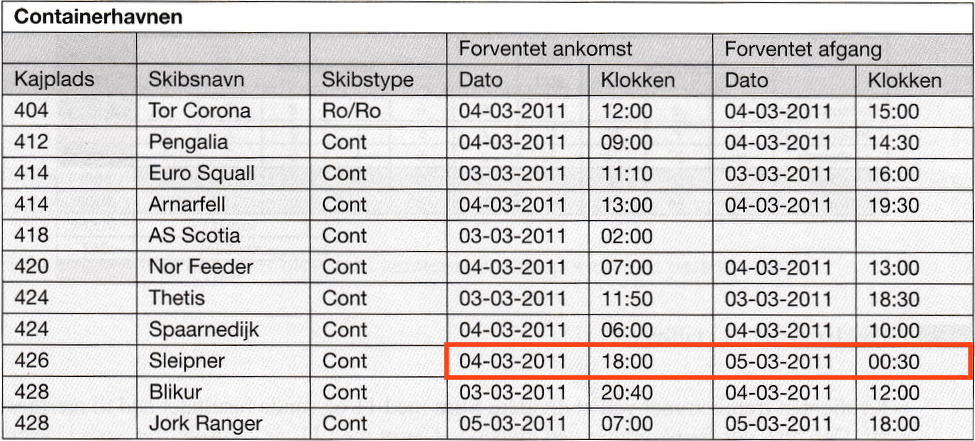
4. Det ses af skemaet at Thetis lå ved kajplads 424 fra kl. 11:50 til 18:30 den 3/3. Spaarnedjik lå ved kajplads 424 fra 06:00 til 10:00 den 4/3.
   
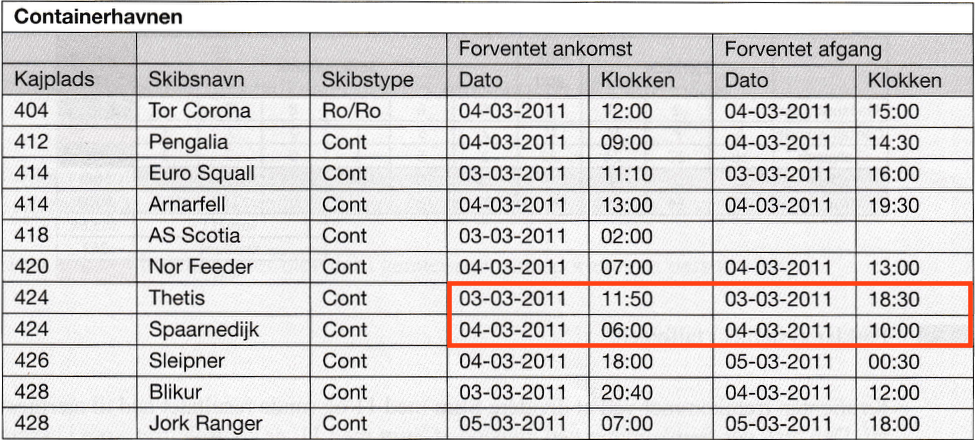
   Thetis lå der i 18 timer og 30 min - 11 timer og 50 min. =
   17 timer og (60 + 30) min. - 11 timer og 50 min. = (man låner en time i minutter)
   17 timer og 90 min. - 11 timer og 50 min. =
   17 timer - 11 timer og (90 min. - 50 min.) =
   6 timer og 40 min.
   Spaarnedjik lå der i 10 timer og 0 min - 6 timer og 0 min. = 4 timer
   Til sammen lå de der i 6 timer og 40 min. + 4 timer = 10 timer og 40 min.
   Det samlede tidsrum er 3 døgn = 3·24 timer = 72 timer. Dermed var kajplads 424 ledig i:
   72 timer - 10 timer og 40 min. =
   71 timer og 60 min. - 10 timer og 40 min. =
   71 timer - 10 timer og (60 min. - 40 min.) =
   61 timer og 20 min = 61 timer og 20·(1/60 time) = 61 + 20/60 timer = 61¹/₃ time.
   Kajplads 424 var dermed ledig i [(61¹/₃)/72]·100 % = 85 % af tiden.

Svar på opgave 5: GPS

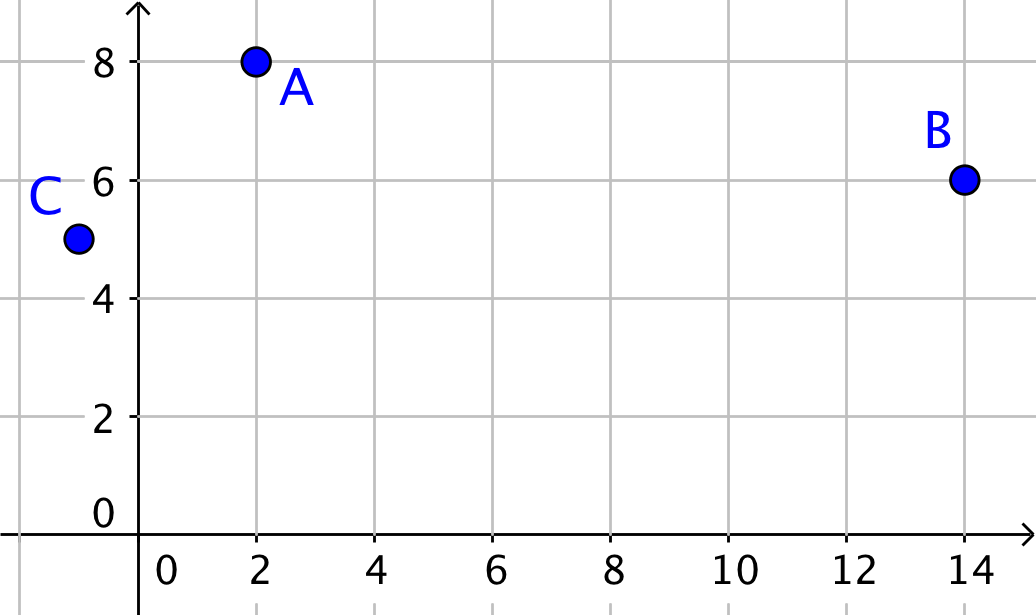
1. Punkterne A, B og C er tegnet ind i et koordinatsystem nedenunder.
   
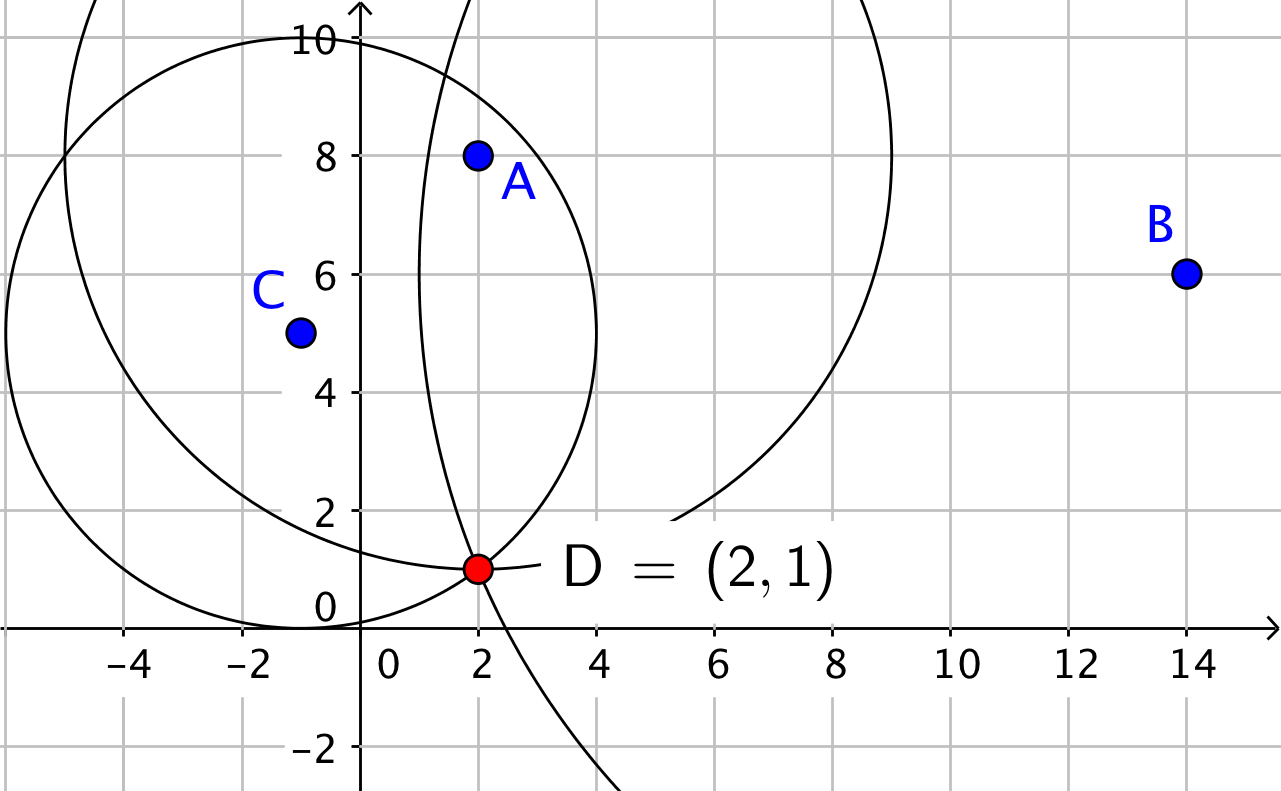
2. Man konstruerer punktet i Geogebra ved at tegne en cirkel med radius 7 og A som centrum, en cirkel med radius 13 og B som centrum samt en cirkel med radius 5 og C som centrum. Disse skærer hinanden i et fælles punkt kaldet D. Koordinaterne til skæringspunktet aflæses til (2,1)
   
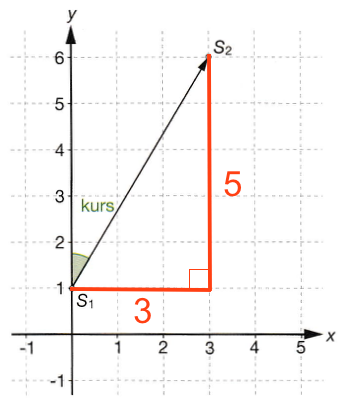
3. Afstanden mellem S₁ og S₂ kan beregnes ved at tegne en retvinklet trekant i koordinatsystemet som vist og bruge Pythagoras læresætning. Afstanden er √[3² + 5²] = √34 = 5,83 enheder.
   
4. Kursen kaldes v. Som vist nedenunder indgår v i en retvinklet trekant med siden S₁S₂ som hypotenusen.
   
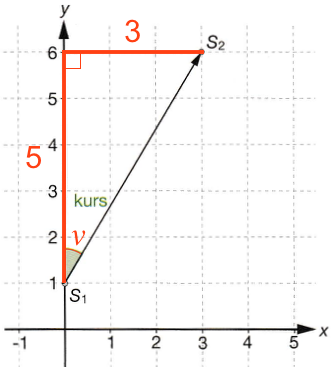
   For en spids vinkel, v, i en retvinklet trekant gælder, at tan(v) er lig med modstående katete divideret med hosliggende katete. Man får:
   tan(v) = 3/5 ⇒
   v = tan^-1(3/5) ⇔
   v = 30,96°
   Dvs. kursen er ca. 31°
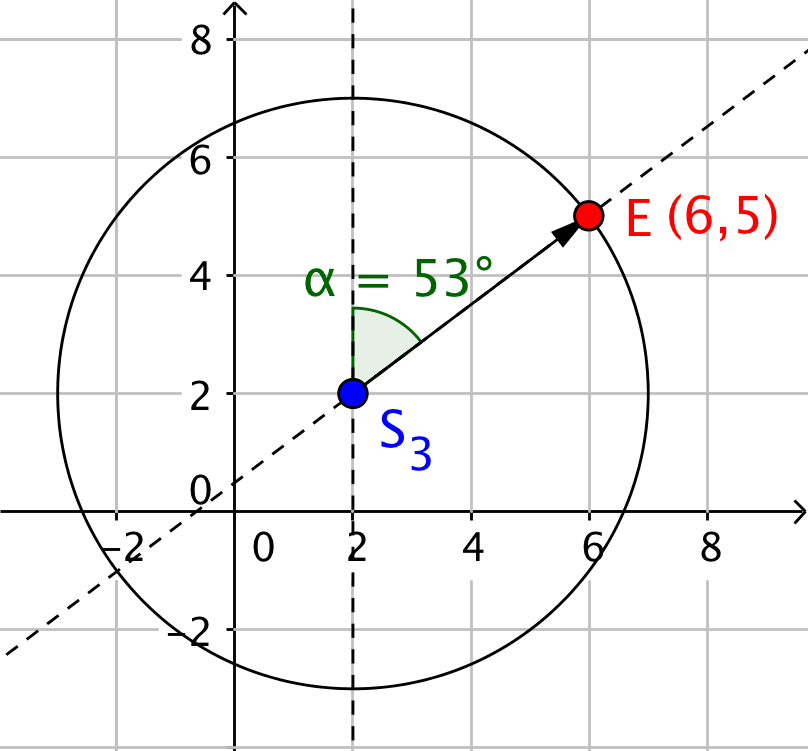
5. På nedenstående tegning er punktet konstrueret som vist. Man drejer en lodret linje 53° med uret og afsætter afstanden 5 enheder ved hjælp af cirkel-værktøjet. Der hvor cirklen skærer den drejede linje ligger punktet (kaldet E). Punktet har som vist koordinaterne (6,5)