Svar på opgave 1: Randers regnskov

1. Radius er (50 m)/2 = 25 m
2. Arealet af gulvet er π·(25 m)² = 1964 m²
3. Kuplens rumfang er halvdelen af rumfaget af en kugle med radius 25 m. Dvs. rumfanget af kuplen er
   0,5·(4/3)·π·(25 m)³ = 32724 m³ ≈ 33000 m³
4. Kuplens samlede overflade er halvdelen af overfladen af en kugle med radius 25 m. Dvs. overfladen af kuplen er 0,5·4·π·(25 m)² = 3926,99 m²
   Dvs. andelen af glas i kuplen er [(2827 m²)/(3926,99 m²)]·100 % = 72 %
5. Forskellen mellem det årlige varmeforbrug pr. m² i Randers regnskov og et parcelhus er 320 kWh - 85 kWh = 235 kWh
6. Varmeforbruget i Sydamerikakuplen pr. m³ er (1050000/33000) kWh/m³ = 31,82 kWh/m³
   Varmeforbruget i et parcelhus med gulvarealet 150 m² er 150 m²·85 kWh = 12750 kWh. Varmeforbruget pr, m³ er derfor: 12750/360 kWh/m³ = 35,42 kWh/m³
   Dvs. varmeforbruget pr. m³ er mindre i Sydamerikakuplen end i et parcelhus.

Svar på opgave 2: Mad til to søkøer

1. Hver søko spiser om dagen: 0,5·(15 + 5 + 5 + 5) kg = 15 kg
2. Man omregner først kostens energiindhold til kJ/kg:
   Salat: 92 kJ/100 g = 92 kJ/0,1 kg = 920 kJ/kg
   Kål: 126 kJ/100 g = 1260 kJ/kg
   Majs: 386 kJ/100 g = 3860 kJ/kg
   Gulerødder: 151 kJ/100 g = 1510 kJ/kg
   Energiindholdet i en søkos kost er: 0,5·(15·920 + 5·1260 + 5·3860 + 5·1510) kJ/kg = 23475 kJ/kg
3. Kurven er tegnet i Geogebra:
   
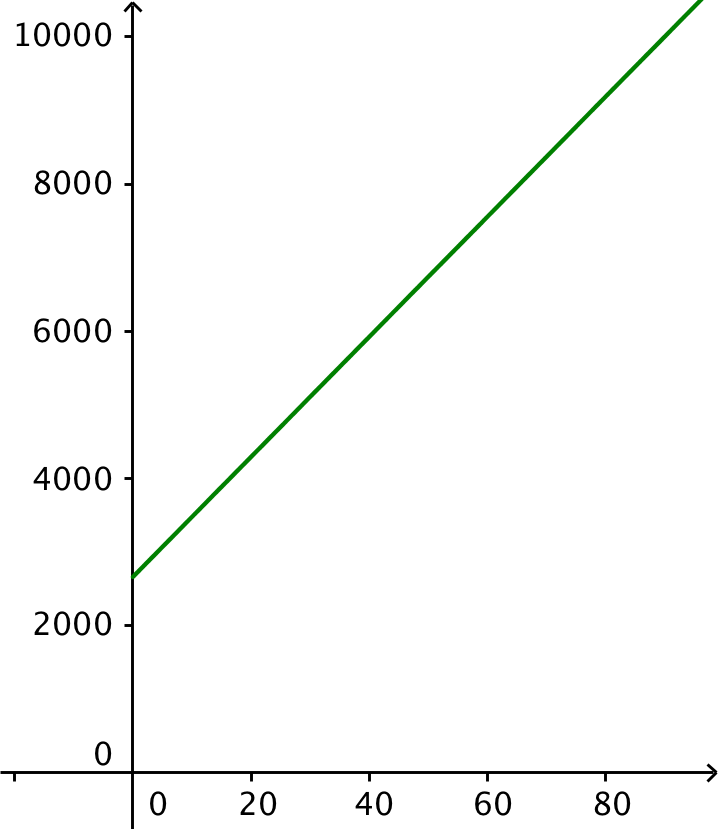
4. Det daglige energiforbrug for en 16-årig på 60 kg findes ved at indsætte x = 60 i formlen for energiforbruget:
   81,5·60 + 2664 kJ = 7554 kJ
5. Hvis man spiser 100 g af hver fødevare får man et dagligt energitilskud på (92 + 126 + 386 + 151) kJ = 755 kJ. Dividerer man dette op i 7800 kJ får man 10,3. Dvs hun skal spise (100 g)·10,3 = 1,03 kg af hver fødevare.

Svar på opgave 3: Bordene i skoletjenesten

1. Tegnet nedenunder i Geogebra i forholdet ca. 1:30. (Et rigtigt målestoksforhold kræver en papirtegning.)
   
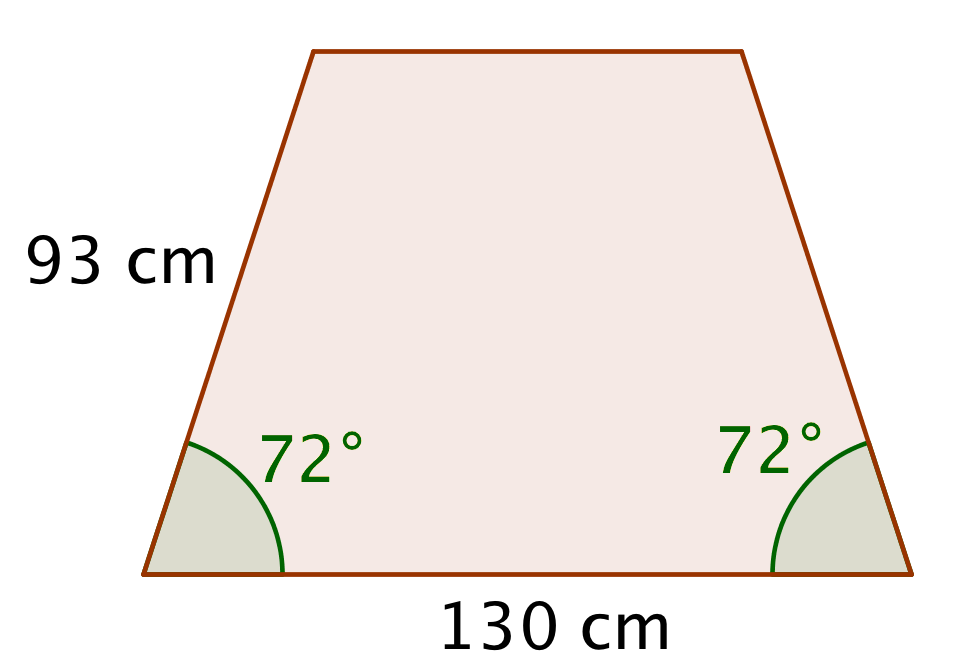
2. Summen af vinklerne i en firkant er 360°. De to vinkler på 72° giver sammenlagt 144°. De to resterende vinkler er derfor hver (360° - 144°)/2 = 108°
3. Højden findes ved hjælp af den trigonometriske formel: højde = (93 cm)·sin(72°) = 88,4 cm
4. Den korte og den lange side på hver trapez går ud i et og danner et ret linjestykke, idet de to vinkler, der ligger ved siden af hinanden, tilsammen er 180°. Den firkant man får ud af det har lige store modstående sider og er dermed et parallelogram. Tegnet i Geogebra:
   
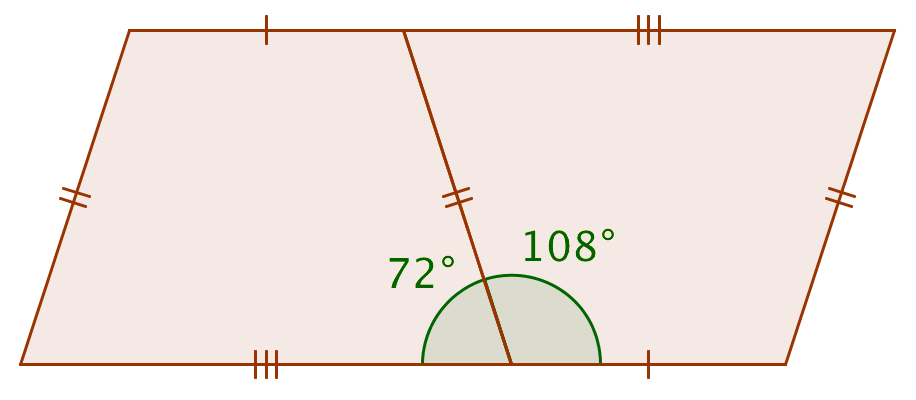
5. Man kan sætte bordene sammen i en ring, der har form som en regulær 10-kant.
   

Svar på opgave 4: Verde Sumaco

1. De går hjemmefra kl. 5. De forlader skolen kl. 12 og er hjemme 12 + 2,5 timer = 14:30. Mellem kl. 5:00 og kl. 14:30 er der 9 timer og 30 minutter, som er den tid, der går fra de tager hjemmefra til de er tilbage igen.
2. Arealet af Verde Sumaco er 18.456 ha = 18.456·(1 ha) = 18.456·(0,01 km²) = 185 km²
3. Forholdet mellem arealerne af Bornholm og Verde Sumaco er 185/588 = 1/(3,18) eller ca. 1:3
4. Antal mænd i Verde Sumaco: 65 + 39 + 35 + 13 + 6 + 7 + 1 + 2 = 167
   Antal kvinder i Verde Sumaco: 35 + 33 + 16 + 13 + 8 + 7 + 1 = 113
   Antal mennesker i Verde Sumaco: 167 + 113 = 280
   Dette giver den gennemsnitlige familiestørrelse: 280/49 ≈ 6
5. Befolkningstætheden i Verde Sumaco er 280/185 pr. km² = 1,5 pr. km².
   Befolkningstætheden på Bornholm er (42066/588) pr. km² = 71,5 pr. km².
   Forskellen er forholdsmæssigt: 71,5/1,5 = 47,7 ≈ 50,
   dvs. der er 50 gange så stor en befolkningstæthed på Bornholm som på Verde Sumaco.
6. Andelen af befolkningen i aldersgruppen 0-10 år er [(64 + 35)/280]·100 % = 35 %
   Andelen af befolkningen i aldersgruppen 31-40 år er [(13 + 13)/280]·100 % = 9,2 %
7. Et pindediagram over aldersammensætningen i % er vist nedenunder lavet i Excel.
   
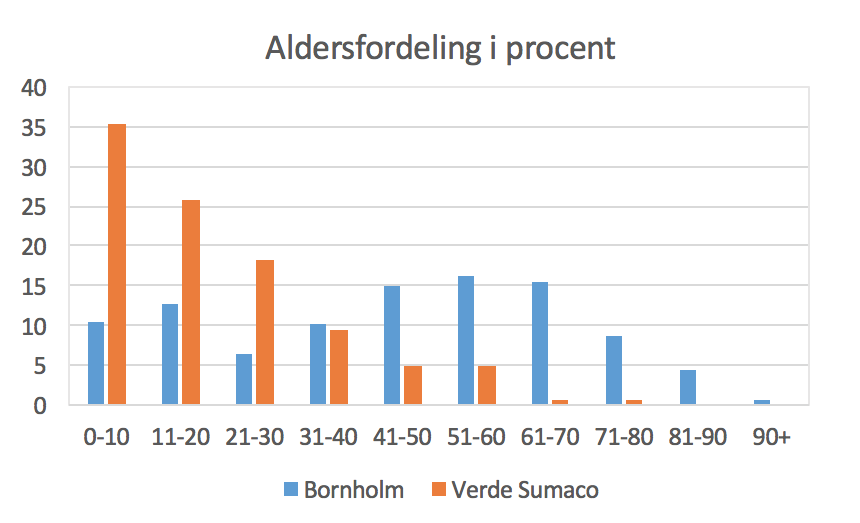
8. Befolkningen i Verde Sumaco består overvejende af børn, mens befolkningssammensætningen på Bornholm er mere ensartet, dvs. der er nogenlunde lige mange % af hver aldergruppe på nær de ældste.
9. Forslag b) og c) er rigtige. Forslag a) ville være rigtigt, hvis man sagde 13 procentpoint i stedet for 13 %.
   b) er rigtig, fordi man skal tage forholdet mellem 26 % og 13 % og her er 26 dobbelt så stort som 13 eller 100 % større. c) er rigtig for, hvis man går den modsatte vej, er 13 halvt så stort som 26 eller 50 % mindre. (Noget der er 100 % mindre end noget andet er altid lig med 0.)

Svar på opgave 5: Kombinatorik og sandsynlighed

1. Når en sandsynlighed enten det ene eller det andet skal sandsynlighederne for hver lægges sammen (med mindre noget kan være både og, men det er ikke tilfældet her).
   Man får sandsynligheden for højre side eller venstre side til: 1/3 + 1/3 = 2/3 = 67 %
2. Sandsynlighederne i tabellen dækker alle tænkelige muligheder af et kast og sandsynlighederne for de enkelte muligheder skal derfor give 1 tilsammen.
   Summen af tallene i tabellen er 1/10 + 1/3 + 1/3 + 1/5 = 29/30.
   Dette trækkes fra 1: 1 - 29/30 = 1/30 = 3,3 %,
   som er sandsynligheden for snude.
3. B = Ben, H = Højre, V = Venstre, R = Ryg, S = Snude. Kombinationerne er
   (Rød B, Blå B); (Rød B, Blå H); (Rød B, Blå V); (Rød B, Blå R); (Rød B, Blå S);
   (Rød H, Blå B); (Rød H, Blå H); (Rød H, Blå V); (Rød H, Blå R); (Rød H, Blå S);
   (Rød V, Blå B); (Rød V, Blå H); (Rød V, Blå V); (Rød V, Blå R); (Rød V, Blå S);
   (Rød R, Blå B); (Rød R, Blå H); (Rød R, Blå V); (Rød R, Blå R); (Rød R, Blå S);
   (Rød S, Blå B); (Rød S, Blå H); (Rød S, Blå V); (Rød S, Blå R); (Rød S, Blå S).
4. Når man skal finde sandsynligheden for at to tilfælde optræder samtidig (blå ryg samtidig med rød venstre) skal man gange sandsynlighederne for hvert tilfælde.
   Dvs. sandsynligheden for (Blå R, Rød V) er (1/3)·(1/5) = 1/15 = 6,7 %
5. Sandsynligheden for hver kombination findes ved at gange, fordi der er tale om noget der skal ske på en gang. De tal som man ganger er parvis ens, fordi sandsynligheden for ben, venstre...osv. er ens for blå og rød kat. Sandsynlighderne for hver kombination er:
   (Rød B, Blå B) = (1/10)·(1/10) = (1/10)²
   (Rød V, Blå V) = (1/3)·(1/3) = (1/3)²
   (Rød H, Blå H) = (1/3)·(1/3) = (1/3)²
   (Rød R, Blå R) = (1/5)·(1/5) = (1/5)²
   (Rød S, Blå S) = (1/30)·(1/30) = (1/30)²
   Disse tal skal lægges sammen, da man ser på enten den ene, den anden...osv. kombination.
   Summen er (1/10)² + (1/3)² + (1/3)² + (1/5)² + (1/30)² =
   41/150 = 27,3 %