Svar på opgave 1: Laura er murer - fliser på badeværelset

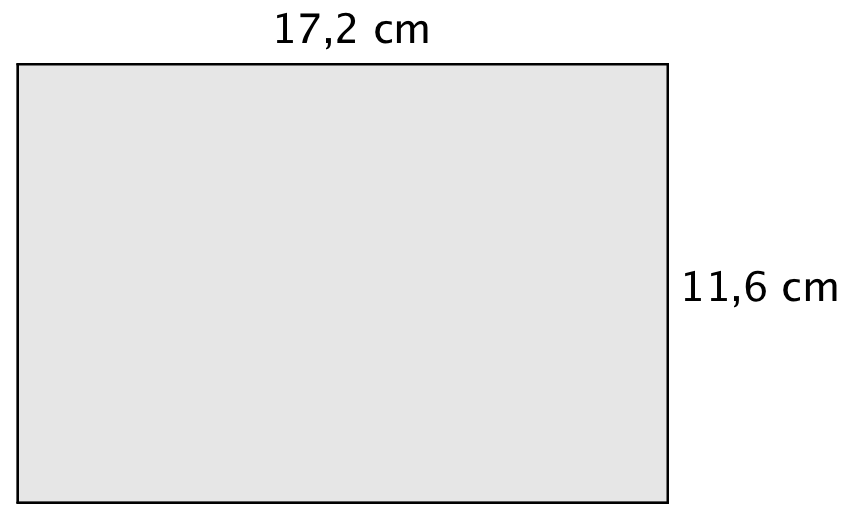
1. Grundplanen er tegnet nedenunder med gråt. Tallene henviser til mål på papiret.
   
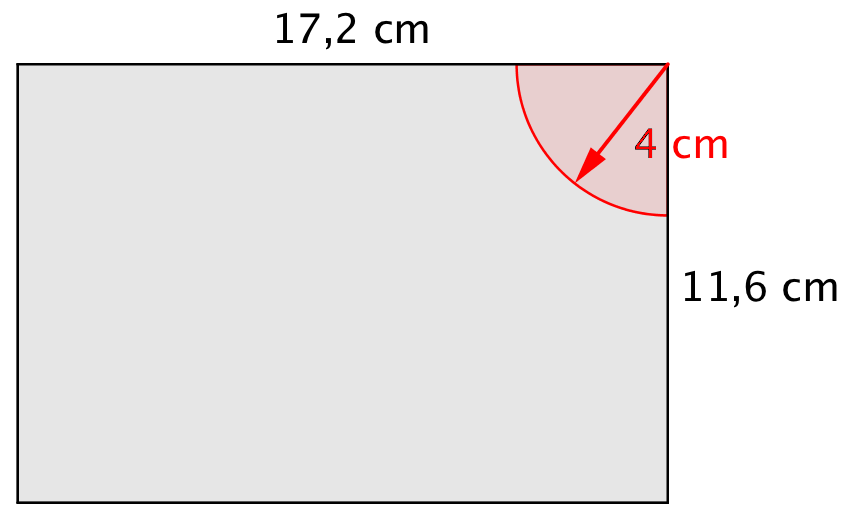
2. Brusenichen er vist med rødt på grundplanen nedenunder.
   
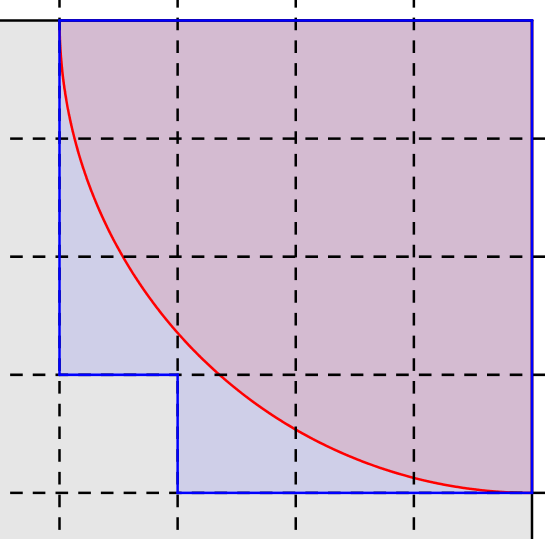
3. Nedenunder er brusenichen forstørret op med fliserne vist som stiplede linjer.
   Under forudsætning af, at man enten bruger hele fliser eller fliser, som er skåret til efter cirkelbuen, så skal der brugers 15 fliser. Dette er vist med den blå polygon.
   Under forudsætning af at man må dele hver flise i så mange stykker som man har lyst og lægge dem sammen, som man har lyst, skal der bruges 12,6 fliser. Dette finder man ved at dividere en flises areal op i brusenichens areal: (areal af bruseniche)/(areal af flise) = [(1/4)·π·(1 m)²]/(0,25 m)² = 12,6 gange.
   
4. Arealet af gulvet er (2,90 m)·(4,30 m) - (1/4)·π·(1 m)² = 2,90·4,30 m² - (1/4)·π m² = 12,47 m² - 0,785 m² = 11,685 m²
   Antallet af kasser er (11,685 m²)/(2,4 m²/kasse) = 4,87 kasser.
   Dette rundes op til 5 kasser, som er det antal kasser med fliser, der skal bruges.
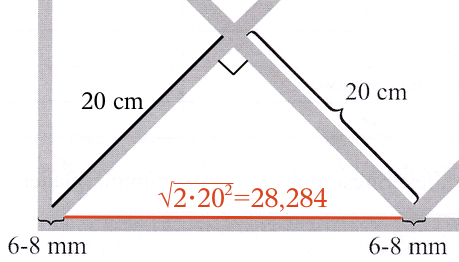
5. En flise, der er halveret langs diagonalen, er en retvinklet ligebenet trekant. Diagonalens længde findes ved hjælp af Pythagoras læresætning.
   Dette giver: (20 cm)² + (20 cm)² = diagonal² ⇒ diagonal = √[20² + 20²] cm = 28,284 cm.
   Man antager, at fugebredden er 0,7 cm. Antallet af fliser kaldes x. Der er en fuge mere end antallet af fliser. Man skal løse ligningen:
   x·28,28 + (x + 1)·0,7 = 290 ⇔
   x·28,28 + 0,7·x + 0,7 = 290 ⇔
   x·28,98 = 290 - 0,7 ⇔
   x·28,98 = 289,3 ⇔
   x = 289,3/28,98 ⇔
   x = 9,98
   Dvs. der skal bruges 10 afskårne fliser
   
6. Gulvets areal inklusive bruseniche er (2,90 m)·(4,30 m) = 12,47 m². Mængden af fugemasse er dermed:
   (12,47 m²)·(2,9 kg/m²) = 36,2 kg
7. 25 kg poserner er billigere pr. kg end 5 kg poserne. Derfor kan det ikke betale sig udelukkende at købe 5 kg poser, hvis vægten af klæbemasse er over 25 kg.
   Det billigeste må derfor enten være kun at købe 25 kg poser eller så mange 25-kg poser, man kan uden at komme over 36 kg og derefter lade resten være 5-kg poser.
   Der skal to 25 kg koser til at give over 36,2 kg. Disse poser koster: 2·114 kr = 228 kr.
   Hvis man nøjes med een 25 kg pose, så skal man lægge tre 5-kilo poser til for at få over 36,2 kg. Dette koster 114 kr. + 3·(39 kr.) = 231 kr.
   Dvs. 2 stk. 25-kilo poser er billigst.

Svar på opgave 2: Kristian er bilforhandler - salg af bil

1. Det samlede beløb på slutsedlen er (276.997 + 4.746 + 8.036 + 3.866 + 2.400 + 1.180) kr. = 297.225 kr.
2. Man har: lån = [kontantbeløb - (kontant udbetaling)] + låneomkostning = [restkøbesum] + låneomkostning.
   Dvs. kunden skal låne: 297.225 kr. - (297.225 kr.)·(20 %) + 5.000 kr. = 242.780 kr.
3. Kunden skal betale i følgende antal måneder: 7 år = 7·(1 år) = 7·(12 mdr.) = 7·12 mdr. = 84 mdr.
4. Ydelsen er: (242.780·0,005)/(1 - (1 + 0,005)^-84) kr. =
   (242.780·0,005)/(1 - 1,005^-84) kr. =
   (1213,9/0,342265) kr. =
   3.546,67 kr. = 3.547 kr.
5. Det samlede beløb, som kunden skal betale er: kontant udbetaling + låneomkostning + lån =
   kontant udbetaling + låneomkostning + (antal terminer eller måneder)·(månedlig ydelse) =
   (297.225 kr.)·(20 %) + 5.000 kr. + 84·(3.546,67 kr.) =
   (297.225·20 % + 5.000 + 84·3.546,67) kr. =
   362.365 kr.
6. Salgspriserne er indrammet på skemaet nedenunder.
   Forskellen er (287.498 - 262.498) kr. = 25.000 kr.
   
7. Årlige omkostninger = udgift til brændstof + ejerafgift. Det bemærkes, at ejerafgiften skal betales hvert halvår.
   Udgift til brændstof beregnes på følgende måde: [(antal kørte km)/(antal L brændstof/km)]·(pris for brændstof/km)
   For benzinbilen får man den årlige udgift: ((20000/19.2)·10,5 + 2·510) kr. = 11.957,50 kr.
   For dieselbilen får man: ((20000/24,4)·9,1 + 2·980) kr. = 9.419,02 kr.
   Forskellen på årlig udgift mellem de to biler er (11.957,50 - 9.419,02) kr. = 2.538,48 kr. ≈ 2.500 kr.
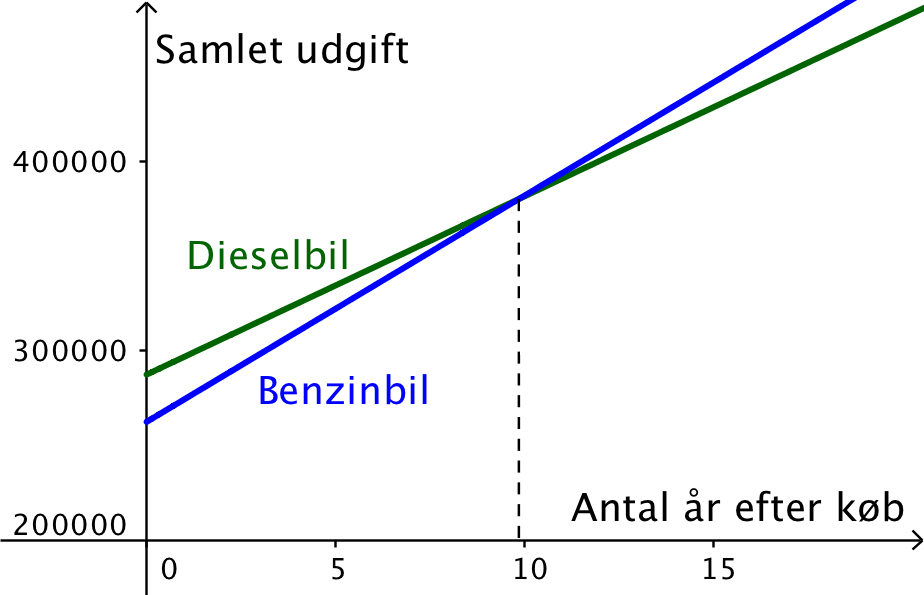
8. Nedenunder er vist et forslag til en grafisk sammenligning af udgifterne til de to biler. Bemærk at x-aksen skærer y-aksen for y = 200.000.
   Den grønne linje viser asmlet udgift for dieselbilen og linjen har ligningen y = 287.498 + 9.419,02·x. Den blå linje viser udviklingen i den samlede udgift til benzinbilen. Denne linje har ligningen y = 262.498 + 11.957,50·x.
   Den stiplede lodrette linje viser, at skæringen mellem udgifterne er ved ca. 10 år.
   
9. Hvis bilerne kører mere end 20.000 km om året, vil benzinbilen blive dyrere end dieselbilen på kortere tid end de ti år, der gælder, hvis man kører 20.000 km om året.
   Dette skyldes, at brændstofudgiften pr. kørt km er større for benzinbilen end for dieselbilen.
   For benzinbilen er brændstofudgiften pr. kørt km: (10,5 kr./L)/(19,1 km/L) = 0,55 kr./km
   For dieselbilen er brændstofudgiften pr. kørt km: (9,10 kr./L)/(24,4 km/L) = 0,37 kr./km
   (Det er ikke hele forklaringen. Den ville kræve, at man fandt en formel for skæringspunktet mellem de to linjer. Det kan vises, at kører man under 5404 km/år, vil dieselbilen altid være dyrest på grund af dens høje ejerafgift.)
   Nedenunder er vist en interaktiv graf lavet i Geogebra. Den røde skyder bruges til at ændre antal kørte km om året. Den stiplede linje viser, hvornår graferne skærer hinanden.
   
   (Se evt. grafen på Geogebra's hjemmeside).

Svar på opgave 3: Kosmetolog - egen klinik

1. Omsætning uden moms kaldes x. Der gælder at x + x·moms = omsætning med moms. Det giver her:
   x + x·(25 %) = 42.300 kr. ⇔
   x·(1 + 25 %) = 42.300 kr. ⇔
   x·1,25 = 42.300 kr. ⇔
   x = (42.300 kr.)/1,25 ⇔
   x = 33.840 kr.
   Dvs. omsætning uden moms er 33.840 kr.
2. Løn = (omsætning uden moms) - (udgifter uden moms) =
   33.840 kr. - (950 + 6500 + 650 + 630 + 370 + 280) kr. =
   33.840 kr. - 9.380 kr. = 24.460 kr.
3. Man kalder omsætningen med moms for x. Udgifterne forudsættes at være de samme som i forrige spørgsmål.
   Sammenhængen mellem omsætning med og omsætning uden moms kan skrives: (omsætning uden moms) = (omsætning med moms)/1,25, dvs.: omsætning uden moms = x/1,25. Dette giver følgende ligning med hensyn til x:
   løn = (omsætning uden moms) - (udgifter uden moms) ⇒
   25.000 kr. = x/1,25 - 9.380 kr. ⇒
   34.380 kr. = x/1,25 ⇒
   x = (34.380 kr.)·1,25 ⇒
   x = 42.975 kr.
   Dvs. Sofie skulle have haft en omsætning med moms på 42.975 kr. i november for at have haft en løn på 25.000 kr.
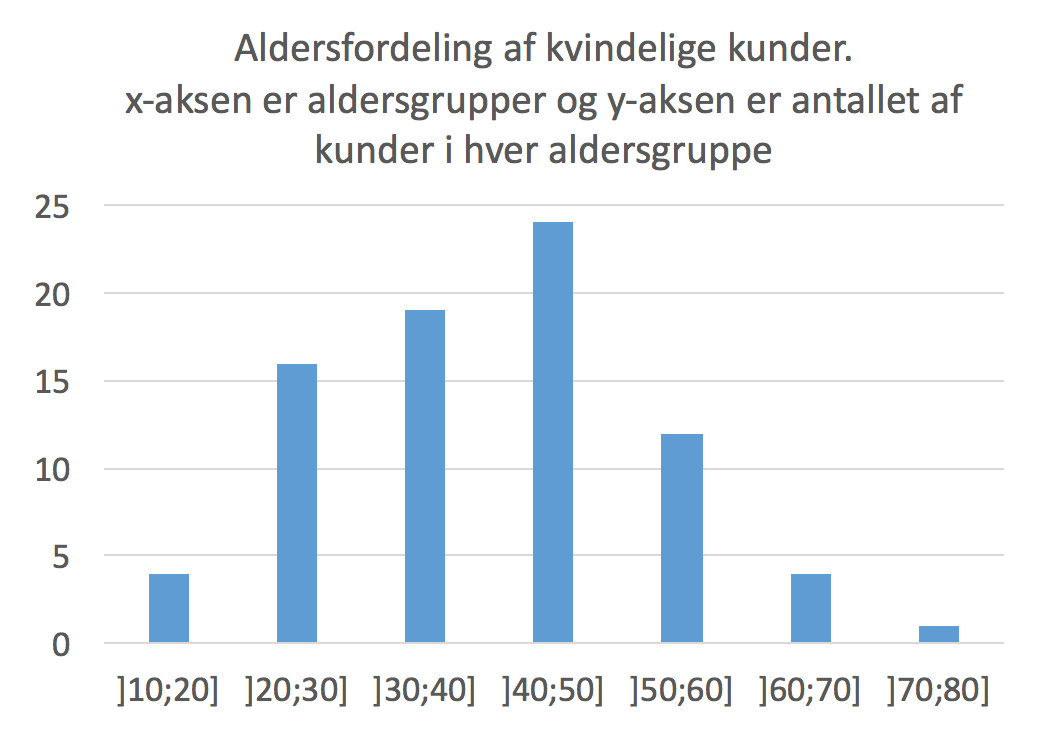
4. Nedenfor er vist et søjle- eller pindediagram lavet i Excel.
   
5. Variationsbredden for kvinder: 80 år - 10 år = 70 år
   Variationsbredden for mænd: 50 år - 20 år = 30 år
   Middeltal for kvinder: (4·15 + 16·25 + 19·35 + 24·45 + 12·55 + 4·65 + 1·75)/(4+ 16 + 19 + 24 + 12 + 4 + 1) år = 40 år
   Middeltal for mænd: (3·25 + 5·35 + 14·45)/(3 + 5 + 14) år = 40 år
   Dvs. at variationsbredden er størst for kvinder, mens middeltallet er det samme

Svar på opgave 4: Tømrer - tagkonstruktion

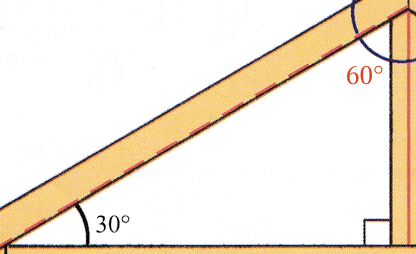
1. Det fremgår af tegningen, at vinklerne u og v danner en ret linje, dvs. u + v = 180°.
   
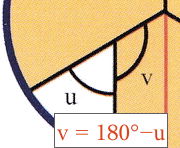
   Desuden ses det, at u er den tredje vinkel i en trekant, hvor de andre vinkler er 30° og 90°.
   Da summen af vinklerne i en trekant er 180° får man, at u = 180° - 30° - 90° = 60°
   Dermed er v = 180° - 60° = 120°
   
2. Den lodrette side indgår i en trekant som nedenunder er kaldt ABC.
   
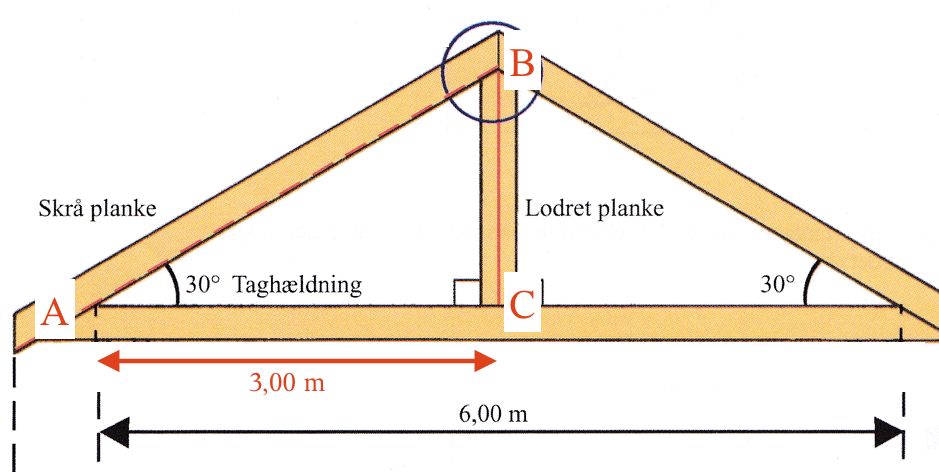
   Det ses, at |AC| er halvdelen af 6,00 m, dvs. |AC| = 3,00 m. Man skal finde |BC|. Da trekant ABC er retvinklet, så gælder den trigonometriske ligning:
   tan(A) = |BC|/|AC| ⇒
   tan(30°) = |BC|/3,00 m ⇔
   1/√3 = |BC|/3,00 m ⇒
   |BC| = (3,00 m)·(1/√3) = 1,73205 m
   Dvs. længden af det lodrette stykke er ca. 1,73 m
3. Den stiplede linje er hypotenusen i en ny retvinklet trekant, der er vist nedenunder.
   
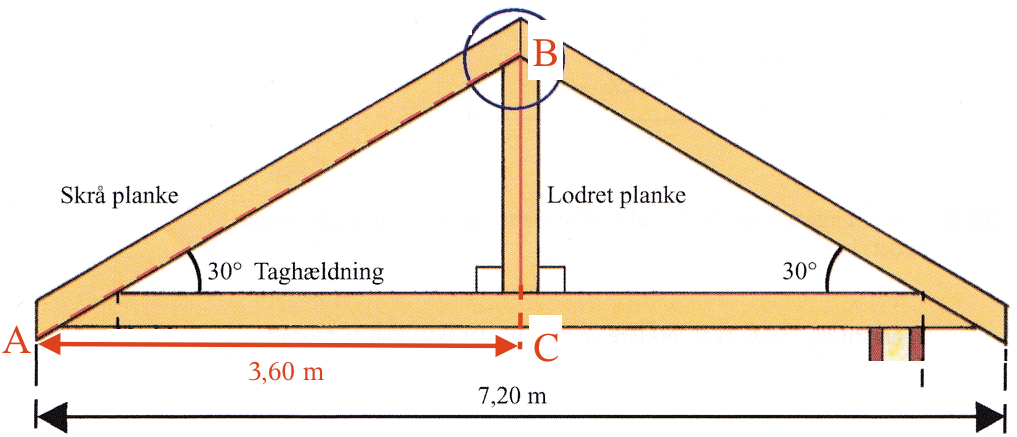
   Her ses det at |AC| = 3,60 m. Man kender derimod ikke |BC|.
   Man kan ikke bruge samme formel som før og heller ikke Pythagoras' læresætning.
   Man kan derinmod bruge formlen:
   |AB|·cos(A) = |AC| (hypotenuse gange cosinus er lig med hosliggende katete) ⇒
   |AB|·cos(30°) = 3,60 m ⇔
   |AB|·(√3/2) = 3,60 m ⇔
   |AB| = (2/√3)·3,60 m ⇔
   |AB| = 4,16 m
   Dvs. længden af det skrå spær er 4,16 m
4. Nedenstående tegning viser et hus med de nævnte mål.
   

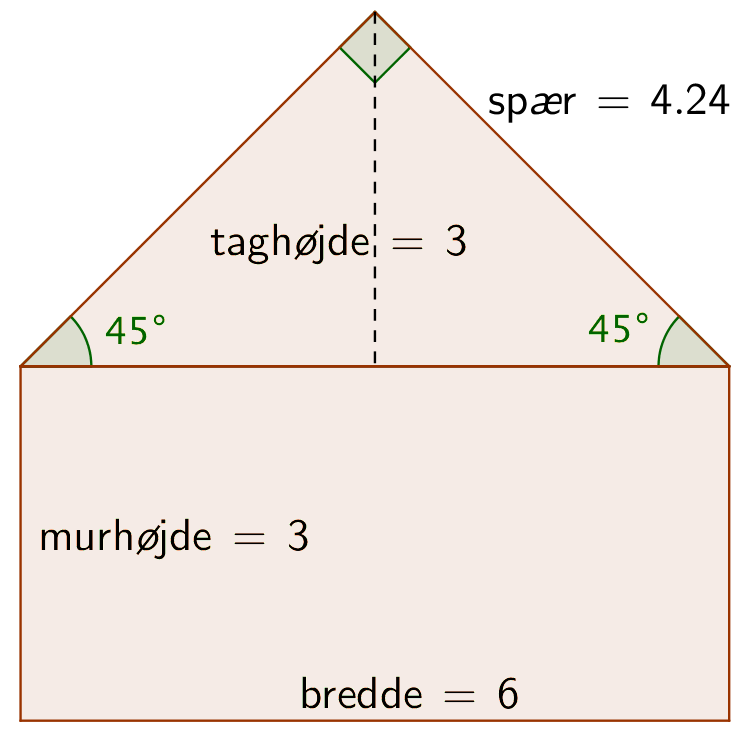
Svar på opgave 5: Beskrivelse af et mønster

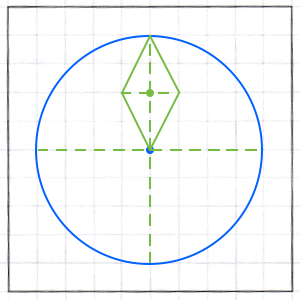
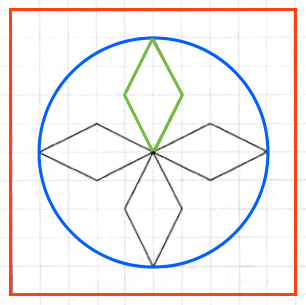
1. Figuren består af et rødt kvadrat med en blå cirkel indeni. I cirklen er fire romber. Romberne er drejet omkring cirklens centrum med 90° mellem hver og danner en roset.
   
2. Der er givet et kvadrat med siden 10, som er tegnet på et kvadratnet, hvor det enkelte kvadrat i nette har siden 1. Man bruger diagonalernes skæringspunkt for det store kvadrat som centrum for en cirkel med radius 4. Dette er vist nedenunder.
   
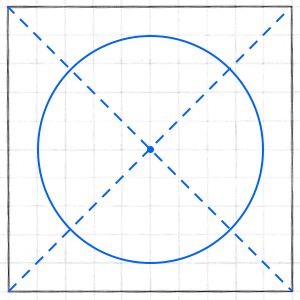
   Der tegnes to diametre til cirklen. De står vinkelret på hinanden, den ene lodret den anden vandret. Dette giver fire radier til cirklen. Ud fra hver radius tegnes en rombe som vist nedenunder.
   Rombens længste diagonal er radius af cirklen og den korte diagonal har længden 2.