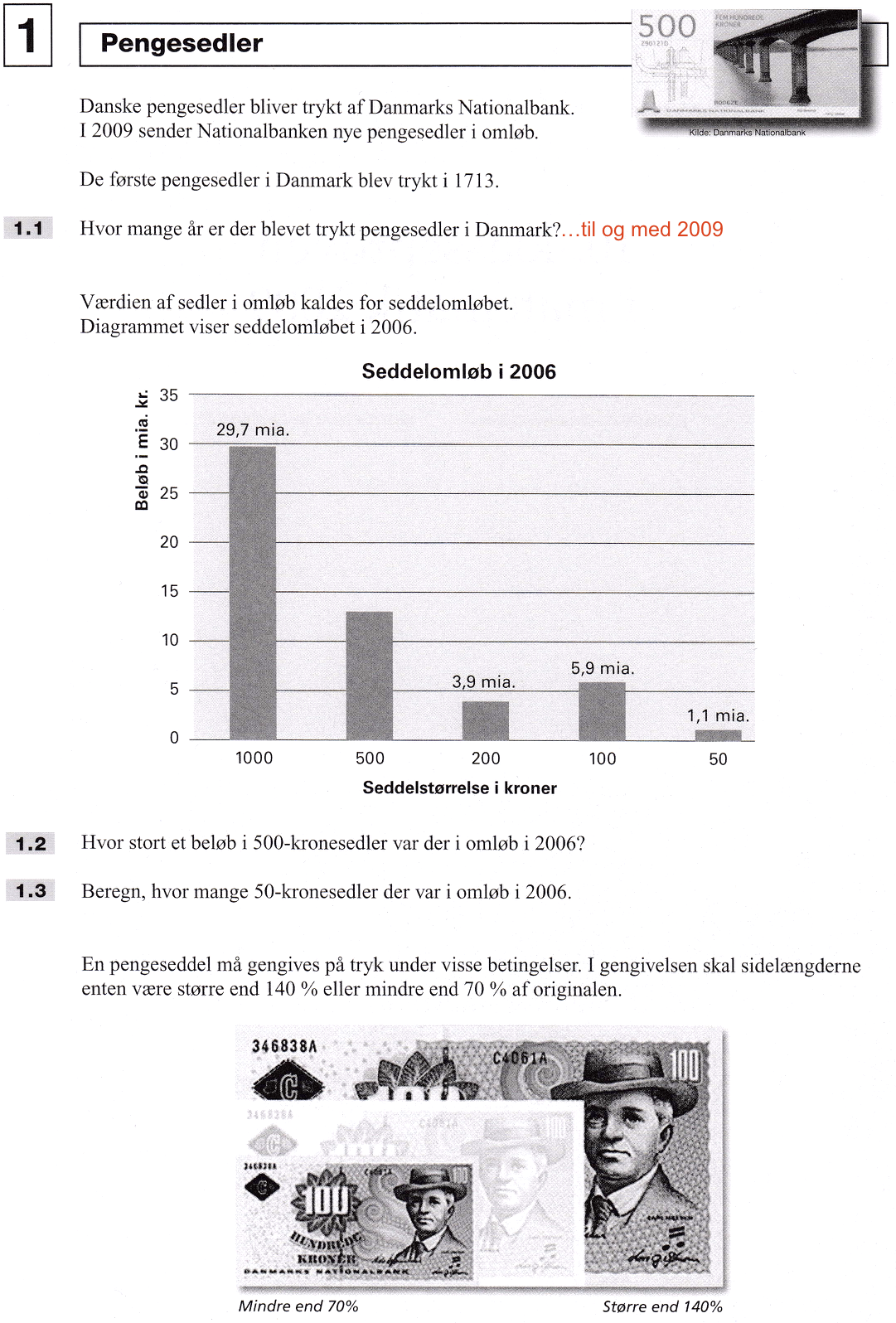
Svar på opgave 1: Pengesedler

1. Antal år = 2009 - 1713 år = 296 år

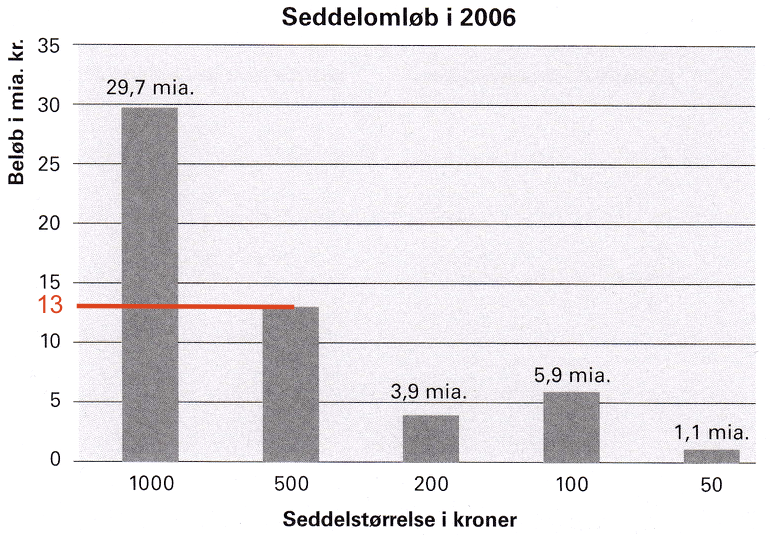
2. Beløbet aflæses til 13 mia kr.

   

3. Man ved at antal sedler gange pålydende skal være lig med samlet værdi. Idet antal sedler kaldes x, får man ligningen:

   x·50 kr. = 1,1 mia kr. ⇒ x = (1100 mio kr.)/(50 kr.) = 22 mio.

   Dvs. antallet af 50 kronesedler = 22 mio.

4. En seddel, der er større end naturlig størrelse, skal mindst have længden (140 %)·(135 mm) = 189 mm og bredden (140 %)·(72 mm) = 100,8 mm.

   Dvs. sedlen er stor nok

5. Der er plads til 2 i bredden. I længden er der plads til 2·(6800 m)/(72 mm) = 2·(6800 m)/(72·0,001 m) = 2·6.800.000/72 = 188.888.

   Dvs., der er plads til 188.888 sedler

6. Arealet af papiret i en rulle er (6800 m)·(32 cm) = (6800 m)·(32·0,01 m) = 68·32 m² = 2176 m².

   Dette vejer 2176 m²·(85 g/m²) = 2176·85 g = 184960 g = 184,96 kg

7. En kasse indeholder 10·100.000 kr. = 1.000.000 kr. På en palle kan der være 10·8 = 80 kasser.

   Det samlede beløb, der kan være på en palle er 80·1.000.000 kr. = 80 mio. kr.

Svar på opgave 2: Mønter

1. En-kronens radius er (20,15 mm)/2 = 10,125 mm

2. En-kronen er cylinderformet med et cylinderformet hul. Rumfanget er (10,125 mm)²·π·(1,6 mm) - (2,05 mm)²·π·(1,6 mm) = 494,176 mm³ = 494,176·(0,1 cm)³ = 0,494 cm³

3. Antal gram kobber er (3,6 g)·(75 %) = 3,6·0,75 g = 2,7 g

4. Pris for kobber: (3,6 g)·0,75·(4 øre) = 10,8 øre

   Pris for nikkel: (3,6 g)·0,25·(12 øre) = 10,8 øre

   Pris for metal i alt: 10,8 øre + 10,8 øre = 21,6 øre

5. Kgl. mønt fremstiller pr. dag følgende antal mønter:

   (700 mønter/min.)·(5 timer/dag) =

   (700 mønter/min.)·(5·60 min./dag) =

   700·5·60 mønter/dag = 210000 mønter/dag

   Fremstillingen af 15.000.000 mønter tager følgende antal dage:

   15.000.000/210.000 dage = 71,4 dage

6. Højden af stablen er (2,35 mm/stk.)·110.500.000 stk. =

   (2,35·0,000001 km/stk.)·110.500.000 stk. = 2,35·0,000001·110.500.000 km =

   2,35·110,5 km = 260 km. Dvs. stablen er højere end Mt. Everest

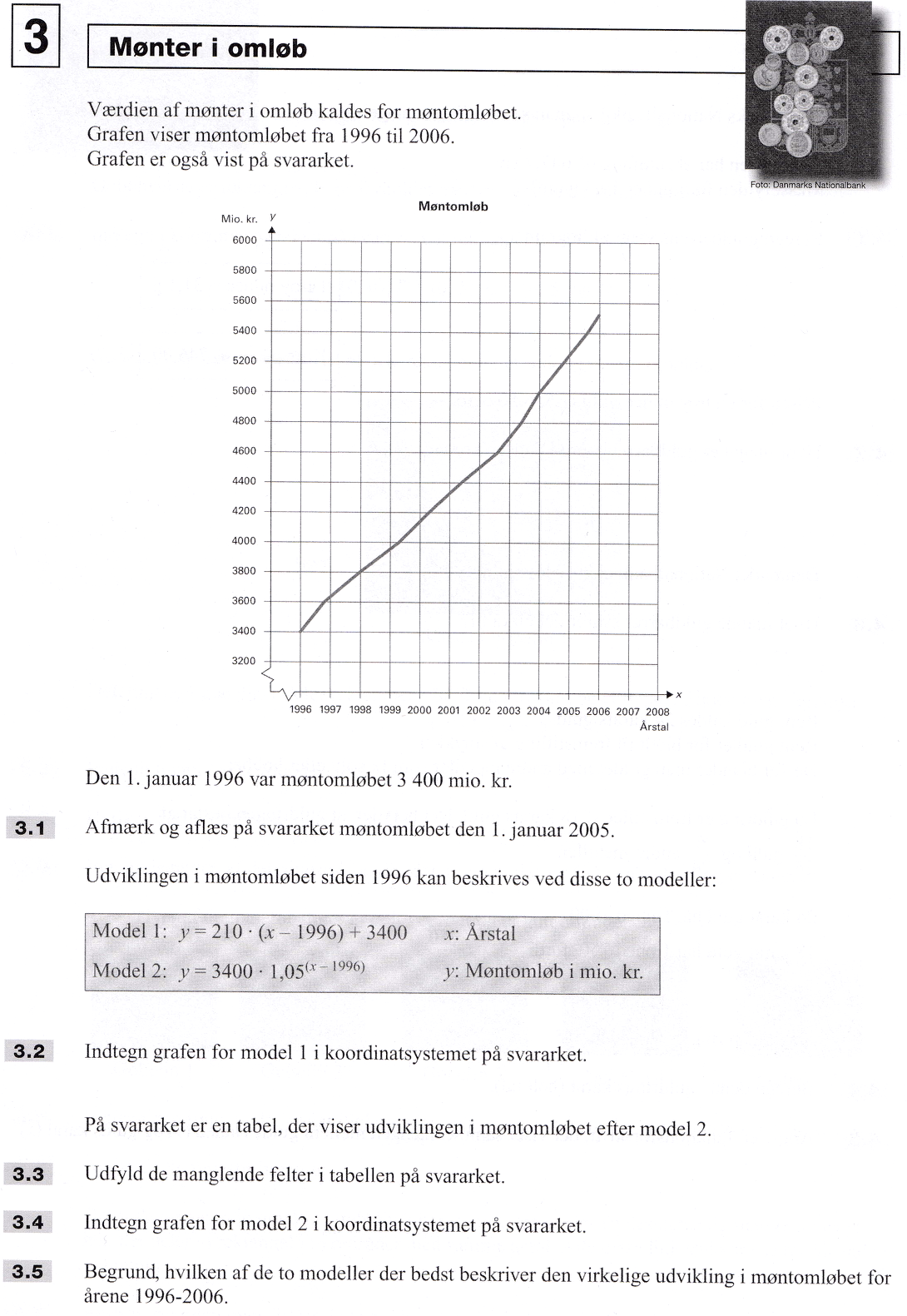
Svar på opgave 3: Mønter i omløb

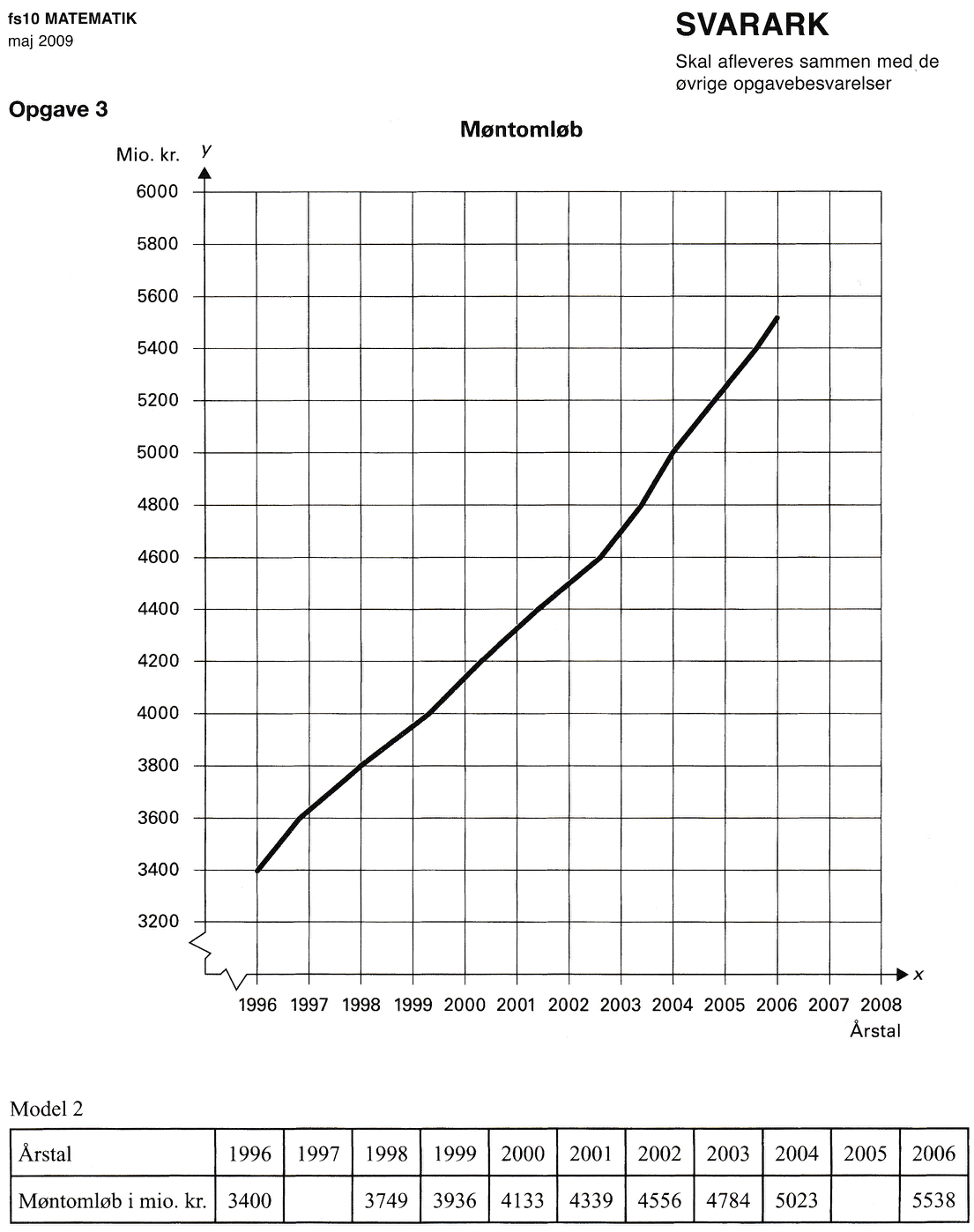
1. Møntomløbet den 1. januar 2005 aflæses (som vist nedenunder) til 5250 mio kr. = 5,25 mia kr.

   

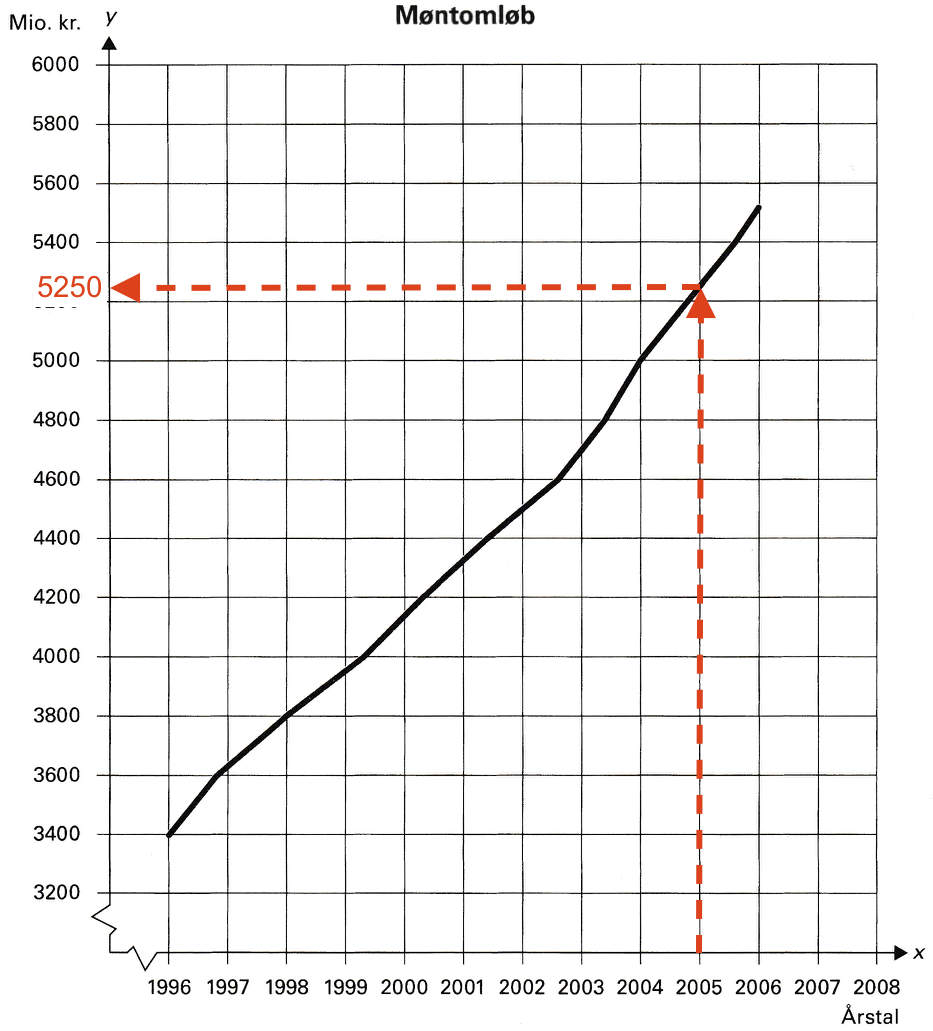
2. Linjen er tegnet ind med rødt på grafen nedenunder. Man opretter to støttepunkter ved at udregne y for x = 1996 og x = 2006.

   For x = 1996 får man y = 210·(1996 - 1996) + 3400 = 3400 og for x = 2006 får man y = 210·(2006 - 1996) + 3400 = 5500. Disse punkter er vist med cirkler nedenfor.

   

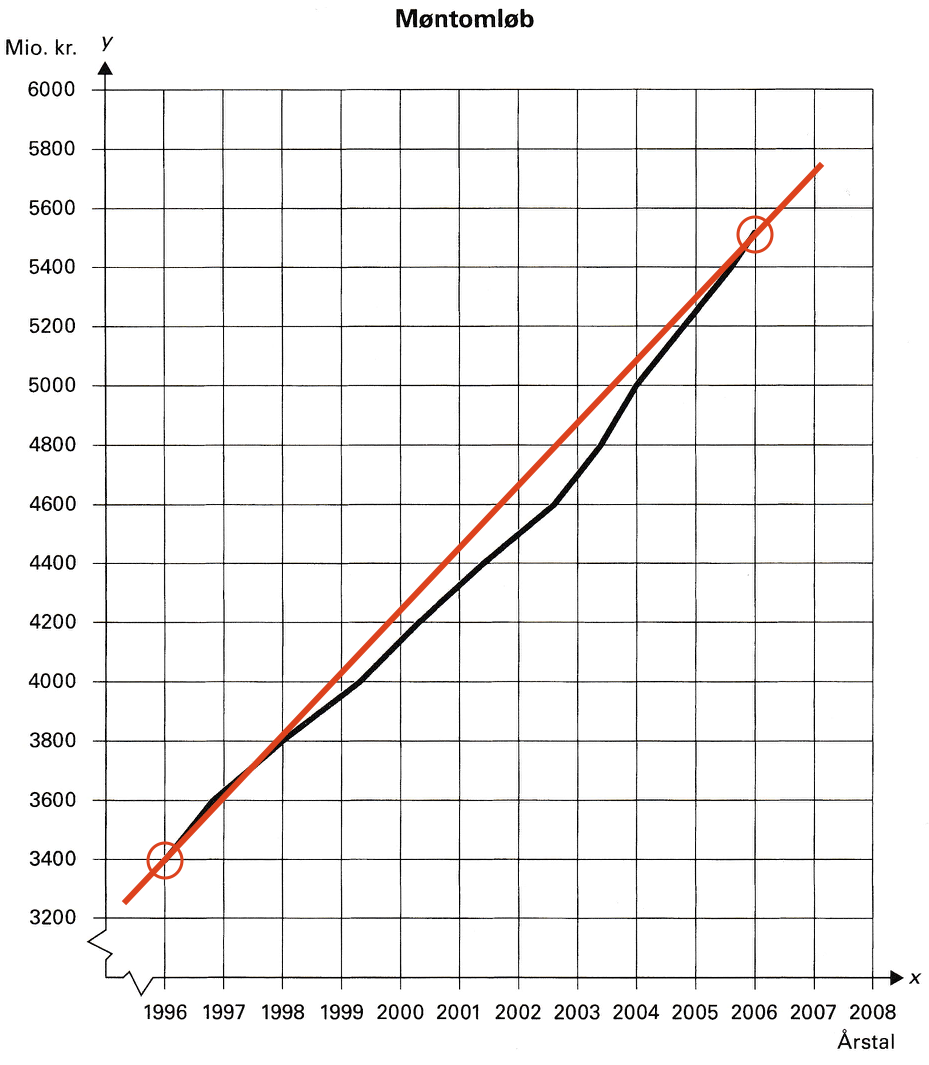
3. For 1997 giver formlen: 3400·1,05^1997-1996 = 3400·1,05 = 3570.

   For 2005 giver den: 3400·1,05^2005-1996 = 3400·1,05⁹ = 5275.

   Tallene er indsat i nedenstående tabel.

   

4. Kurven er tegnet ind ved hjælp af fire støttepunkter.

   

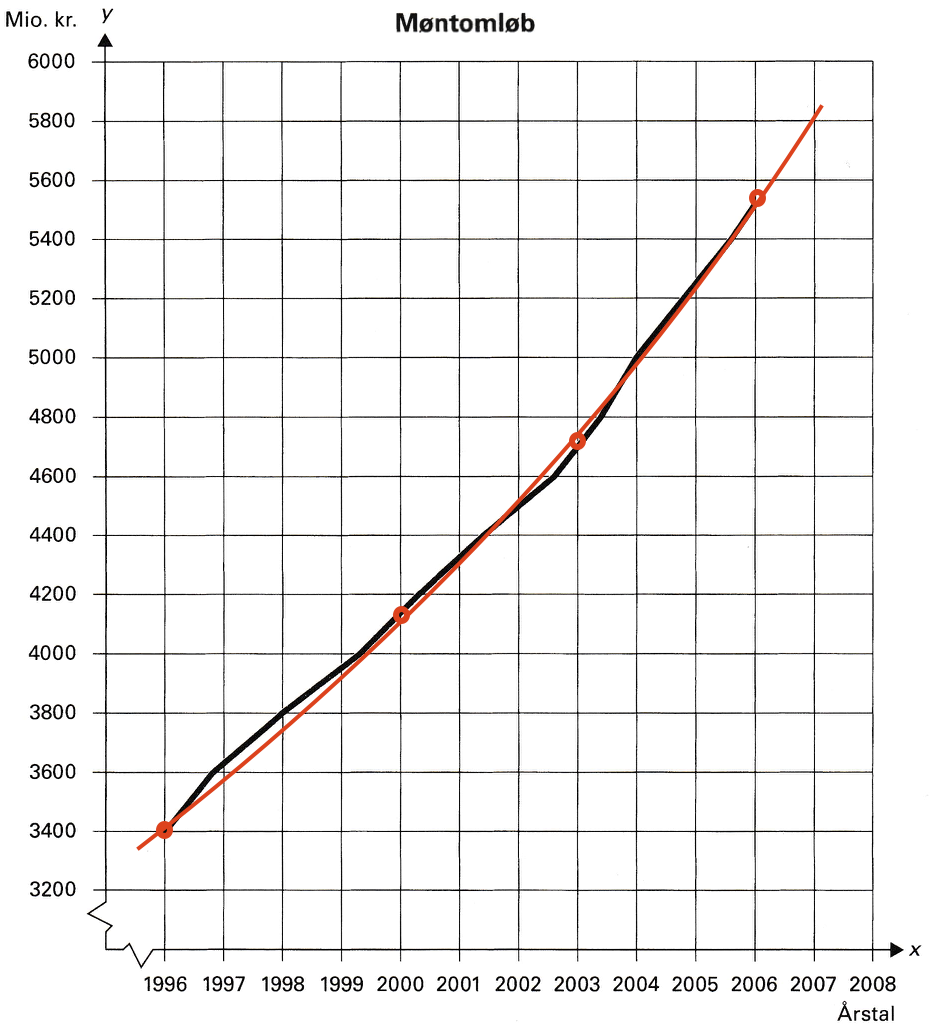
5. Model 2 passer bedst, da den ligger tættest på den sorte kurve.

Svar på opgave 4: Guld

1. Vægten af en guldbarre er (19,3 g/cm³)·(647,7 cm³) =

   19,3·647,7 g = 19,3·647,7·0,001 kg = 12,5 kg

2. Man har formlerne:

   Pris i DKK = pris i EURO gange 7,46 DKK/EURO.

   Pris i EURO = vægt af guld i ounce gange 556,5 EURO/ounce

   Vægt af guld i ounce = vægt i g divideret med 31,1.

   Det giver tilsammen følgende pris i DKK =

   ((vægt i g divideret med 31,1 g/ounce) gange 556,5 EURO/ounce) gange 7,46 DKK/EURO =

   (12500/31,1 ounce)·(556,5 EURO/ounce)·(7,46 DKK/EURO) = 1.668.605 DKK =

   1,67 mio. kr.

3. 67 tons guldbarrer svarer til følgende antal guldbarrer: 67.000 kg/(12,5 kg/barre) = 5360 guldbarrer

4. Finhed er andelen af guld i 1000.-dele. Karat er andelen af guld i 24.-dele. Antal karat kaldes x.

   Man skal omregne 585/1000 til x/24. Man får:

   585/1000 = x/24 ⇒ (585/1000)·24 = x ⇒ x = 14,04.

   Dvs. guldringen er 14 karat guld

5. Finheden er det tal, som står i tælleren, når man opgiver guldindholdet i 1000.-dele.

   Karat er det, som står i tælleren, når man opgiver guldindholdet i 24.-dele.

   Det er to måder at sige det samme på bare med forskellig nævner. Indsættes y = finhed og x = karat får man:

   y/1000 = x/24 ⇒ y = (1000/24)·x ⇒ y = 41,7·x

   Dvs. forskriften for sammenhæng mellem gulds finhed (y) og karat (x) er y = 41,7·x

Svar på opgave 5: Forhallen

1. Punkterne indtegnet:

   

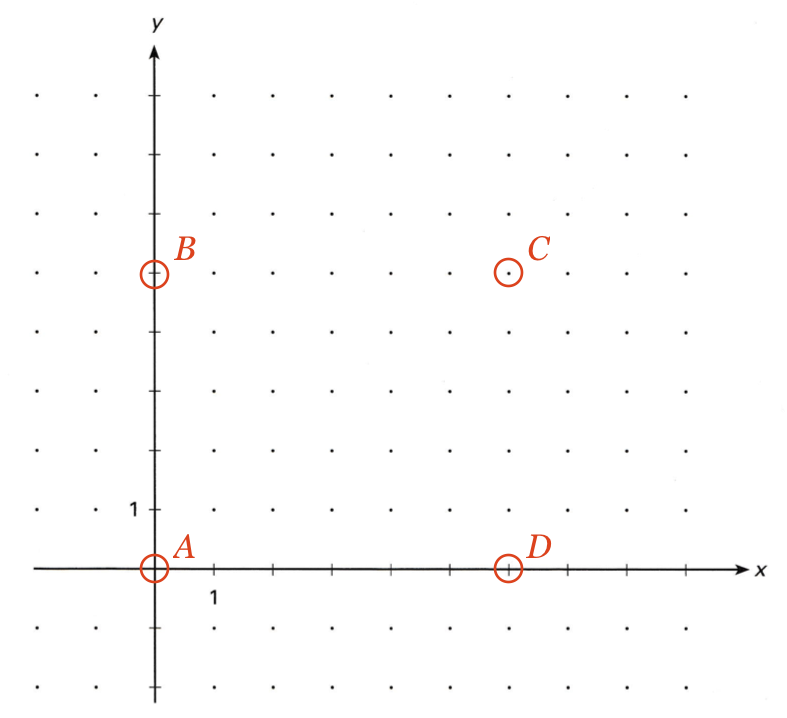
2. Linjen indtegnet. Den falder med 5 hver gang man går 4 hen ad x-aksen.

   

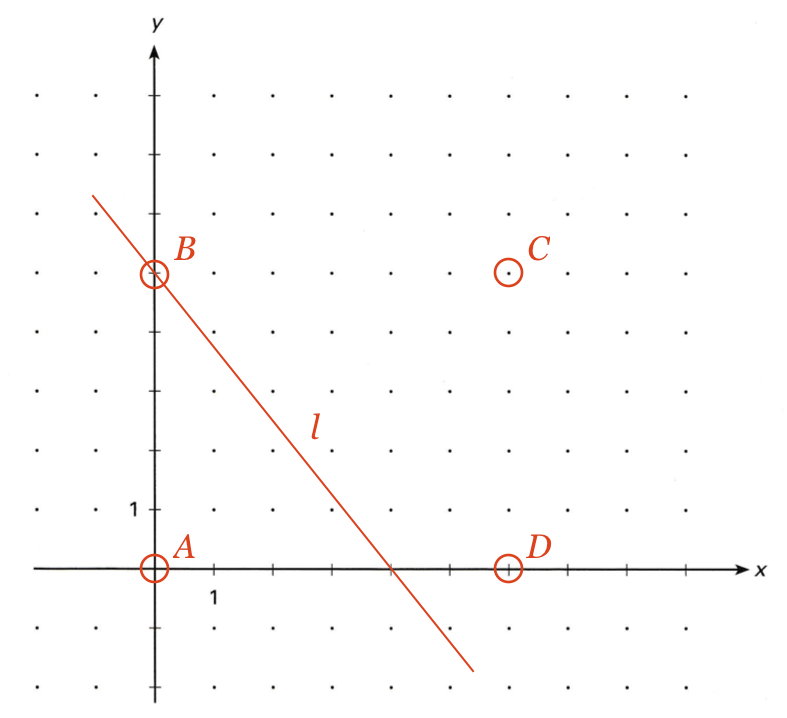
3. Retvinklet

4. Koordinatsystemet danner sammen med linjen m en retvinklet trelant, hvor man skal finde hypotenusen. Man skal finde skæringspunktet mellem m og x-aksen. Alle punkter på x-aksen har y-værdien 0. Dette indsættes i linjens ligning:

   0 = 5 - 1,25x ⇒

   1,25x = 5 ⇒

   x = 5/1,25 = 4

   Dvs. den lodrette katete har længden 5 og den vandrette katete har længden 4. Længden af hypotenusen kaldes x og findes ved hjælp af Pythagoras læresætning:

   x² = 5² + 4² ⇒

   x² = 25 + 16 ⇒

   x² = 41 ⇒

   x = √41 = 6,403

   Længden af siden er 6,4

5. Linjen m tegnet med rødt nedenunder (l er tegnet med sort).

   

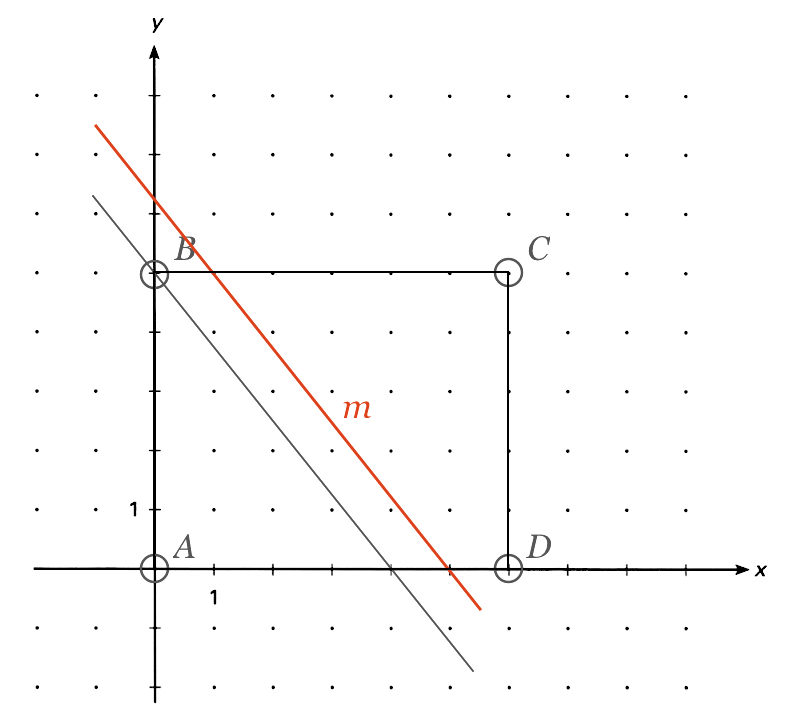
6. Linjen m skærer x-aksen for x = 5 og dermed y-aksen for y = 6,25. Den har samme hældning som l, da de to linjer er parallelle. Dvs m har ligningen y = 6,25 - 1,25x.