Svar på opgave 1: Jasmins skolevej
-
Man måler rutens længde i Geogebra som vist nedenunder. Oprindeligt skulle det måles med lineal.
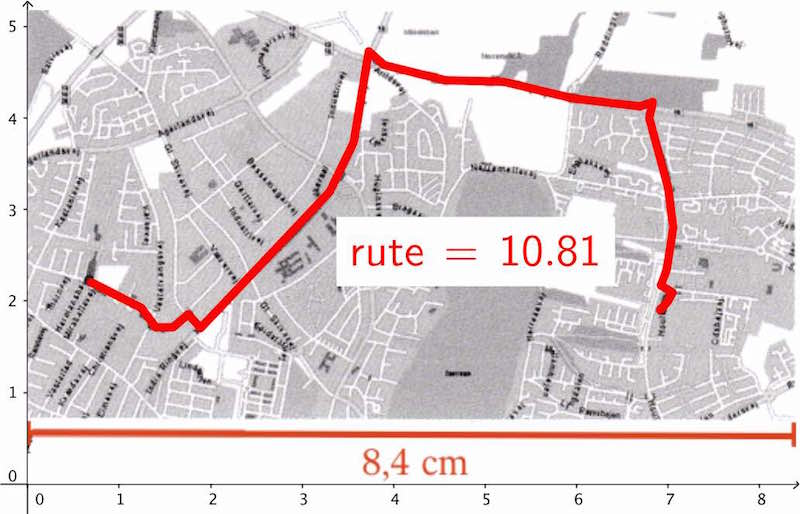
-
Man skal finde forholdet mellem længden i virkeligheden og længden på kortet. Dette er:
(6,3 km)/(10,8 cm) =
(6,3·(1000 m))/(10,8 cm) =
(6,3·1000·(100 cm))/(10,8 cm) =
630.000/10,8 = 58333,3
Dvs. målestoksforholdet er 58333:1 ≈ 60.000:1 -
Jasmins starttidspunkt er 8:15 - 25 min. =
8 timer og 15 min. - 25 min. =
8 timer + 15 min - 25 min. =
8 timer - 10 min. =
(7 timer + 60 min.) - 10 min. =
7 timer + 50 min. = 7 timer og 50 min. = 7:50.
Dvs. Jasmin skal køre hjemmefra kl. 7:50 for at møde til tiden. -
Jasmin skal køre 6,3 km på 20 min. Hastighed = strækning divideret med tid. Det skal udregnes i km/t, der her giver:
(6,3 km)/(20 min.) =
(6,3 km)/(20·(1/60 t)) =
6,3/(20/60) km/t=
6,3·(60/20) km/t=
6,3·3 km/t =
18,9 km/t
Dvs. Jasmins gennemsnitshastighed skal være 18,9 km/t
Svar på opgave 2: Elev i 10. klasse
-
Den procentvise nedgang er [(start - slut)/start]·100 % =
[(40722 - 34428)/40722]·100 % = 15,5 % -
Man skal bruge fremskrivningsformlen: K = K0·(1 + r)n, hvor K er antallet af elever, der vælger 10. klasse i 2010, K0 er antallet af elever, der vælger 10. klasse i 2005, r er vækstraten og n er antallet af år.
Man skal finde K, når K0 = 34.428, r = -2 % og n = 2010 - 2005 = 5. Dette giver:
K = 34.428·(1 - 2 %)5 ⇔
K = 34.428·(0,98)5 ⇔
K = 34.428·0,9039 ⇔
K = 31.120
Dvs. antallet af 10.-klasse elever i 2010 forventes at blive 31.120 -
Man antager, at antallet af 10.-klasse elever på efterskoler vokser med en fast årlig vækstrate. Man bruger samme formel som i forrige spørgsmål, men man skal nu finde r.
Perioden er på 2005 - 1996 = 9 år. K0 = 12407 og K = 15044. Dette giver følgende ligning med hensyn til r:
15044 = 12407·(1 + r)9 ⇔
15044/12407 = (1 + r)9 ⇔
9√[15044/12407] = (1 + r) ⇔
9√[15044/12407] - 1 = r ⇔
r = 0,0216 = 0,0216·100 % = 2,16 %
Dvs. den gennemsnitlige årlige vækstrate er 2,16 %
Svar på opgave 3: Undersøgelser i 10. klasse
- Antallet af elever i Jasmins klasse er 4 + 12 + 7 + 3 + 2 = 28
-
Nedenunder er fordelingen af elever med et bestemt antal søskende vist på et søjlediagram, som er lavet i Excel.
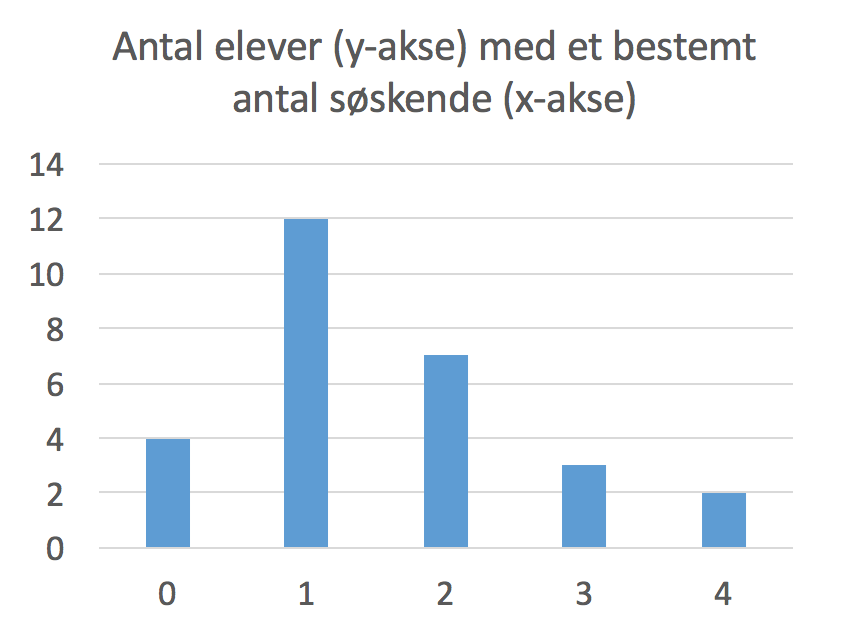
-
Nedenunder er søjlerne med de elever, der tjener over 1500 kr. farvet røde.
Der er sammenlagt 4 + 9 = 13 elever, der tjener over 1500 kr. I alt er der 8 + 6 + 1 + 4 + 9 = 28 elever.
Dvs. andelen af elever, der tjener over 1500 kr. er (13/28)·100 % = 46,4 %
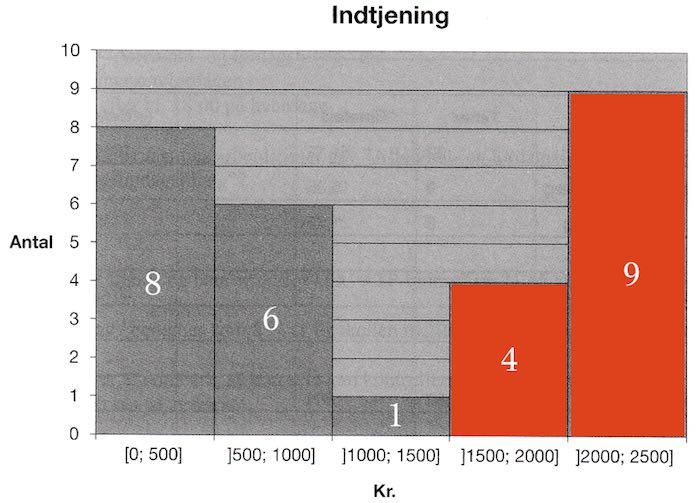
-
Middeltallet beregnes ved at gange midten af hvert interval med frekvensen af intervallet. Frekvensen er hyppigheden eller antallet af elever i intervallet divideret med antallet af elever i alt.
Man får middeltallet af elevernes indtægt til: [250·(8/28) + 750·(6/28) + 1250·(1/28) + 1750·(4/28) + 2250·(9/28)] kr. = 1250 kr.
(Middeltal og gennemsnit er det samme, blot bruges middeltal om grupperede data (data inddelt i intervaller), mens gennemsnit bruges om ugrupperede data).
Svar på opgave 4: Sommerferiejobbet
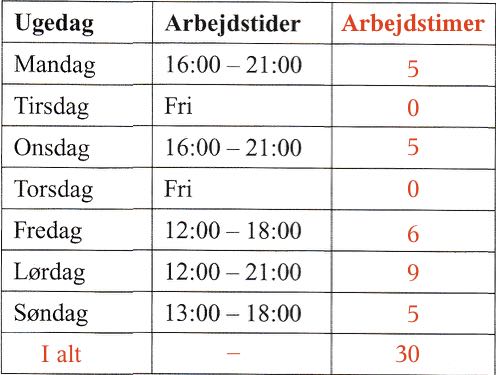
- Antallet af normaltimer uden tillæg, som Jasmin arbejder, er (32 - 9 - 6) timer = 17 timer
-
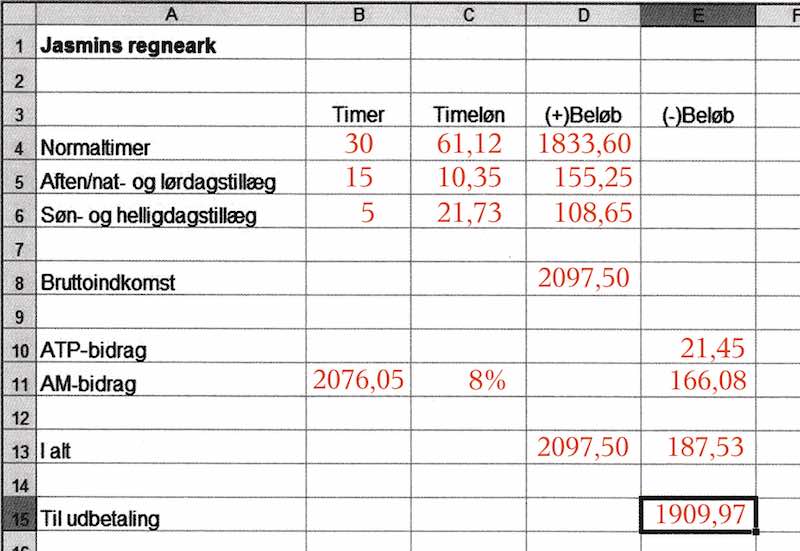
Lønsedlen er vist nedenunder. Summerne af (+) beløb og (-) beløb er markeret med røde ringe.
I uge 27 får Jasmin i alt udbetalt (+) beløb minus (-) beløb = 2179,37 kr. - 194,08 kr. = 1985,29 kr.
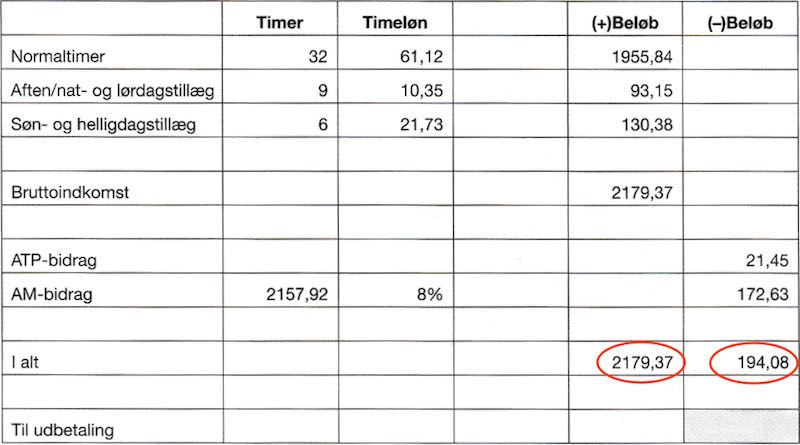
-
Jasmins arbejdstimer beregnes ud fra skemaet over hendes arbejdstider. Dette er vist nedenunder.
Hun arbejder i alt 30 timer i uge 28.
-
Jasmin havde (6 + 9) timer = 15 timer med aften-, nat- og lørdagstillæg i uge 28.
Jasmin havde 5 timer med søn- og helligdagstillæg i uge 28. -
Nedenfor er vist det udfyldte regneark. Timeløn-satserne er hentet fra opgavens lønseddel, og regnearket er i øvrigt lavet efter den.
I uge 28 får Jasmin udbetalt 1.909,97 kr.
Svar på opgave 5: Eleverne spiller Meyer
-
Nedenfor er vist en tabel over de forskellige slag, som antal øjene på den ene terning komma antal øjne på den anden. Antal øjne på den ene trekant er vist henad og antal øjne på den anden er vist nedad. Der er i alt 36 udfald. De to udfald, der giver "meyer" er vist med rødt.
Da der er to gunstige udfald ud af 36 mulige, er sandsynligheden 2/36 = 0,056 = 5,6 %
1 2 3 4 5 6 1 1,1 1,2 1,3 1,4 1,5 1,6 2 2,1 2,2 2,3 2,4 2,5 2,6 3 3,1 3,2 3,3 3,4 3,5 3,6 4 4,1 4,2 4,3 4,4 4,5 4,6 5 5,1 5,2 5,3 5,4 5,5 5,6 6 6,1 6,2 6,3 6,4 6,5 6,6 -
Nedenfor er igen vist en tabel over de forskellige slag. De udfald, der giver hændelsen eller slaget "53" er blå og det udfald, der giver hændelsen "par 6", er rødt.
Da hændelsen "53" har to gunstige udfald ud af 36 mulige, er sandsynligheden 2/36 = 5,6 %
Da hændelsen "par 6" har eet gunstigt udfald ud af 36 mulige, er sandsynligheden 1/36 = 2,8 %. Dermed er sandsynligheden mindre for "par 6" end for "53".
1 2 3 4 5 6 1 1,1 1,2 1,3 1,4 1,5 1,6 2 2,1 2,2 2,3 2,4 2,5 2,6 3 3,1 3,2 3,3 3,4 3,5 3,6 4 4,1 4,2 4,3 4,4 4,5 4,6 5 5,1 5,2 5,3 5,4 5,5 5,6 6 6,1 6,2 6,3 6,4 6,5 6,6 -
Tabellen herunder viser med rød skrift de udfald, der er bedre end "65".
Det ses, at 10 udfald er bedre end 65, og dermed er sandsynligheden for at slå bedre end 65 lig med 10/36 = 0,278 = 27,8 %
1 2 3 4 5 6 1 1,1 1,2 1,3 1,4 1,5 1,6 2 2,1 2,2 2,3 2,4 2,5 2,6 3 3,1 3,2 3,3 3,4 3,5 3,6 4 4,1 4,2 4,3 4,4 4,5 4,6 5 5,1 5,2 5,3 5,4 5,5 5,6 6 6,1 6,2 6,3 6,4 6,5 6,6 -
Tabellen herunder viser med rød skrift en repræsentant for hver af de forskellige hændelser eller slag i meyer.
Der ses at være 21 forskellige slag eller rettere kombinationer af øjne.
1 2 3 4 5 6 1 1,1 1,2 1,3 1,4 1,5 1,6 2 2,1 2,2 2,3 2,4 2,5 2,6 3 3,1 3,2 3,3 3,4 3,5 3,6 4 4,1 4,2 4,3 4,4 4,5 4,6 5 5,1 5,2 5,3 5,4 5,5 5,6 6 6,1 6,2 6,3 6,4 6,5 6,6
Svar på opgave 6: Mobiltelefonen
-
Jasmins udgifter i en måned med 200 SMS'er er: 200·(0,21 kr.) = 42 kr.
Caspers udgifter i en måned med 200 SMS'er er: 49 kr. + 200·(0,01 kr.) = 49 kr. + 2 kr. = 51 kr.
Forskellen er 51 kr. - 42 kr. = 9 kr. -
Nedenfor er tabellen udfyldt.

-
Nedenfor er graferne for de to abonnementer afbildet.
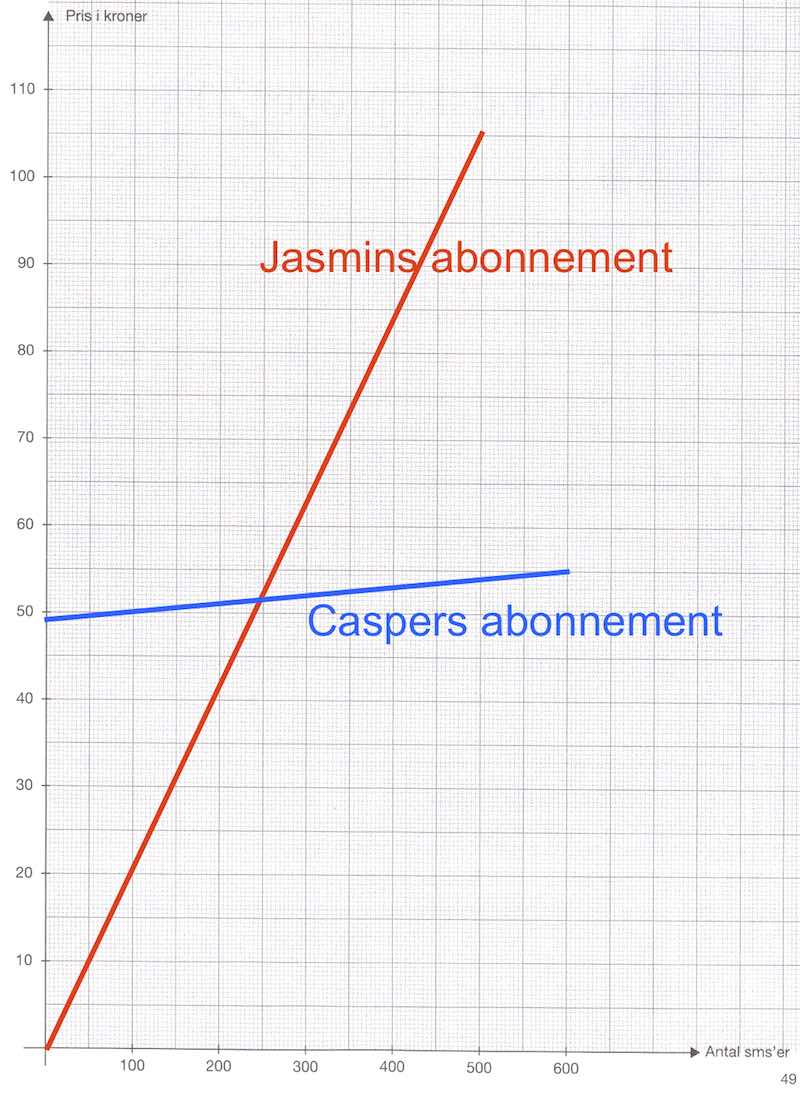
- Funktionsforskriften for Caspers abonnement er y = 49 + x·0,01, hvor x er antallet af SMS'er på en måned og y er abonnementsudgiften for en måned.
-
x-koordinaten til skæringspunktet findes ved af sætte de to funktionsforskrifter lig med hinanden og løse den fremkomne ligning med hensyn til x. Man får:
0,21·x = 49 + 0,01·x ⇔
0,21·x - 0,01·x = 49 ⇔
0,2·x = 49 ⇔
x = 49/0,2 ⇔
x = 245
For at finde skæringspuktets y-værdi indsætter man den fundne x-værdi i den ene forskrift for y (begge forskrifter giver samme y-værdi). Man får: y = 0,21·245 = 51,45
Dvs. skæringspunktet er (x,y) = (245;51,45) -
Det fundne x = 245 er det antal SMS'er, hvor deres abonnementer er lige dyre på en måned.
y = 51,45 er det som abonnementet koster for begge i en måned, hvor de sender 245 SMS'er. -
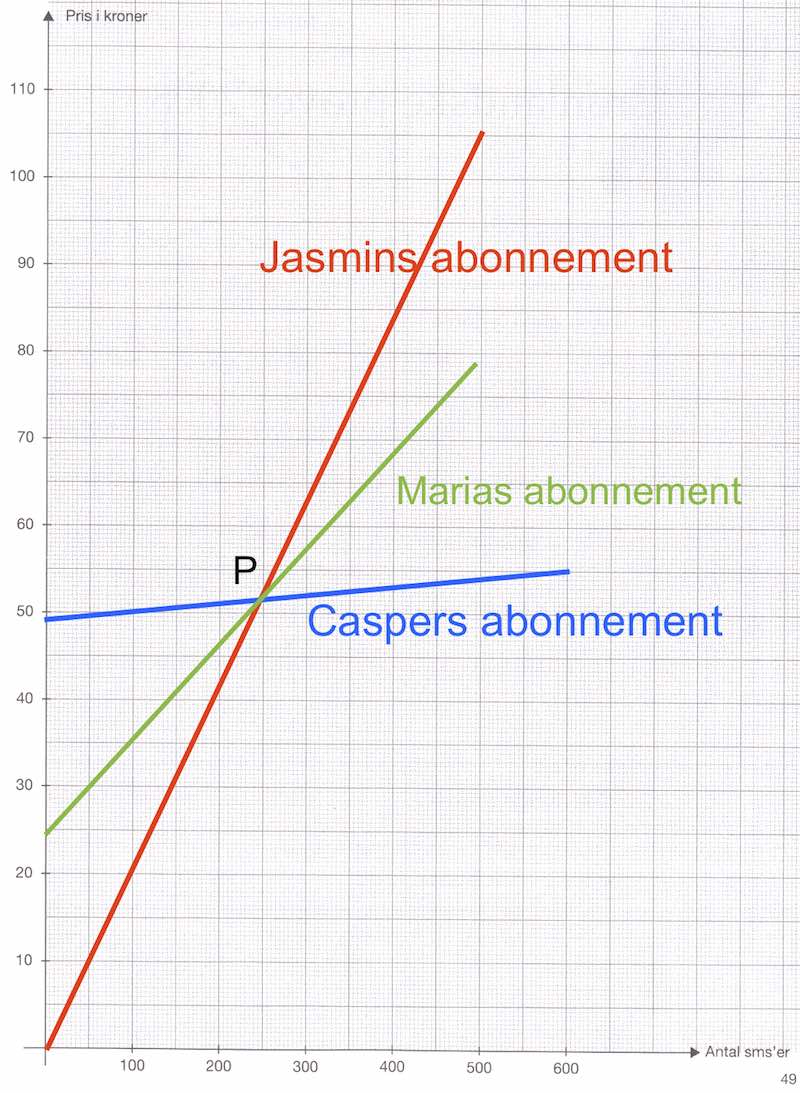
Nedenfor er graferne for de tre abonnementer inklusive Marias afbildet.
-
Marias abonnement koster 24,50 kr. plus (antal SMS'er gange prisen på een SMS).
Da grafen for hendes abonnement går gennem punktet P = (245;51,45) betyder det, at en måned, hvor hun sender 245 SMS'er er hendes abonnement 51,45 kr.
Kaldes prisen på en SMS for a, får man ligningen: 51,45 kr. = 24,50 kr. + 245·a ⇔
51,45 kr. - 24,50 kr. = 245·a ⇔
26,95 kr. = 245·a ⇔
26,95 kr./245 = a ⇔
a = 0,11 kr.
Dvs. prisen for en SMS med Marias abonnement er 11 øre
(Grunden til at den ubekendte kaldes a og ikke x, er at x før blev brugt om antallet af SMS'er, hvor vi her leder efter prisen på een SMS.)
Svar på opgave 7: Jasmins værelse
-
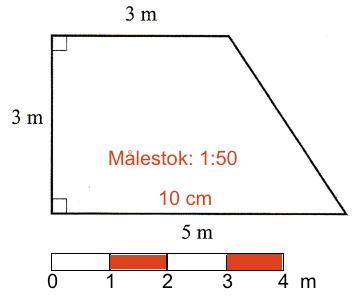
på tegningen nedenunder skal nederste side på trapezen forestille at være 10 cm. Tegningen har målestoksforhodlet 1:50.
-
Arealet af trapezen er 3·(3 + 5)/2 m2 = 12 m2.
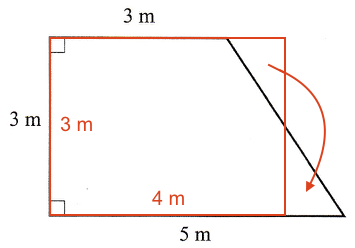
Antallet af meter, som hun skal købe, afhænger af om hun vil have gulvtæppet i eet stykke, eller om hun vil være tilfreds med, at det deles op i to. (Normalt foretrækkes eet stykke).
Hvis hun deler tæppet i to, så skal hun købe (3 m)·(4 m) = 12 m2
Dette er vist på tegningen nedenunder.
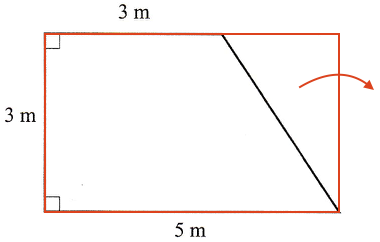
Hvis hun vil have gulvtæppet i et stykke, så skal hun købe 3·5 m2 = 15 m2
Dette er vist nedenunder. Her går det trekantede stykke til spilde.
-
Hun køber 15 m2 og bruger 12 m2. Dette giver følgende procentdel for, hvor stor en del af tæppet, som bruges:
(12/15)·100 % = 80 % -
Værelset er en trapez, der kan deles op i et kvadrat og en retvinklet trekant som vist herunder.
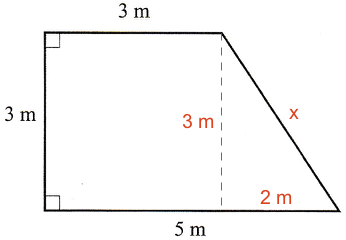
Man skal finde hypotenusen x, og det gøres ved hjælp af Pythagoras læresætning:
x2 = 22 + 32 ⇔
x2 = 13 ⇔
x = √13 ≈ 3,61
Dvs. listens længde er 2·(3 m) + 5 m + 3,61 m = 14,6 m