Svar på opgave 1: Uddannelse til animator

1. Det samlede antal point er: (3,5 år)·(60 point/år) = 210 point

2. Antallet point om året er 60 point. Antal timer pr. point er defor: (1680 timer)/(60 point) = (1680/60) timer/point = 28 timer pr. point

3. Hun bruger 28 timer på hver af de 14 point. Hendes tidsforbrug er i alt: (14 point)·(28 timer/point) = 392 timer

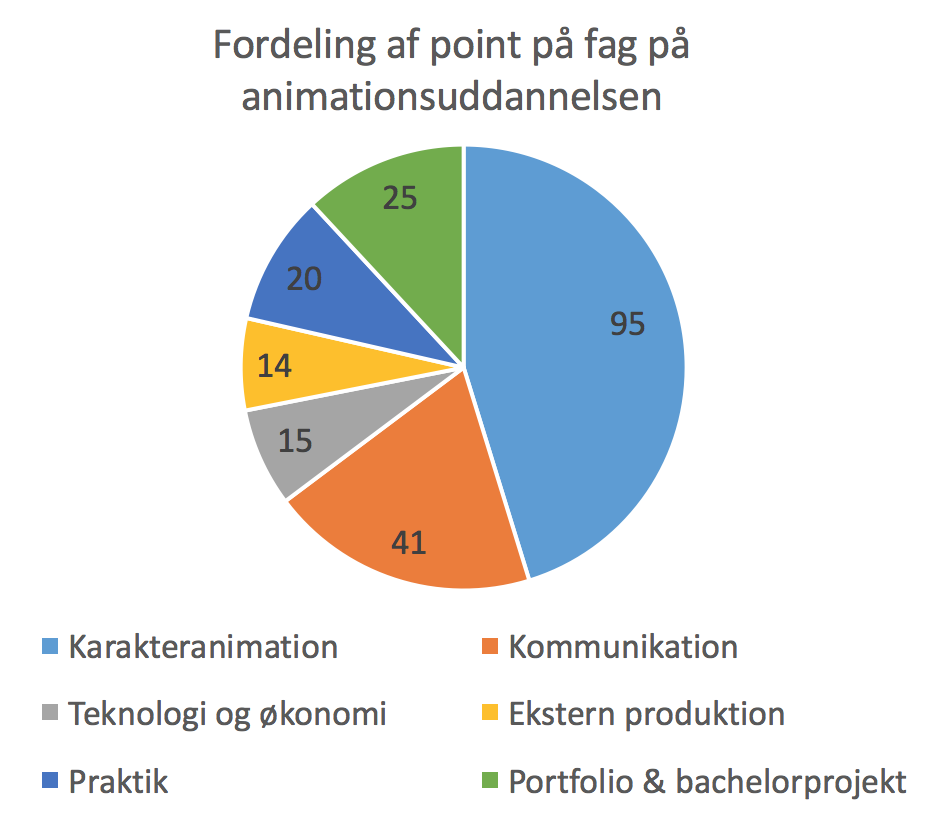
4. Nedenfor er vist et cirkeldiagram over pointfordelingen for uddannelsen. Dette diagram er lavet i Excel.

   

5. Der går i gennemsnit 4,3 uger på en måned, men for nemheds skyld regnes med 4 uger. Fire måneder er derfor lig med 4·4 uger = 16 uger.

   Hun holder ferie undervejs i 2 uger og studerer derfor i 14 uger.

   Den del af kommunikationskurset, der ligger på andet semester giver 19 point og tager derfor 19·28 timer = 532 timer.

   Disse timer skal fordeles på 14 uger, dette giver 532/14 timer/uge = 38 timer/uge

Svar på opgave 2: Rundt om animation

1. Der er gået følgende antal år siden praksinoskopet blev opfundet: (2006 - 1877) år = 129 år

2. Omkreden af cylinderen er 9,14 m. I en cirkel er omkreds lig med diameter gange π eller diameter = omkreds/π.

   Dette giver følgende diameter: 9,14 m/π = 2,91 m

3. Omsætninger er steget med: (1 mia. kr.) - (20 mio. kr.) = (1.000.000.000 - 20.000.000) kr. = 980.000.000 kr. = 980 mio. kr.

4. Start = 20 mio, slut = 1 mia. Man får følgende stigning i procent:

   [(1 mia. - 20 mio.)/(20 mio.)]·100 % = (980.000.000/20.000.000)·100 % = (98/2)·100 % = 4900 %

5. Den årlige vækstprocent eller vækstrate beregnes ved hjælp af fremskrivningsformlen eller opsparingsformlen. Denne formel er:

   K = K₀·(1 + r)ⁿ, hvor man skal finde vækstraten r, idet K = 1 mia. kr., K₀ = 20 mio. kr. og n = (2005 - 1988) = 17. Man får:

   1.000.000.000 = 20.000.000·(1 + r)¹⁷ ⇔

   1.000.000.000/20.000.000 = (1 + r)¹⁷ ⇔

   50 = (1 + r)¹⁷ ⇔

   ¹⁷√50 = (1 + r) ⇔

   1,25875 = 1 + r ⇔

   r = 1,25875 - 1 ⇔

   r = 0,25875

   Dvs. den årlige vækstprocent har været 0,25875 = 25,9 %

Svar på opgave 3: Bolden hopper

1. Nedenfor er de manglende t- og x-værdier indsat i tabellen.

   

2. Nedenfor er de manglende y-værdier indsat i tabellen. Beregningerne er 6·0,45 - 5·0,45² = 1,6875 og 6·0,75 - 5·0,75² = 1,6875.

   

3. Nedenfor er grafen for boldens første hop tegnet:

   

   Forskriften er y = x - 5·(x/6)², idet t = x/6. x ligger mellem 0 og 7,2 meter, da t ligger mellem 0 og 1,2 s, og da x = 6·t, hvor x regnes i meter og t i sekunder.

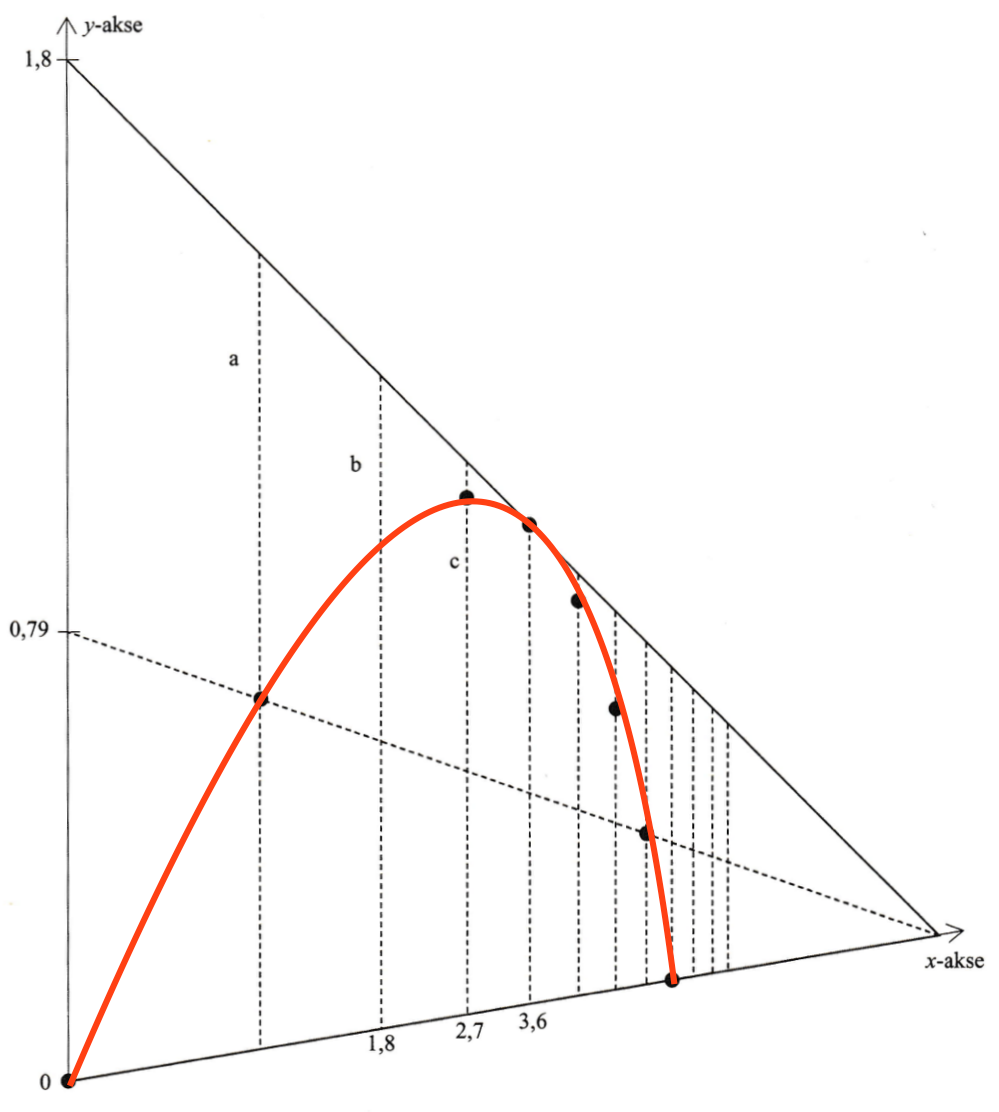
4. Firkanten ABCD på perspektivtegningen nedenfor er i virkeligheden et rektangel. Rektanglets diagonaler er vist med punkterede linjer.

   

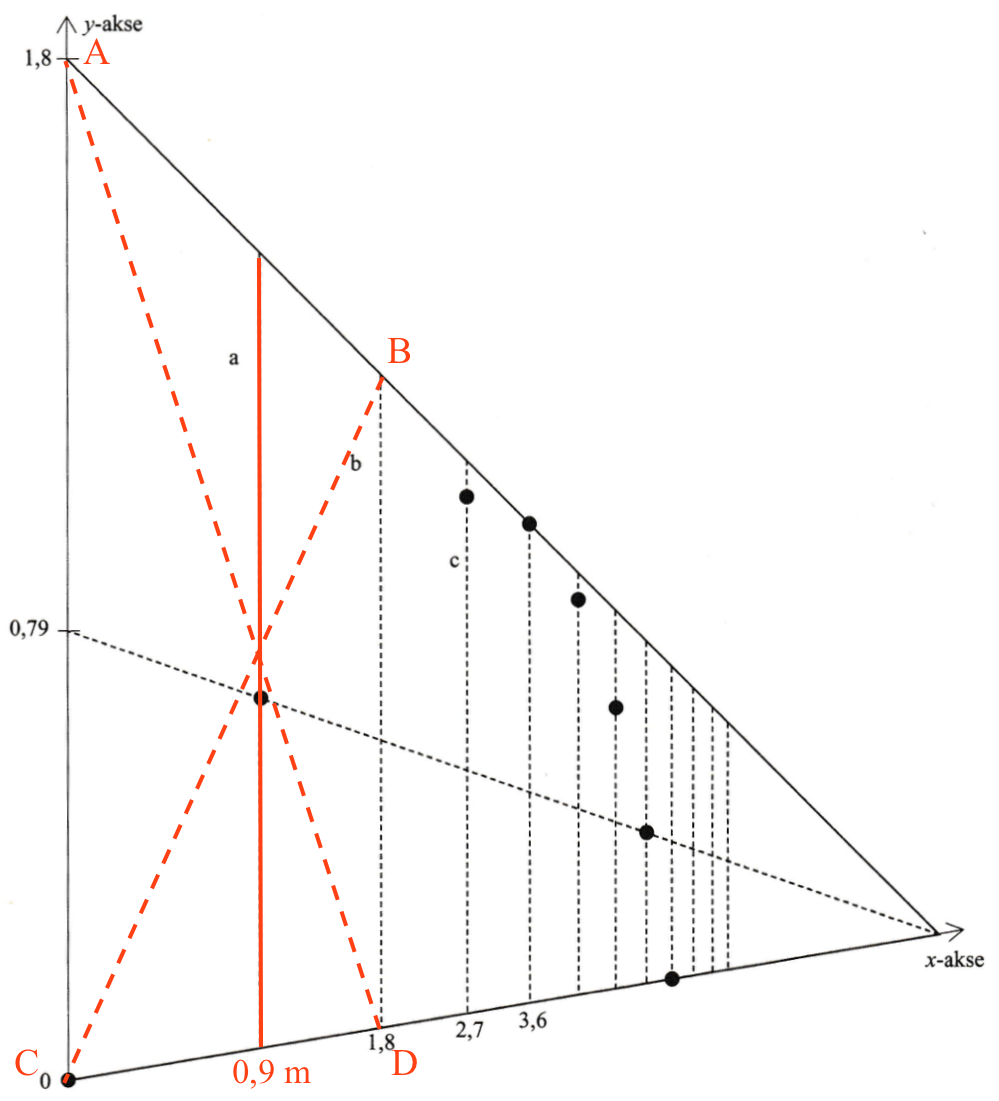
   Linjestykket a går lodret gennem skæringspunktet for diagonalerne og halverer linjestykket CD. Dermed er der 0,9 m fra linjestykke a til linjestykke b, der er lig med rektanglets lodrette side BD.

   Dermed er der samme længde, nemlig 0,9 m mellem linjestykke a og linjestykke b henholdsvis linjestykke b og linjestykke c.

5. Nedenfor er parablen tegnet i perspektiv.

   

6. Startstedet findes for t = 1,2 s, mens slutstedet findes for t = 2,1 s.

   Startsted = (4,5·1,2 + 1,8) m = 7,2 m

   slutsted = (4,5·2,1 + 1,8) m = 11,25 m

   Længden af hoppet er slutsted - startsted = (11,25 - 7,2) m = 4,05 m

7. Det højeste y-værdi indtræffer for det t, der ligger midt mellem t = 1,2 s og t = 2,1 s, dvs. for t = 1,65 s.

   Dvs. den højeste højde er: (-5·(1,65)² + 16,5·1,65 - 12,6) m = 1,0125 m = 1,0 m

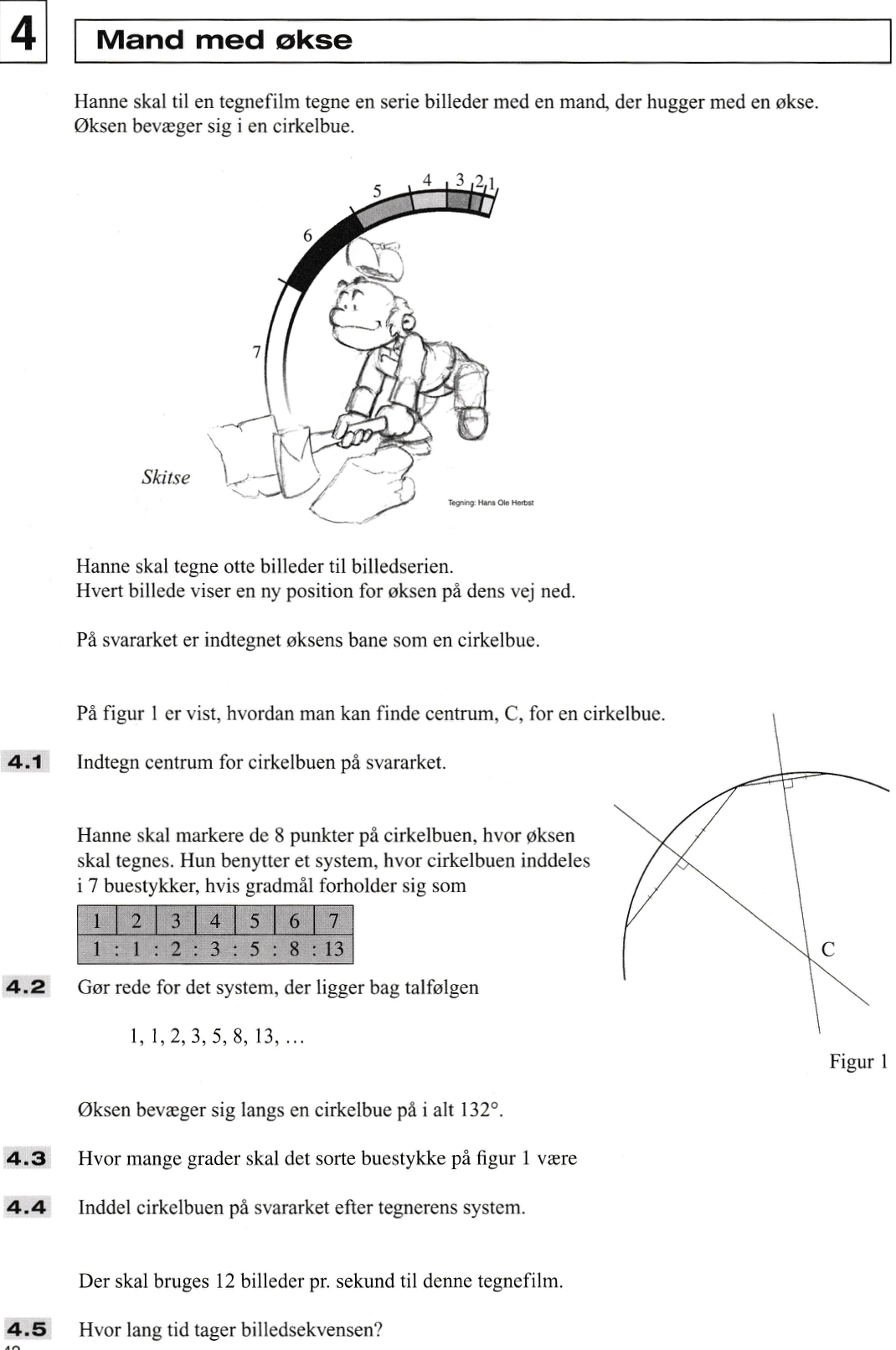
Svar på opgave 4: Mand med økse

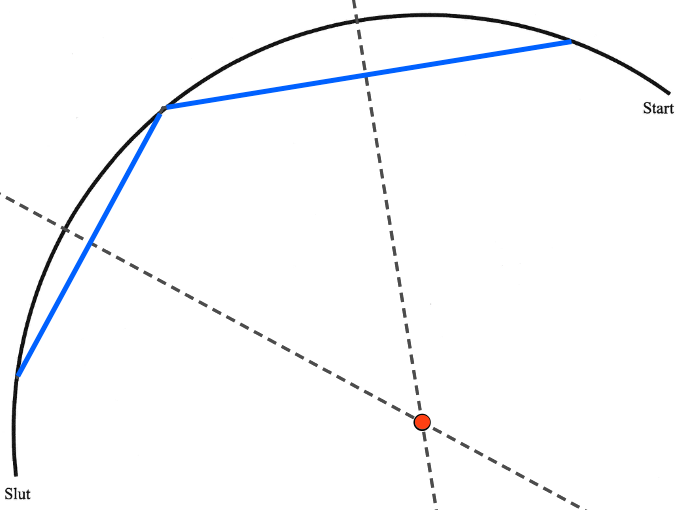
1. Nedenunder er centrum konstrueret i Geogebra og vist med rødt. Midtnormalerne til de to blå korder er vist som stiplede linjer.

   

2. Fibonacci-følgen: Man starter med to 1-taller. Disse lægges sammen, og man får 2. De øvrige fås ved at lægge de to sidste tal sammen i følgen. (1 og 2 lægges sammen til 3...2 og 3 lægges sammen til 5...osv.)

3. Vinklen på det sorte stykke kaldes x. X forholder sig til 132°, som 8 forholdet sig til summen af tallene i tabellen: 1 + 1 + 2 + 3 + 5 + 8 + 13 = 33. Man får følgende ligning for x:

   x/(132°) = 8/33 ⇔

   x = (132°)·8/33 ⇔

   x = 32°

   Dvs. den sorte vinkel er 32°

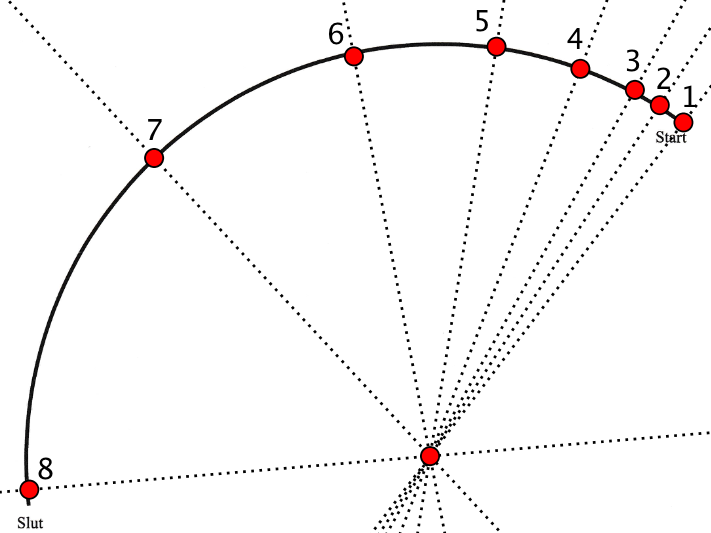
4. Nedenunder er inddelingen lavet i Geogebra.

   

5. Der er 8 billeder. Disse tager følgende antal sekunder for at blive vist: (8 billeder)/(12 billeder/sekund) = 8/12 sek. = 0,67 sek.

Svar på opgave 5: Produktion af tegnefilm

1. Tegneren skulle fremstille følgende antal billeder: (20 sek.)·(12 billeder/sek.) = 240 billeder

2. En 20 sekunders film havde følgende længde i meter: (30 fod)·(0,3048 meter/fod) = 30·0,3048 meter = 9,14 meter

   Til 1 minut skal der bruges 60 sek./20 sek. = 3 stk. af disse film. Dvs. længden af 1 min. film bliver: 3·9,14 m = 27,4 m

3. Tegneren skal fremstille følgende antal billeder på et år: (7 billeder/dag)·(5 dage/uge)·(45 uger/år) = 7·5·45 billeder/år = 1575 billeder/år

4. En tegner fremstiller følgende antal sekunds film på en år: (1575 billeder/år)/(12 billeder/sek.) = (1575/12) sekunders film/år = 131,25 sekunder film på et år

5. Een tegner kan færddiggøre 2·131,25 sekunder film på to år = 262,50 sekunders film.

   1 time og 33 min. svarer til følgende antal sekunder: 1 time og 33 min. =

   1 time + 33 min. =

   1·(3600 sek) + 33·(60 sek.) =

   5580 sek.

   Dette kræver følgende antal tegnere på to år: (5580 sek. film)/(262,50 sek. film/tegner) =

   (5580/262,50) tegnere = 21,3 tegnere.

   Dette skal rundes op, så der i alt skal ansættes 22 tegnere