Klik på hver enkelt opgave for at se løsning.
Opgave 1. Terrasse med fliser. (Forholdstal og regning med enheder).
En terrasse har form som et rektangel. Den er 5 m lang og 3 m bred.

En terrasse har form som et rektangel. Den er 5 m lang og 3 m bred.

- Hvad er terrassens areal? Terrassen indeholder et 5 cm tykt lag af grus.
- Hvad er grusets rumfang? En sæk med grus indeholder 0,2 m3
- Hvor mange sække med grus skal mindst købes til terrassen? Man lægger fliser oven på gruset. Hver flise er 50 cm på hver led. Hver anden række af fliser indeholder udelukkende hele fliser, mens hver anden række starter og slutter med en halv flise. Nogle af fliserne er vist nedenunder.
- Hvor mange hele og halve fliser er der på terrassen? Terrassen hælder på tværs, så den er 1,5 cm højere i den ene side end den anden.
- Hvor mange procent hælder terrassen?

Svar på opgave 1:
- Terrassens areal er (3 m)·(5 m) = 15 m2
- Rumfanget af gruset er arealet af terrassen gange gruslaget tykkelse = (15 m)·(0,05 m) = 0,75 m3
-
Antallet af sække som decimaltal er (0,75 m3)/(0,2 m3/sæk) = 3,75 sække.
Man kan kun købe et helt antal sække og undersøger om man skal runde op eller ned:
3 sække indeholder: (0,2 m3)·3 = 0,60 m3, hvilket er for lidt.
4 sække indeholder: (0,2 m3)·4 = 0,80 m3 , hvilket er tilstrækkeligt.
Dvs. der skal bruges 4 sække med grus. -
Antallet af rækker af fliser er (3 m)/(0,5 m/række) = 6 rækker. Dvs, der er 3 rækker af hver slags.
Hver række med udelukkende fliser indeholder (5 m)/(0,5 m/hel flise) = 10 hele fliser.
Hver række med halve fliser indeholder 2 halve og (5 m - 2·0,5 m)/(0,5 m/hel flise) = 9 hele fliser.
Der er 3 rækker med 2 halve fliser i hver. I alt: 6 halve fliser
Der er 3 rækker med 10 hele fliser i hver og 3 rækker med 9 hele fliser i hver. I alt: 57 hele fliser -
Terrassen falder 0,015 m over en strækning på 3 m. Over en strækning på 100 m, så svarer dette til et fald på: (0,015 m)·(100 m)/(3 m) = 0,5 m.
Dette vil sige, at terrassens hældning er på 0,5 %
Opgave 2. Rombe. (Geometri I).
En rombe er en firkant med ens sider. Modstående vinkler er parvis ens. Diagonalerne halverer hinanden og skærer hinanden i en ret vinkel.
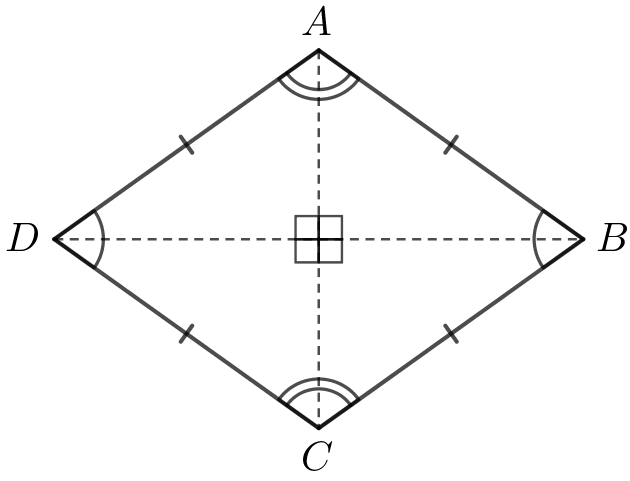
En rombe er en firkant med ens sider. Modstående vinkler er parvis ens. Diagonalerne halverer hinanden og skærer hinanden i en ret vinkel.

-
I en bestemt rombe er diagonalernes længder 4 og 7.
- Hvad er rombens areal? En roset består af 7 ens romber som vist. Vinklerne kaldes u og v.
- Hvor mange grader er u og v? En rombe har sidelængden 5 samt vinkler på 60° og 120°.
- Hvor lang er den længste diagonal?

Svar på opgave 2:
-
Rombens areal er halvdelen af produktet af diagonalernes længder. Dette er vist nedenfor, hvor romben er indskrevet i et rektangel, der er dobbelt så stor som romben, og hvor rombens diagonaler er lig med rektanglets sider.

Dvs. rombens areal er 0,5·4·7 = 14 -
Vinklen u er en syvendedel af 360°. Dvs. u = 51,4°
Angående vinklen v:
Romben indeholder to vinkler, som er lig med u og to som er lig med v. Vinklernes sum er 360°. Dvs.:
2·u + 2·v = 360° ⇒ v = (360° - 2·u)/2 ⇒ v = (360° - 2·51,4°)/2 = 128,6°.
Dvs. vinkel u = 129° -
Som vist nedenunder kan romben deles ind i fire ens retvinklede trekanter med vinklerne 30°, 60° og 90°. Den retvinklede trekant har hypotenusen 5.
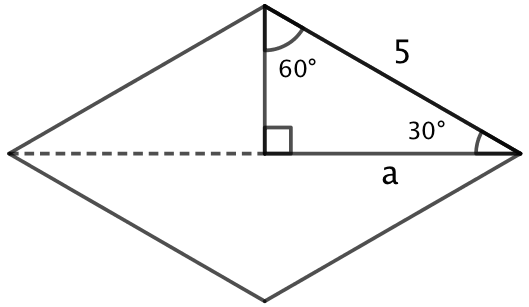
Man skal finde kateten a i den viste trekant og gange dem med 2 for at finde diagonalens længde.
For en retvinklet trekant gælder, at en katetes længde er lig med længden af hypotenusen gange sinus til den modstående vinkel.
Dette giver a = 5·sin(60°) = 4,33. Dermed er diagonalens længde: 2·4,33 = 8,66
Opgave 3. Dragefirkant. (Geometri II).
En dragefirkant består af to par af ens sider, der hver ligger op til hinanden. Det ene par af modstående vinkler er ens. Diagonalerne skærer hinanden i en ret vinkel.
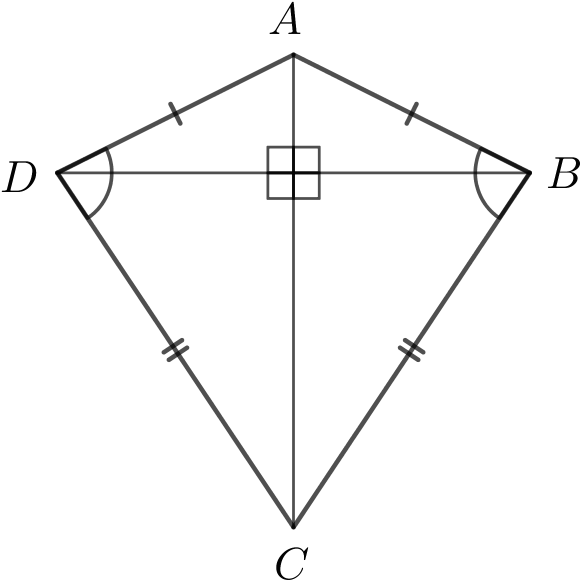
I det følgende henviser A, B, C og D til tegningen.
En dragefirkant består af to par af ens sider, der hver ligger op til hinanden. Det ene par af modstående vinkler er ens. Diagonalerne skærer hinanden i en ret vinkel.

I det følgende henviser A, B, C og D til tegningen.
-
En dragefirkant har diagonaler med længderne 12 og 16.
- Hvad er dragefirkantens areal? En vinkel i en dragefirkant er 30°, mens dens modstående vinkel er 110°.
- Hvor store er de to andre vinkler? I en bestemt dragefirkant er de to ens vinkler hver 90°. |AB| = 10 og |BC| = 18.
- Hvad er længden af dragefirkantens længste diagonal AC? (Med 1 decimal).
- Hvad er dragefirkantens areal?
Svar på opgave 3:
-
Nedenunder er tegnet et eksempel på en dragefirkant, der opfylder betingelserne. Udenom er tegnet et rektangel, hvis sider er samme længde som dragefirkantens diagonaler.

Det ses, at dragefirkantens areal er halvdelen af arealet af dette rektangel og dermed lig med halvdelen af diagonalernes produkt.
Dvs. dragefirkantens areal = 0,5·12·16 = 96 -
Summen af vinklerne i en firkant er 360°. De to resterende vinkler i denne dragefirkant er dermed tilsammen:
360° - (110° + 30°) = 360° - 140° = 120°.
Da de kendte vinkler er forskellige, så må de to sidste være ens.
Dvs. de må hver være halvdelen af 120°, som er lig med 120°/2 = 60° -
Diagonalen AC er hypotenusen i den retvinklede trekant ABC. Dette er vist nedenfor.
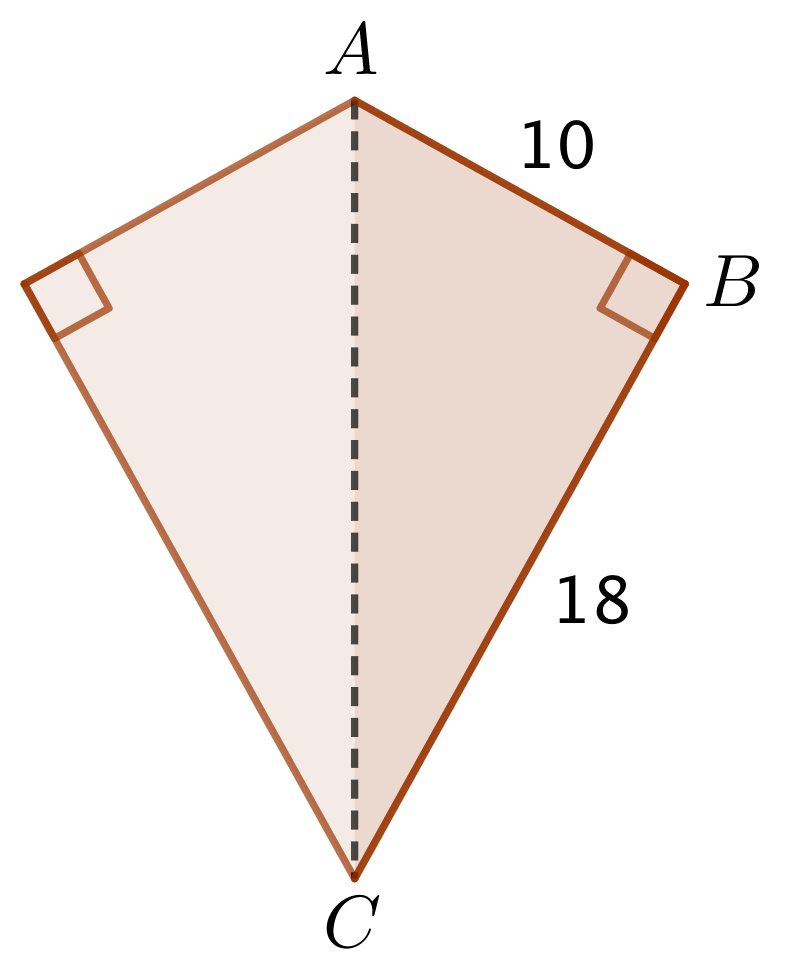
Her kan |AC| findes ved hjælp af Pythagoras læresætning:
|AC|2 = |AB|2 + |BC|2 ⇒
|AC|2 = 102 + 182 ⇒
|AC|2 = 424 ⇒
|AC| = √424 = 20,5913 = 20,6 -
Arealet af dragefirkanten er |AB|·|BC| = 10·18 = 180
Forklaring: Man kan dele dragefirkanten i to ens retvinklede trekanter langs den ene diagonal. Disse retvinklede trekanter kan sættes sammen til et rektangel med siderne 10 og 18. Da rektanglet har samme areal som dragefirkanten, så er dragefirkantes areal lig med 180. Dette er vist nedenunder.

Opgave 4. Ligebenet trekant. (Geometri III).
En ligebenet trekant har to ens sider kaldet ben og to ens vinkler. Den tredje vinkel kaldes topvinklen. Siden modsat topvinklen kaldes grundlinjen.

En ligebenet trekant har to ens sider kaldet ben og to ens vinkler. Den tredje vinkel kaldes topvinklen. Siden modsat topvinklen kaldes grundlinjen.

- Tegn en ligebenet trekant med benlængden 6 og grundlinjen 9.
- Hvad er topvinklen, hvis de to ens vinkler hver er 45°?
- Hvad er grundlinjen i en ligebenet trekant, hvis hvert ben har længden 7 og omkredsen er 20.
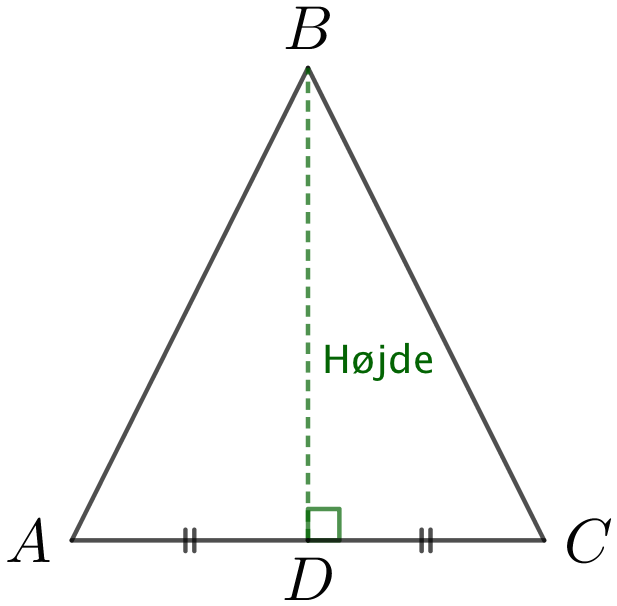
- Hvad er højden i toppunktet, hvis grundlinje er 6 og arealet er 24? Højden i topvinklen deler en ligebenet trekant i to ens retvinklede trekanter. Nedenunder er de to retvinklede trekanter ΔABD og ΔBCD.
- Hvad er længden af hvert ben, hvis grundlinjen er 16 og højden i toppunktet er 5?
- Hvad er arealet af en ligebenet trekant, hvis højden er 13 og benlængden er 15?
Svar på opgave 4:
-
Tegningen nedenfor er lavet i Geogebra.

-
Vinkelsummen i en trekant er 180°. De to ens vinkler er tilsammen 45° + 45° = 90°. Tilbage til topvinklen er 180° - 90° = 90°.
Dvs. topvinklen er 90° -
Omkredsen på 20 er summen af sidernes længder. Benene har hver længden 7, hvilket tilsammen er 14.
Dvs. grundlinjen er 20 - 14 = 6 -
Arealet af en trekant er 0,5·højde·grundlinje. Da arealet her er 24 og grundlinjen 6, så får man:
24 = 0,5·højde·6 ⇒ højde = 24·2/6 = 8. Dvs. højden i toppunktet er 8 -
Man skal finde |BC| i den retvinklede trekant BCD, hvor BC er hypotenusen. DB og CD er henholdsvis højde i toppunkt og halvdelen af grundlinjen i ΔABC.
Man skal bruge Pythagoras læresætning, der giver: |BC|2 = |BD|2 + |CD|2 = 52 + 82 = 25 + 64 = 89.
Dermed fås, at benlængde = √89 = 9,43 -
Arealet af ΔABC er 0,5·grundlinje·højde = |CD|·højde = |CD|·13.
Man skal bruge Pythagoras læresætning for at finde |CD|: |BC|2 = |BD|2 + |CD|2 ⇒ 152 = 132 + |CD|2 ⇒ |CD|2 = 152 - 132 = 225 - 169 = 56 ⇒ |CD| = √56 = 7,4833.
Dermed fås, at arealet af ΔABC er 7,4833·13 = 97,2829 = 97,3
Opgave 5. Terningkast. (Sandsynlighed).
- Hvad er sandsynligheden for at slå en sekser i et slag med en ærlig terning?
- Hvad er sandsynligheden for at få tre seksere i tre slag med en terning?
- Hvad er sandsynligheden for ikke at få nogen seksere i tre slag med en terning? Lav 100 simuleringer af tre terningkast i Excel.
- Hvad er sandsynligheden for at få mindst en seksere med en terning i følge disse simuleringer?
Svar på opgave 5:
- Sandsynligheden for en sekser er 1/6 = 0,167
- Sandsynligheden for tre seksere i træk er (1/6)·(1/6)·(1/6) = (1/6)3 = 1/216 = 0,0046
- Sandsynligheden for ikke at få en seksere i eet slag er 1 - 1/6 = 5/6. Sandsynligheden for ikke at få nogen seksere tre gange i træk er (5/6)·(5/6)·(5/6) = (5/6)3 = 125/216 = 0,58
-
Excelarket med simuleringer kan ses her: Excel-simulering. Kommandoerne, som er brugt, ses ved at markere de enkelte celler i Excel-arket.
Antallet af forsøg, hvor der er mindst 1 sekser, er fremhævet med rødt. Dette tal skal divideres med 100 for at få sandsynligheden for at få mindst en sekser i tre forsøg. Hvis man trykker F9 eller skriver noget i en tilfældig tom celle og trykker Enter, så vil man få 100 nye simuleringer. (Dette kaldes at opdatere simuleringerne.)
Det ses, at antallet af forsøg, der giver mindst en sekser varierer meget fra den ene opdatering til den næste, så 100 simuleringer er ikke nok til at bestemme sandsynligheden. Ved at opdatere 10 gange og tage gennemsnittet, så får man ca. 42 forsøg med mindst en sekser, hvilket giver en sandsynlighed på 0,42.
Opgave 6. Frugtsaft. (Købmandsregning).
Firmaet A presser frugt til frugtsaft. Nogle af dets priser er vist.
Firmaet A presser frugt til frugtsaft. Nogle af dets priser er vist.
| Antal kg frugt | Pris i kr. |
| 0 - 9 | 50 |
| 10 - 19 | 100 |
| ... | ... |
| 50 - 59 | 300 |
- Udfyld skemaet.
- Hvad koster det at få presset 35 kg frugt? 10 kg frugt giver 5 L saft.
- Opskriv en formel for hvor manger liter saft, som man kan få af x kg frugt. Firmaet B presser også frugt. De tager 100 kr i startgebyr plus 2 kr pr. kg frugt. Man kan også højst få presset 60 kg frugt hos firma B.
- Hvilket firma er billigst, hvis man skal have presset 24 kg frugt?
- Lav en graf der viser, hvornår firma A er billigst og hvornår firma B er. Første-aksen er antal kg frugt og anden-aksen er prisen for at få frugten presset. Grafen skal kun give et overblik, man behøver ikke at kunne aflæse de præcise tal.
Svar på opgave 6:
-
Nedenfor er tabellen udfyldt.
Antal kg frugt Pris i kr. 0 - 9 50 10 - 19 100 20 - 29 150 30 - 39 200 40 - 49 250 50 - 59 300 -
Det fremgår af tabelllen, at det koster 200 kr at få presset 30 - 39 kg frugt.
Derfor koster det 200 kr at få presset 35 kg frugt. -
Man opskriver en formel med ord:
Antal liter saft = (antal liter saft pr. kg frugt)·(antal kg frugt).
Fra opgaveteksten får man:
Antal liter saft pr. kg frugt = (5 L)/(10 kg) = 0,5 L/kg.
Antal kg frugt = x.
Dette giver: Antal liter saft = 0,5·x, hvor x er frugtens vægt i kg. -
Hos firma A koster det 150 kr, at få presset 24 kg frugt. (24 ligger mellem 20 og 29).
Hos firma B koster det 100 kr + (24 kg)·(2 kr/kg) = 148 kr, at få presset 24 kg frugt.
Dvs. firma B er billigst -
Nedenunder er vist en graf, hvor den sorte trappeformede kurve viser prisen for firma A, mens den stiplede linje viser prisen B.
Rødt viser hvornår A er billigst og blå farve viser hvornår B er billigst.
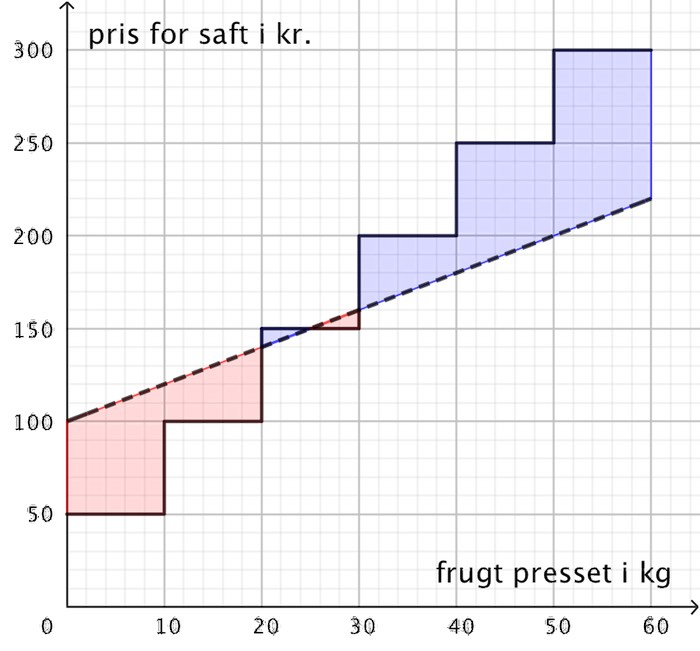
A er billigst mellem 0 og 20 kg og igen mellem 25 og 30 kg. B er billigst mellem 20 og 25 kg og igen mellem 30 og 60 kg.
Kurverne skærer hinanden for antal kg frugt lig med 20, 25 og 30. Man kan ikke af grafen se, hvilket firma som er billigst for præcis disse mængder, det kræver en beregning.
Opgave 7. (Regning med bogstaver, algebra).
Et tal kaldes a. Lad b være 1 mindre end a. Besvar følgende ved hjælp af a, tal og de fire regningsarter eller blot et enkelt tal:
Et tal kaldes a. Lad b være 1 mindre end a. Besvar følgende ved hjælp af a, tal og de fire regningsarter eller blot et enkelt tal:
- Hvad er b?
- Hvad er a - b?
- Hvad er (a - b)2? Tag et helt tal c og læg det dobbelte til. Træk herfra det halve af det, som man er nået til.
- Hvad får man ud af dette udtrykt ved c og et tal?
Svar på opgave 7:
- Man får: b = a - 1
- Man får: a - b = a - (a - 1) = a - a + 1 = 1
- Man får: (a - b)2 = 12 = 1
- Man får: c + 2·c - 0,5·(c + 2·c) = 3·c - 0,5·3·c = 1,5·c
Opgave 8. Trappefigur. (Figurfølge).
Nedenunder ses starten af en følge af trappefigurer.
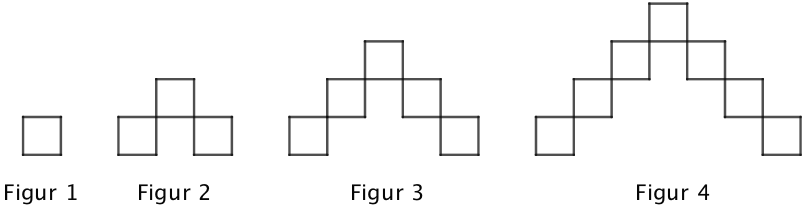
Nedenunder ses starten af en følge af trappefigurer.

- Hvor mange små kvadrater skal man lægge til en figur for at komme til den næste?
- Hvor mange små kvadrater skal der være i figur 5, hvis man fortsætter på denne måde?
- Hvor mange små kvadrater skal der være i figur n?
Svar på opgave 8:
-
Der skal lægges to små kvadrater til en figur for at komme til den næste som vist nedenunder.
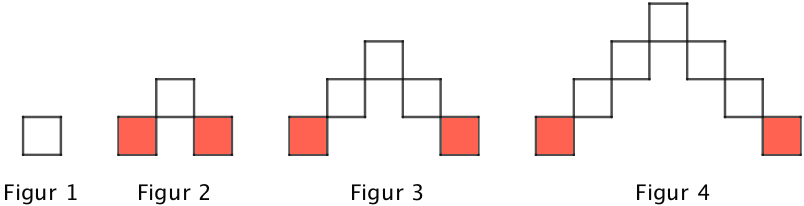
- Der skal være 9 kvadrater i figur nummer 5.
-
Man kan dele trappen op i to dele, hvor den ene indeholder n trin og den anden indeholder een færre.
Dvs. at antallet kvadrater i figur n er: n + (n - 1) = 2·n - 1
Nedenfor er fremgangsmåden vist med n = 4 som eksempel.

Det ses, at venstre del (fremhævet med fed) indeholder n kvadrater, mens den højre indeholder n - 1.