Svar på opgave 1: I praktik i en boghandel

1. Mie skal give 200,00 kr. - 132,50 kr. = 67,50 kr. tilbage
2. Mie skal taste 725,50 kr. + 500,00 kr. = 1225,50 kr. ind på dankortterminalen.
3. Kunden skal betale: 189,95 kr. · 0,80 = 151,96 kr. for ungdomsbogen.
4. Det rigtige udtryk er p·0,8. Det ses, at: a) er lig med dette udtryk og b) kan omskrives til det, idet: p - p·(20/100) = p·(1 - 0,20) = p·0,8. De andre kan ikke. Dermed er a) og b) de rigtige svar.

Svar på opgave 2: I praktik som murer

1. Arealet af sidefladen er (7,00 m)·(1,4 m) = 9,80 m²
2. Der skal bruges ca. 2·(66 mursten/m²)·(9,80 m²) ≈ 1294 mursten
3. Der skal bruges: 25·8 kg = 200 kg kalkmørtel.
4. Der skal bruges (15/6) L = 2,5 L cement. Dette vejer: (1/0,9 kg/L)·(2,5 L) = 2,78 kg, som er mængden af cement, der skal bruges for hver sæk kalkmørtel.

Svar på opgave 3: I praktik som journalist

1. Den største forskel er i 2014. Den er på: 86.683 - 49.218 = 37.465 personer
2. Værdiakserne er ikke ens. Den ene starter ved 0 og den anden ved 50.000.
3. Graf i Excel.
   
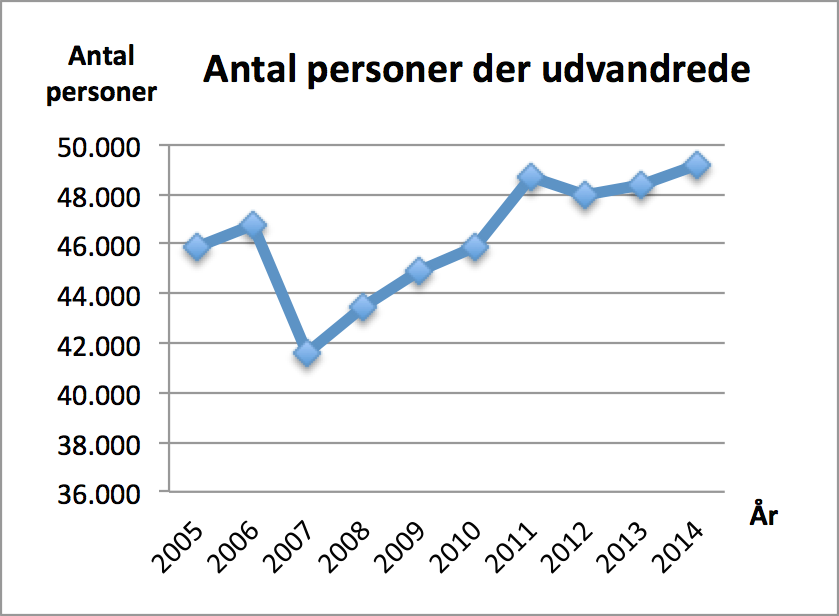
4. Der er en stigning i antallet af indvandrere fra 2005 til 2008. Dernæst sker et fald fra 2008 til 2009 og derefter sker igen en stigning. I alt var der 65 % flere indvandrere i 2014 end i 2005. Antallet af udvandrere steg fra 2005 til 2006, men faldt igen 2006 til 2007. Herefter steg antallet fra 2007 til 2014. I alt var der 7 % flere udvandrere i 2014 end i 2005.

Svar på opgave 4: I praktik som arkitekt

1. To cirkler tegnes i Geogebra med A og C som centrum og radius |AC|. De to cirkler skærer hinanden i punktet B.
   
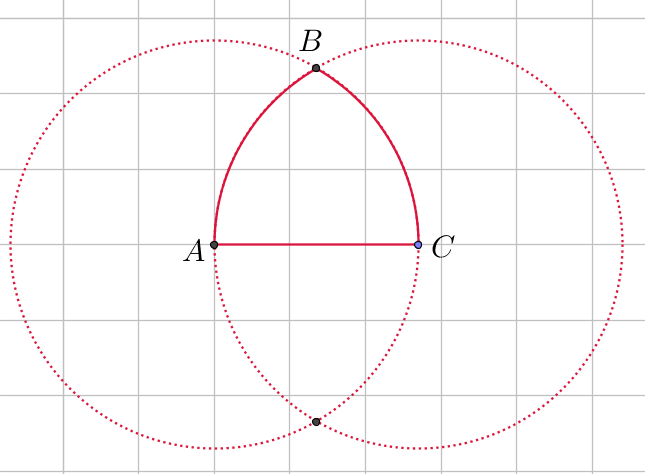
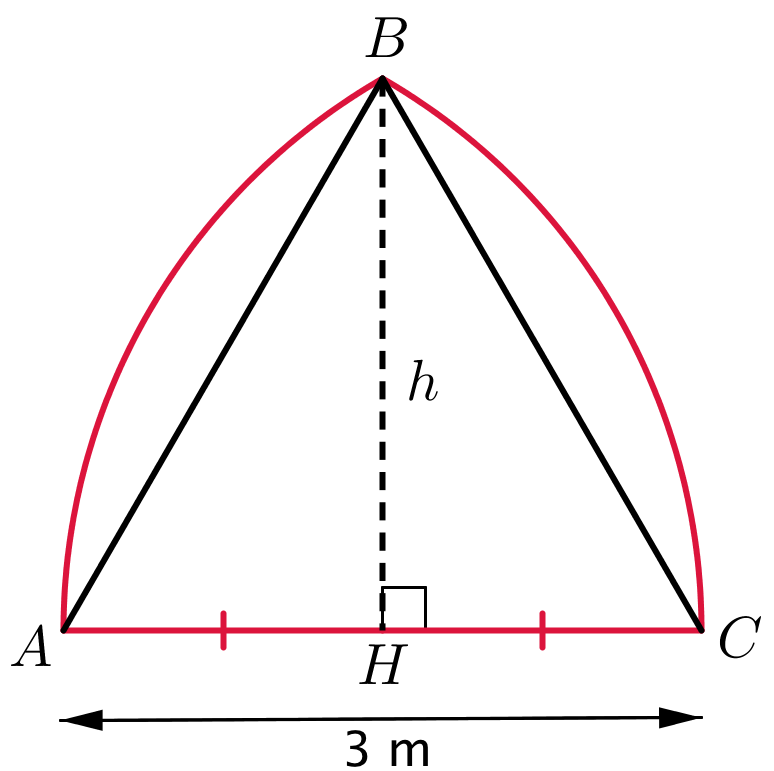
2. |AC| = 3 m. Det ses af tegningen, at |AH| = 0,5·|AC| = 1,5 m. Ved hjælp af Pythagoras læresætning får man:
   h² + |AH|² = |AC|² ⇒
   h² + (0,5·|AC|)² = |AC|² ⇒
   h² = 3² - (3/2)² ⇒
   højden = √(6,75) = 2,60 m
   
3. Man skal finde |AC|, som er lig med |BC|. I følge Pythagoras' læresætning gælder:
   h² + (0,5·|AC|)² = |BC|² ⇒
   h² + (0,5·|AC|)² = |AC|² ⇒
   4² = |AC|² - 0,5²·|AC|² ⇒
   16 = 0,75·|AC|² ⇒
   |AC| = √(16/0,75) = 4,62. Det vil sige, at portens bredde er 4,62 m

Svar på opgave 5: Sekskanter

1. Omkredsen af figur nr. 5 er 6·5 = 30
2. Omkredsen af figur nr. n er 6·n
3. Graf for antallet af enhedstrekanter.
   
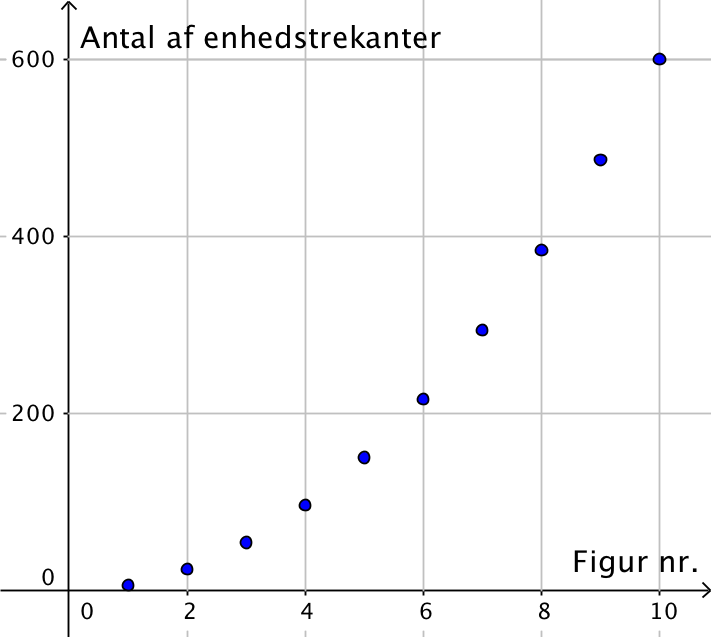
4. Figur nummer 9 indeholder 6·9² = 6·81 = 486 enhedstrekanter.
5. Man skal finde det hele tal n, der gør, at 6·n² > 1000. Man får:
   6·n² = 1000 ⇒
   n = √(1000/6) = 12,9.
   Det vil sige, at n skal være større end 12

Svar på opgave 6: Retvinklede og ligesidede trekanter

1. Det følger af Pythagoras' læresætning:
   c² = a² + b² ⇒
   c² = 4² + 3² ⇒
   c = √(16 + 9) = 5
2. Tegning i Geogebra.
   
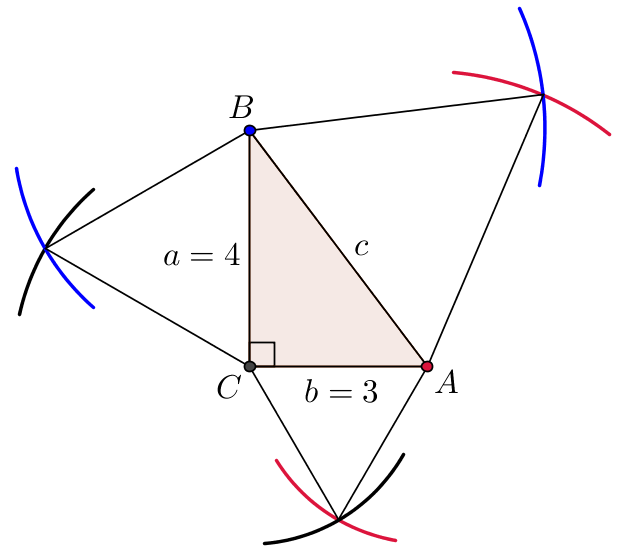
3. Arealet af en ligesidet trekant er s²·√3/4, s er sidelængden i trekanten. Arealerne af de tre ligesidede trekanter i opgaven er:
   a²·√(3)/4 = (16/4)·√(3),
   b²·√(3)/4 = (9/4)·√(3) og
   c²·√(3)/4 = (25/4)·√(3)
   Summen af arealerne af de to mindste ligesidede trekanter er: (25/4)·√(3). Dermed er summen af de små ligesidede trekanters arealer lig med arealet af den store.
4. Den gælder f.eks. ikke for den nedenstående trekant. Her er summen af arealerne af de små ligesidede trekanter = 4,7 + 6,93 = 11,63, der er forskellig fra 15,59, som er arealet af den store ligesidede trekant.
   
5. Fra spørgsmål 3 har man, at summen af de to små ligesidede trekanter er: a²·√(3)/4 + b²·√(3)/4 = (a² + b²)·√(3)/4. Arealet af den store ligesidede trekant er c²·√(3)/4.
   Da ΔABC er retvinklet, så gælder at a² + b² = c². Dermed er summen af de små ligesidede trekanters arealer lig med den stores.