Svar på opgave 1: Gustavs svømmetræning

1. Han svømmer 1,5 timer 4 dage om ugen, det vil sige: 1,5·4 timer = 6 timer i alt
2. Han svømmer 600 m/(25 m/bassinlængde) = 24 bassinlængder
3. Antal pulsslag pr. minut: 31 pulsslag/(10/60 minut) = 31·6 pulsslag/min. = 186 pulsslag/min. Han puls er dermed 186
4. Hans maksimale puls skal ligge mellem 0,70·204 = 142,8 og 0,75·204 = 153. Omregnet til pulsslag på 10 sek. er det: 142,8/6 = 23,8 og 153/6 = 25,5. Det vil sige, at antallet af pulsslag skal ligge mellem: 23,8 og 25,5.
5. Hans gennemsnitsfart er 100 m/(57,6 sek.) = 100·(0,001 km)/[57,6 (1/3600) time] = 360/57,6 km/t = 6,25 km/t. Det vil sige, at gennemsnitsfarten ved crawl er større end 5 km/t.

Svar på opgave 2: Gustavs klasselokale

1. Arealet er 22·6 m³ + 12 m³ = 144 m³
2. Tegning i Geogebra.
   
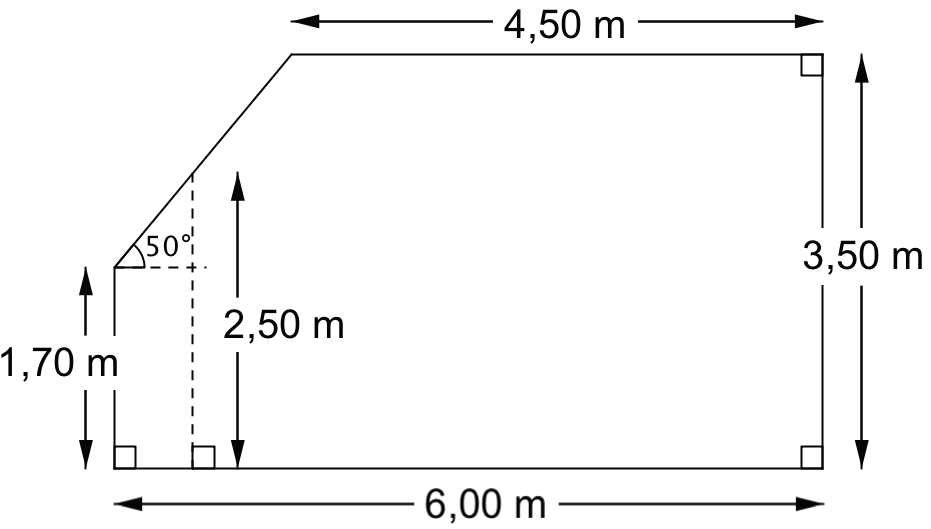
3. Af den blå retvinklede trekant på tegningen nedenunder fremgår det, at tan(50°) = (modstående katete)/(hosliggende katete) = (0,8 m)/x ⇒ x = (0,8 m)/tan(50°) = (0,8 m)/1,1918 = 0,67 m
   
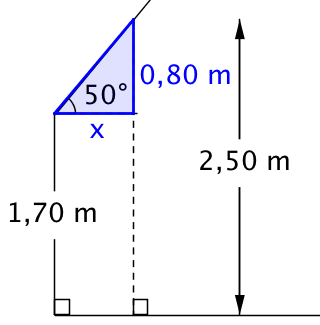
4. Den del af rummet der har mere end 2,5 meters loftshøjde kan inddeles i tre stykker vist med blå, rød og grøn. Tykkelsen af det røde område er (6,00 m - 4,50 m) - 0,67 m = 0,83 m.
   
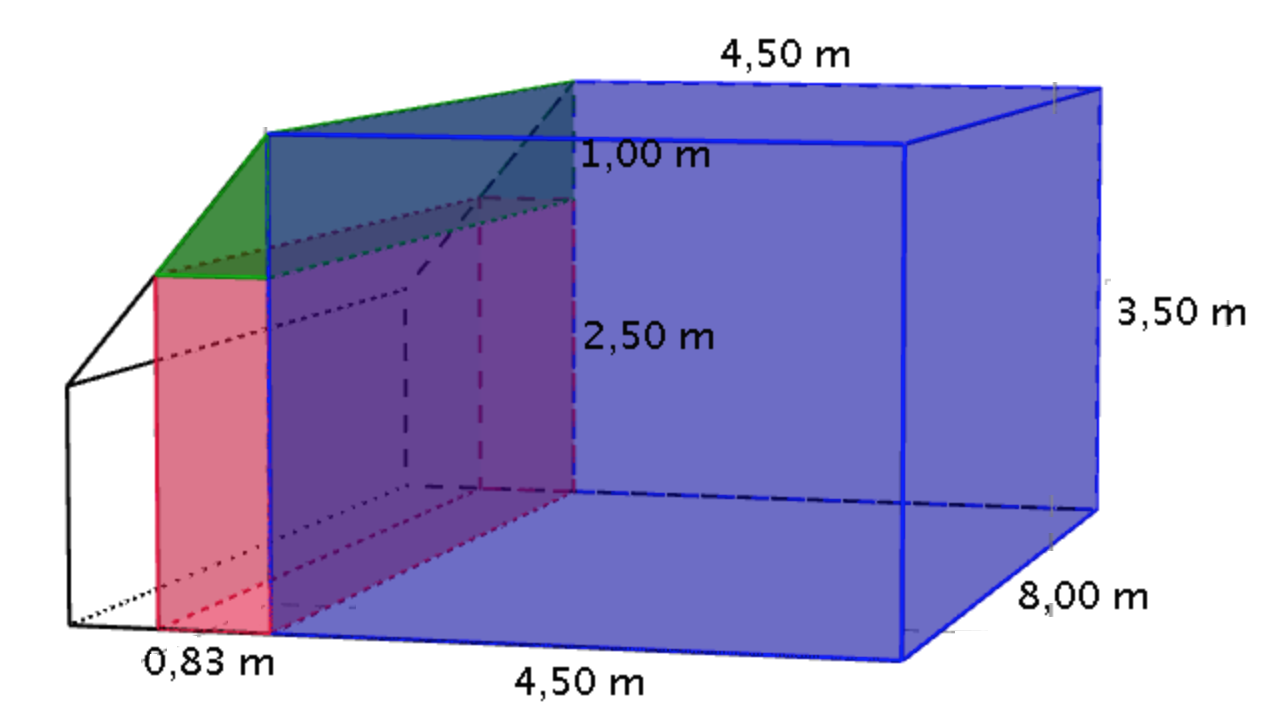
   Rumfanget af det blå område er 4,50 m · 3,50 m · 8,00 m = 126 m³. Rumfanget af det røde område er 0,83 m · 2,50 m · 8,00 m = 16,6 m³. Rumfanget af det grønne område er 0,5 · 8,00 m · 0,83 m · 1,00 m = 3,32 m³. Tilsammen giver det rumfanget: 126 m³ + 16,6 m³ + 3,32 m³ = 145,9 m³.
   Det vil sige der er plads til klassen i rummet

Svar på opgave 3: Gustavs højde

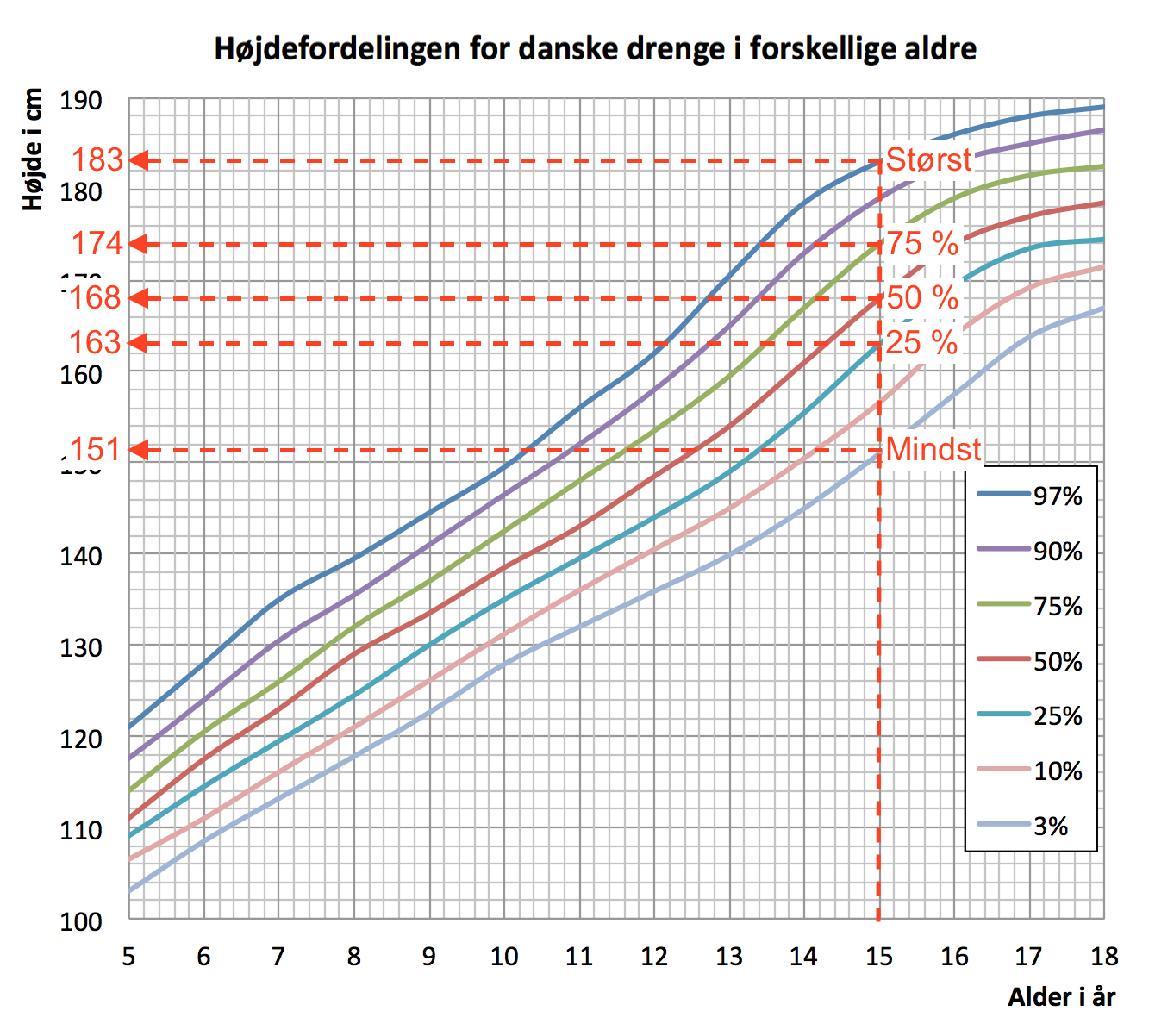
1. Man får i følge formlen at Gustavs sluthøjde er ((189 cm + 167 cm)/2 + 6,5 cm) ± 8,5 cm = 184.5 cm ± 8,5 cm. Det vil sige, at Gustavs forventede sluthøjde er mellem 176 cm og 193 cm
2. Han ligger på 75 %-kurven, hvilket kan ses af nedenstående figur. Han kan derfor forvente at ende på en højde af 183 cm som 18-årig.
   
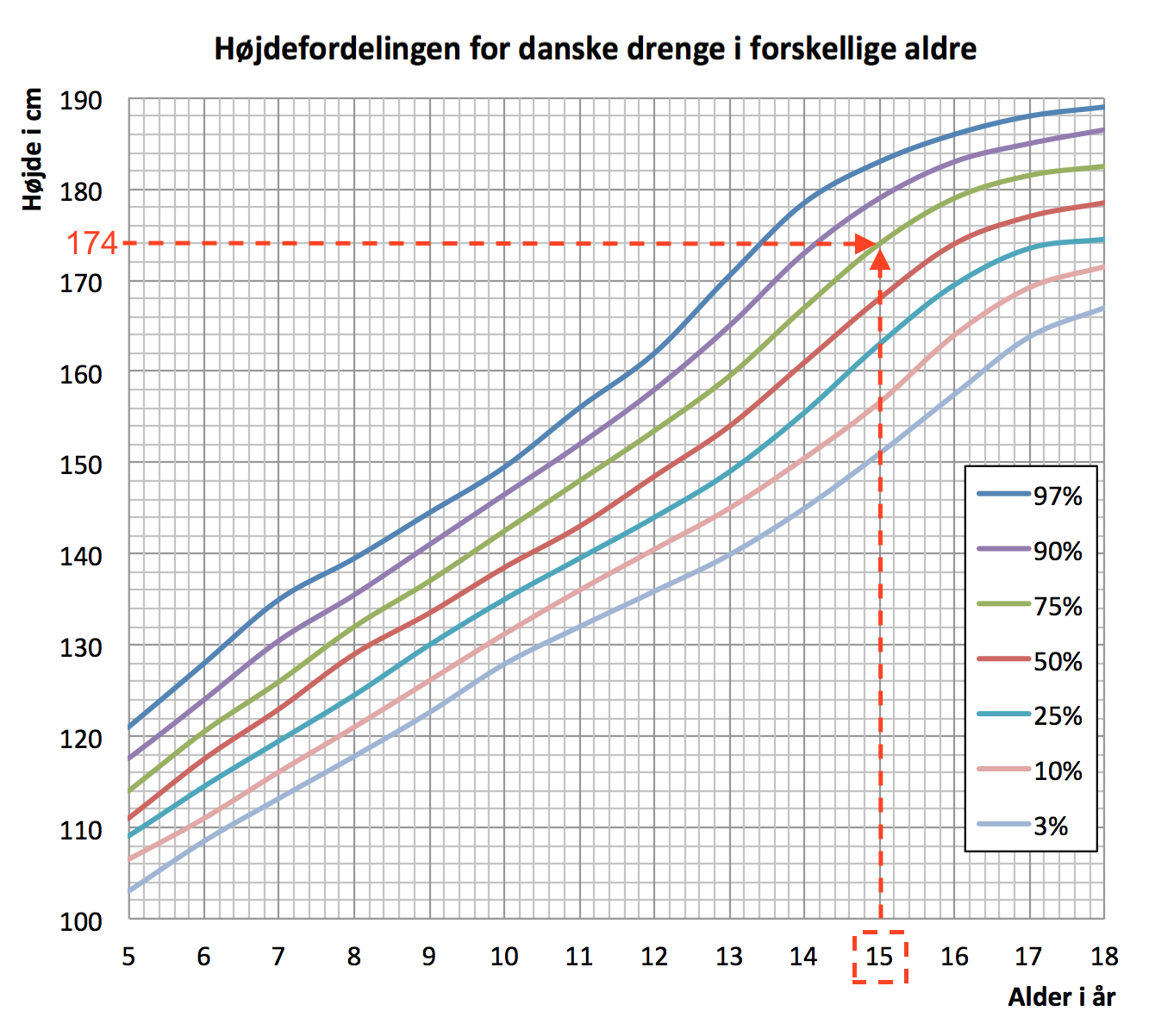
3. Da han ligger på 75 %-kurven, hvilket betyder, at 75 % på hans alder er mindre end ham, og dermed er 25 % større end ham.
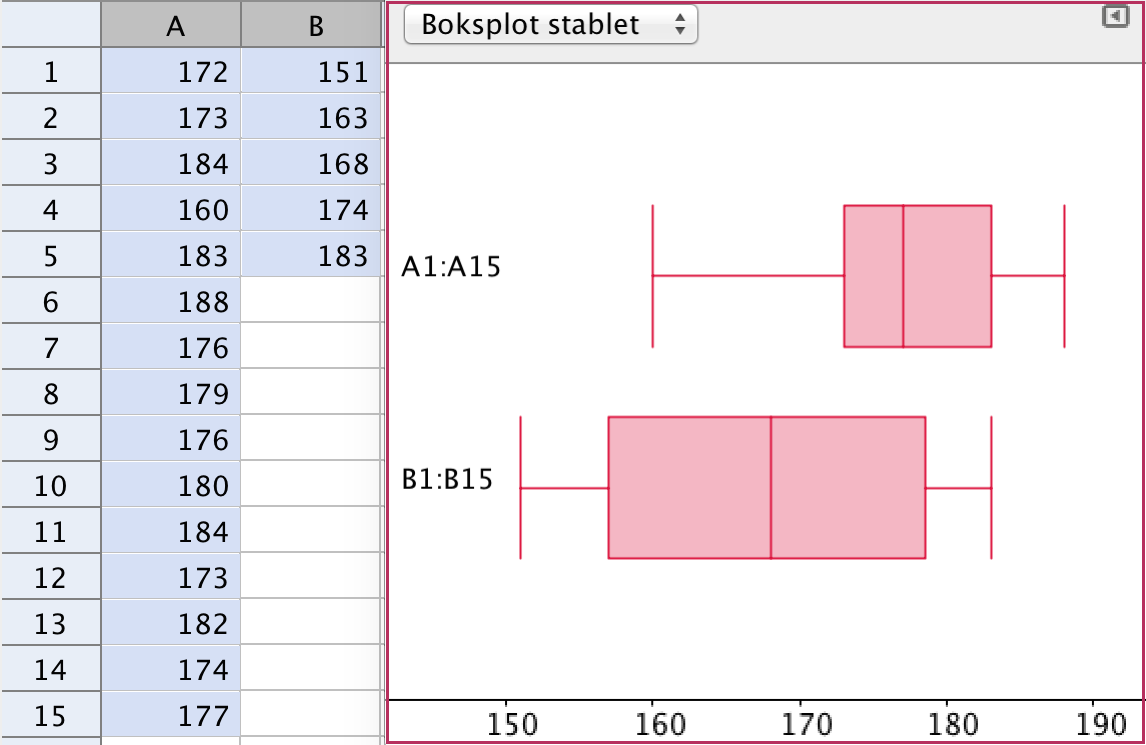
4. Man sorterer observationssættet efter størrelse og får: 160, 172, 173, 173, 174, 176, 176, 177, 179, 180, 182, 183, 184, 184, 189 og markerer det midterste tal. Det ses at være 177 cm og medianen er dermed 177 cm. Medianen er den højde som halvdelen af drengene i klassen ligger under.
5. Nedenstående figur viser hvordan man aflæser kvartilsættet for 15-årige drenge for hele landet. Man vælger 3 %- og 97 %-kurven som yderpunkter til boksplottet.
   
   Nedenstående figuren er lavet i Geogebra. De aflæste tal er vist (næstyderst til venstre) på nedenstående figur sammen med tallene for Gustavs klasse (yderst til venstre). Der er to boksplot på figuren, det øverste er for Gustavs klasse og den nederste er for hele landet. Gennemsnittet for Gustavs klasse ligger over landsgennemsnittet for 15-årige.
   

Svar på opgave 4: Gustavs knallert

1. Han bruger 100 km /(25 km/liter) = 100/25 liter = 4 liter
2. Man ser kun på udgiften til benzin. Af tabellen over de samlede udgifter ses, at Gustavs udgifter stiger med 5 kr. for hver 10 km eller 0,50 kr./km, som han kører ekstra. For 150 km svarer det til 150 km·0,50 kr./km =
   75 kr.
3. Stigningstallet findes ved at tage to y-værdier på kurven og trække dem fra hinanden. Dette tal divideres med forskellen mellem de tilsvarende x-værdier. Man tager her startværdierne: x = 0; y = 9500 og slut­værdierne: x = 16000; y = 17600. Stigningstallet bliver: [(17500 - 9500) kr.]/[(16000 - 0) km] = 0.50 kr./km
4. Maltes samlede udgifter er udgifter til knallert + udgifter til benzin. Udgiften til knallerten er konstant 11.500 kr., den ændrer sig ikke med tiden eller med antal køret kilometer. For hver km Malte kører bruger han 1/37,5 liter benzin. Det koster (12,50 kr.)/(37,5 km) = 1/3 kr./km.
   Idet man sætter x = antal km, som Malte kører, finder man følgende sammenhæng mellem hans samlde udgifter og antal kørte km: x·1/3 kr./km. + 11.500 kr.
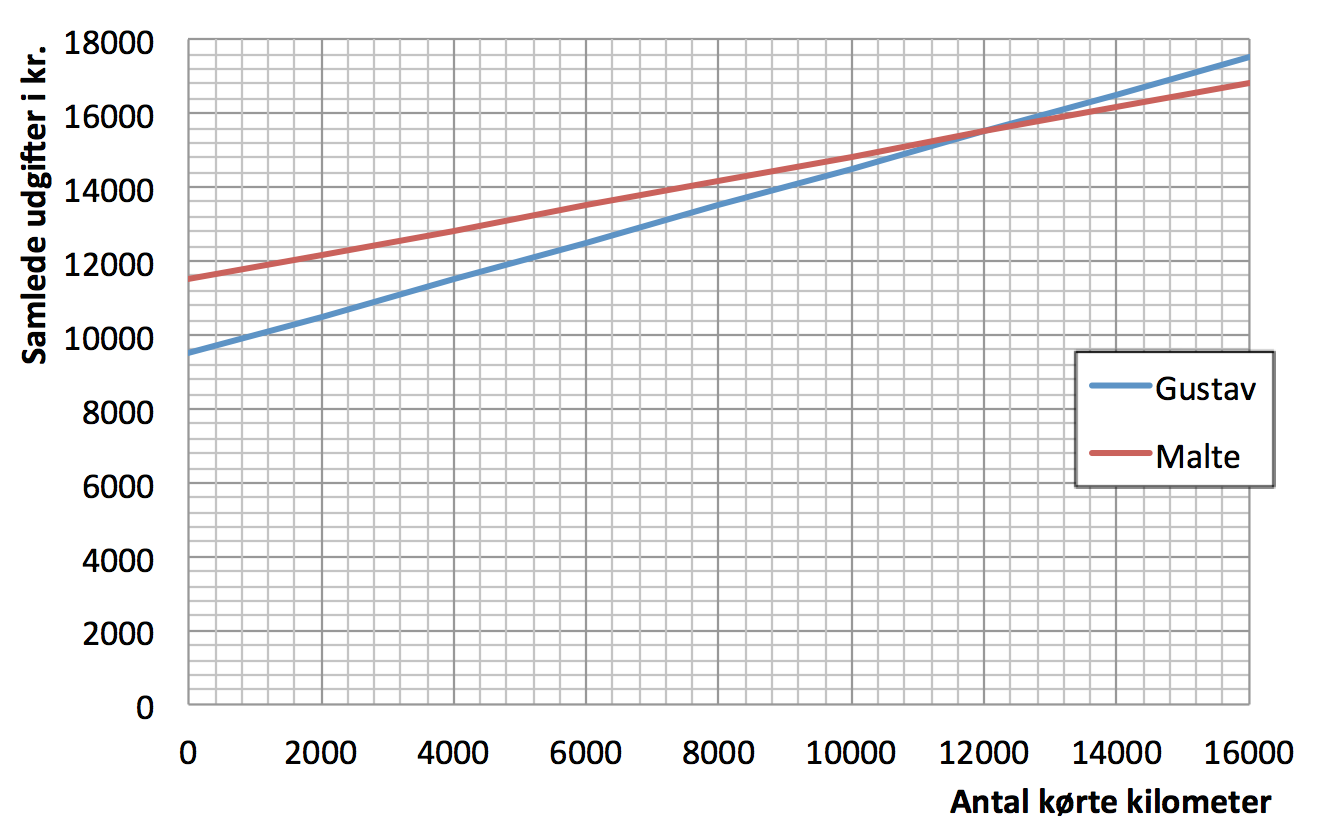
5. Grafen viser Maltes samlede udgifter i samme graf som Gustavs.
   
6. Det ses at graferne i besvarelsen af opgave 5 skærer hinanden for antal kørte kilometer lig med 12.000, og at Gustavs kurve ligger over Maltes derefter. Da begge brødre kører 5.000 km om året svarer det til, at Gustavs samlede udgifter overstiger Maltes efter 2,6 år og derfor også efter 3 år.
   Heraf ses, at Malte har ret.

Svar på opgave 5: En ligesidet trekant

1. Omkredsen er 3·6 = 18
2. Arealet af en ligesidet trekant er: siden i anden gange (√3)/4 = 6²·(√3)/4 = 9·√3 = 15,6
3. Hver trekant er retvinklet og den ene vinkel er 60°, da den er den samme som i den ligesidede trekant. Den sidste vinkel er derfor 30° (= 180° - 90° - 60°). Vinklerne er derfor: 30°, 60° og 90°
4. Hypotenusen er lig med siden i den ligesidede trekant og den korteste katete er halvdelen af siden i den ligesidde trekant. Derfor er den korteste katete halv så stor som hypotenusen i den retvinklede trekant.
5. Den længste katete findes ved hjælp af Pythagoras læresætning. Den længste katetes længde kaldes x. Der gælder:
   x² + (0,5·6)² = 6² ⇔ x² = 6² - (0,5·6)² ⇔
   x² = 36 - 3² ⇔ x² = 36 - 9 ⇔ x² = 27 ⇒ x = 5,20
6. Det udledes ved hjælp af Pythagoras læresætning. Hypotenusen kaldes c og den længste katete for b. Den korteste katete kaldes a. Man skal vise, at: b = a·√3.
   Der gælder at c = 2·a. Man får:
   a² + b² = c² ⇔ a² + b² = (2·a)² ⇔
   a² + b² = 4·a² ⇔ b² = 4·a² - a² ⇔
   b² = 3·a² ⇒ b = a·√3, hvilket man skulle bevise.