Svar på opgave 1: På indkøb

1. Tre liter kakaomælk koster 3·11,50 kr. = 34,50 kr.
2. Literpris med tilbud er 25 kr./2 L = 12,50 kr./L.
   Literpris uden tilbud er 16,95 kr./2 L = 16,95 kr./L.
   Han sparer: 16,95 kr. - 12,50 kr. = 4,45 kr.
3. Kilopris for Top Smør: 13,95 kr./0,250 kg = 55,80 kr./kg
   Kilopris for Smør Let: 11,50 kr./0,200 kg = 57,50 kr./kg
   Det viser, at kilopriserne er rigtige
4. Tilbudspris = førpris·(100 % - rabat i %) ⇒
   Førpris = tilbudspris / (100 % - rabat i %) = 19,95 kr./(1 - 0,40) = 19,95 kr./0,60 = 33,25 kr.

Svar på opgave 2: En redekasse (tegninger lavet i Geogebra)

1. 7 stykker: topstykke, bundstykke, forside, bagside, 2 endeplader og midterpladen.
2. Nedenfor er en tegning af udskæringer. De to plader er, som det ses, nok til at bygge redekassen, da udskæringerne kan være inden for de to plader.
   
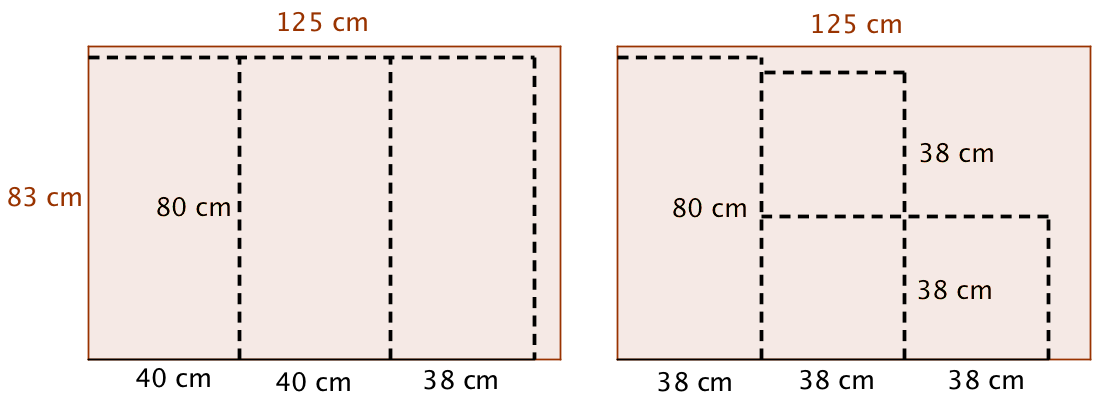
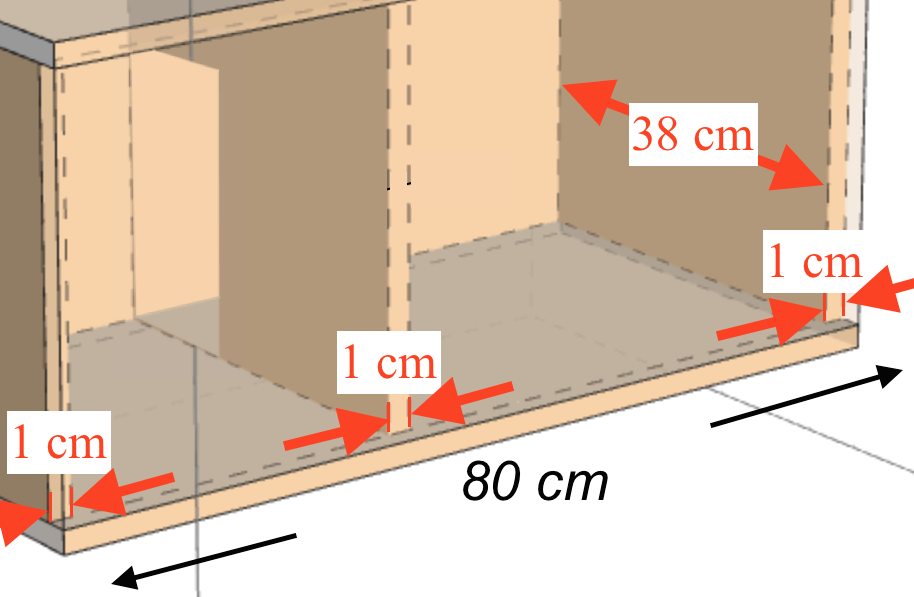
3. Bundpladen er 80 cm i længden. Herfra skal trækkes tykkelsen af de to endestykker og midterpladen på hver 1 cm. I alt skal der trækkes 3 cm fra 80 cm for at få den indvendige længde.
   Bredden af bundpladen er 40 cm. Herfra skal trækkes tykkelsen af de to sideplader. I alt skal der trækkes 2 cm fra, så man får 38 cm i bredden indvendig i redekassen. Dette er vist nedenunder.
   Gulvarealet af redekassen (det indvendige areal af dens bund) er i alt: (80 - 3)·(40 - 2) cm² = 77·38 cm² = 2.926 cm².
   Der er også en døråbning med et gulv-areal på (38 - 25) cm gange 1 cm = 13 cm². Dette ses der bort fra.
   Dermed er der plads til : 2.926 cm²/(400 cm²/ugle) = 7,3 ugler. Dette skal rundes ned til nærmeste antal hele, hvilket giver: 7 ugler
   

Svar på opgave 3: Mikaels løbeture

1. Han løb i 24 minutter og han løb 5 kilometer
2. Han løb den første kilometer på 5 minutter. Hans gennemsnitshastighed er: (1 km) / (5/60 time) = 60/5 km/t = 12 km/t
3. Kurven kan se ud som vist nedenunder.
   
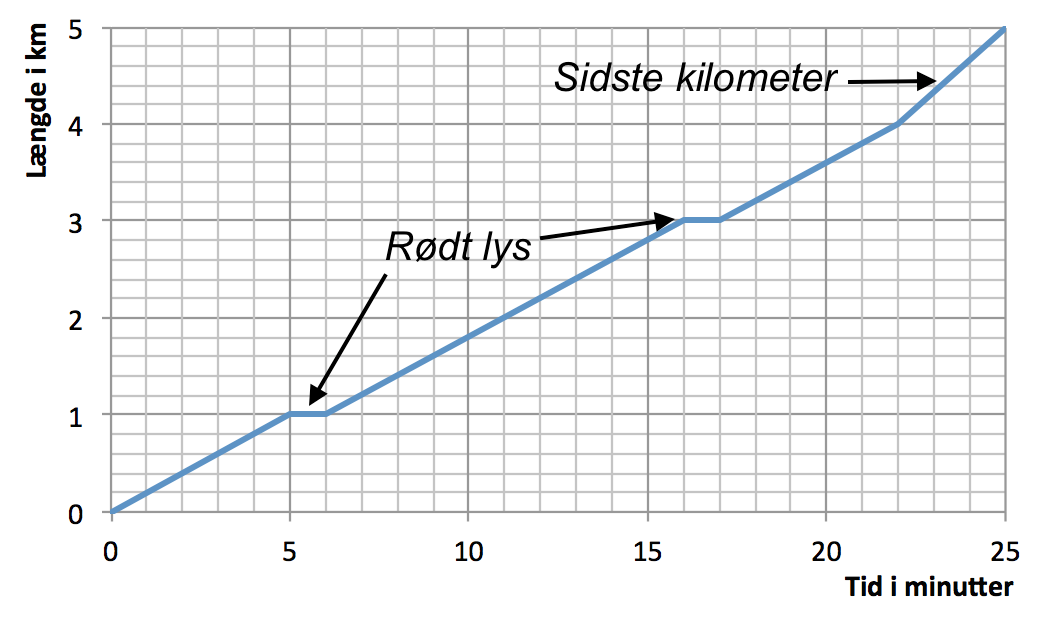
4. Kurven kommer til at se ud som vist nedenunder.
   
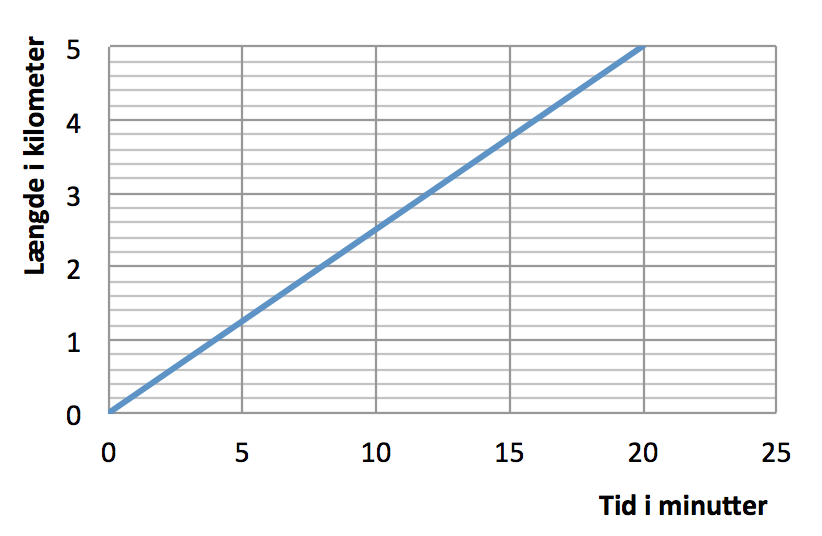
5. Den lineære sammenhæng kan skrives y = a·x + b, y er længden i kilometer og x er tiden i minutter. Konstanten a er hastigheden i kilomter pr. minut og b er startstedet, som vælges til 0. Man finder a ved formlen: a = gennemsnitshastighed = 5 km /20 minutter = 0,25 km/min.
   Det giver den lineære sammenhæng: y = 0,25·x

Svar på opgave 4: Brug af Facebook

1. Antallet af elever der bruger mindre end en time om dagen på Facebook er: 5 + 4 = 9
2. Der er i alt 22 elever i 9. A. Antallet af elever der er på Facebook mere end 2 timer om dagen er 2 + 1 + 1 + 2 + 4 = 10. Brøkdelen af klassen, som er på Facebook mere end 2 timer om dagen er 10/22 = 5/11
3. For begge klasser får man: Mindsteværdien er 0, størsteværdien er 4 og variationsbredden er 4
4. Mikael har ret i begge påstande. Man sætter de to klassers resultater ind i ét skema.
   
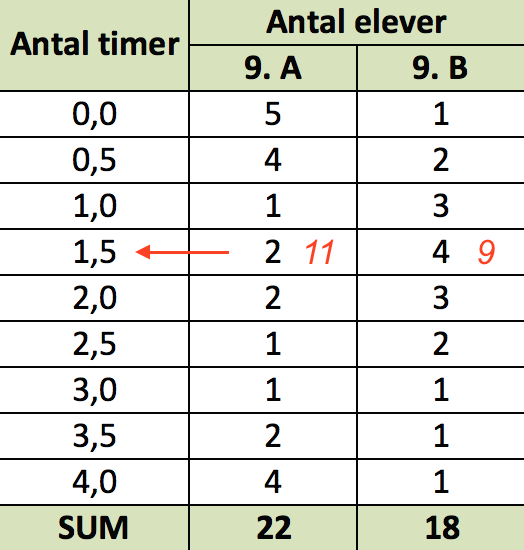
   De to røde tal viser, hvordan medianen beregnes: Der er 22 elever i 9. A - halvdelen af det er 11. Der er 18 elever i 9. B - halvdelen er 9.
   For begge klasser tæller man fra toppen indtil man når til halvdelen. For 9. A får man:
   0 timer: 5 elever
   0,5 timer: 4 elever, i alt 9 elever
   1,0 time: 1 elever, i alt 10 elever
   1,5 timer: 2 elever, i alt 12 elever.
   Det vil sige, at eleven med det 11. mindste forbrug, har et forbrug på 1,5 timer.
   For 9. B får man på samme måde, at den elev, der har det 9. mindste forbrug også er 1,5 timer på Facebook. Dermed er 1,5 timer medianen for begge klasser.
   Middelværdien for 9. A er : (1/22)·(0,0·5 + 0,5·4 + 1,0·1 + 1,5·2 + 2,0·2 + 2,5·1 + 3,0·1 + 3,5·2 + 4,0·4) = 1,75
   Middelværdien for 9. B er : (1/18)·(0,0·1 + 0,5·2 + 1,0·3 + 1,5·4 + 2,0·3 + 2,5·2 + 3,0·1 + 3,5·1 + 4,0·1) = 1,75
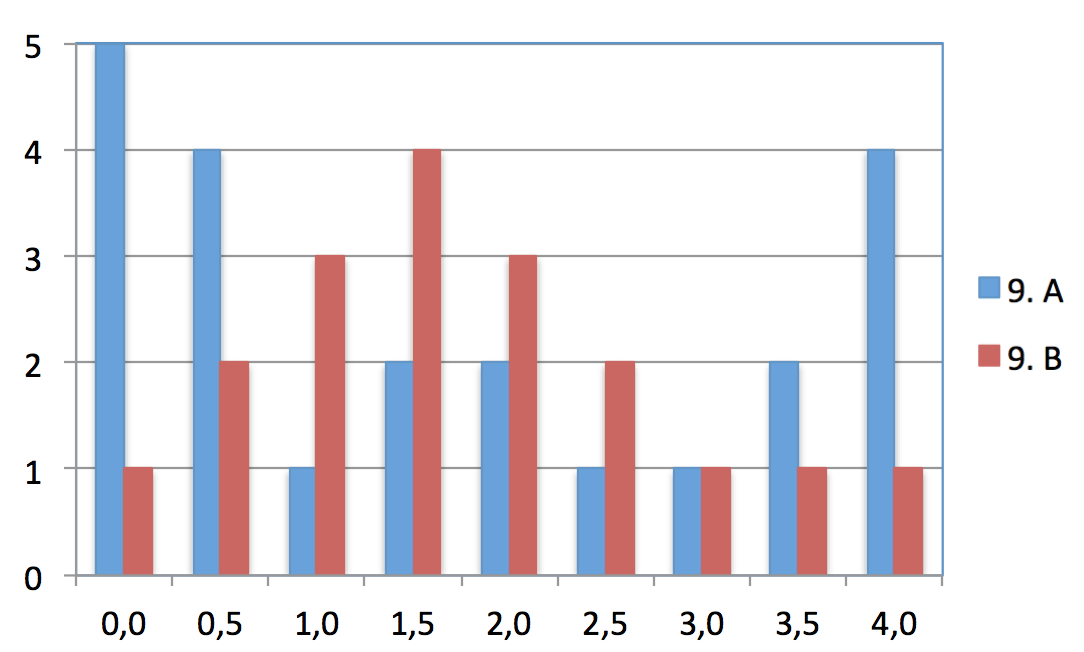
5. Man får nedenstående diagram. Det ses at 9. A ligger samlet om mindste og størsteværdierne, mens 9. B er samlet omkring middelværdien.
   

Svar på opgave 5: En femkantblomst

1. Alle vinkler er lige store og deres sum er 540°, derfor er den enkelte vinkel 540°/5 = 108°
2. Tegning af femkant i Geogebra.
   
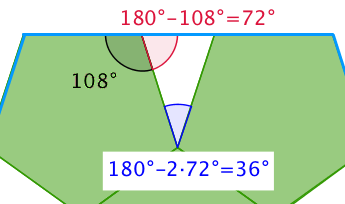
3. Den ligebenede trekants grundvinkel, v, er supplementvinkel til femkantens hjørnevinkel, det vil sige, at v = 180° - 108° = 72° Den ligebenede trekants topvinkel er dermed: 180° - 2·72° = 36°
   
4. Man ved at omridset er en regulær femkant, fordi alle dens sider er lige lange. De består nemlig af to sider fra den grønne femkant og en grundlinje fra en af de ligebenede trekanter.
5. Siden i blomsten er 2·5 + grundlinjen i den ligebenede trekant. Grundlinjen er lig med 2·5·sin(36°/2) = 2·5·sin(18°) = 2·1,55 = 3,1. Dette giver tilsammen sidelængden: 10 + 3,1 = 13,1, det vil sige, at Mikael har ikke ret
   

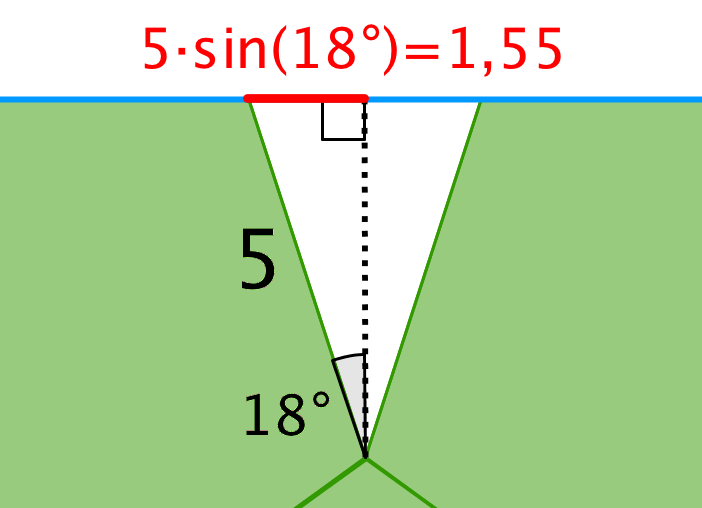
Svar på opgave 6: Sumtrekanter

1. Det bevises ved at gøre prøve. Hvis man indsætter 2 i det gule felt, skal der stå 3 i det røde og 9 i det grønne for at summerne i de to øverste cirkler skal stemme.
   Dermed stemmer summen i den nederste cirkel ikke med tallene i den røde og grønne firkant, og derfor kan der ikke stå 2 i den gule firkant
2. Opgaven kan løses ved at bruge tre ligninger med tre ubekendte, men man kan også prøve sig frem, da man ved, at der kun er tre muligheder for det gule felt.
   Det ses af, at summen af det gule og det røde felt skal give 5. Når man kun må bruge hele positive tal kan tallet i det gule felt kun være 1, 2, 3 eller 4 og 2 er udelukket efter den forrige delopgave.
   Prøver man sig frem får man, at det gule felt = 3, det røde felt = 2 og det grønne felt = 8
3. Summen af tallene i cirklerne giver: 8 + 12 + 16 = 36
   Summen af de firkantede felter giver: 2 + 6 + 10 = 18
   Da den første sum er dobbelt så stor som den sidste, stemmer Mikaels antagelse
4. Summen af tallene i cirklerne giver: (a + b) + (a + c) + (b + c) =
   a + b + a + c + b + c =
   (a + b + c) + (a + b + c) =
   2·(a + b + c)
   Summen af de firkantede felter giver: a + b + c
   Da den første sum er dobbelt så stor som den sidste, så stemmer Mikaels antagelse