Folkeskolens problemregning for 9. klasse, december 2012 | Gå til oversigt

Svar på opgave 1: Rejsekort til Emil

  1. Emil køber to billetter for hvert besøg. Han besøger Clara 4 gange. Antallet af billetter er i alt: 2·4 = 8.
    Pris for 8 billetter: 8·54,50 kr. = 436 kr.
  2. Han sparer 54,50 kr. - 30,00 kr. = 24,50 kr. pr. rejse
  3. Rejsekortets pris på 50 kr. skal lægges oven i prisen på 30 kr. pr. rejse. Man sætter antal rejser = x og får ligningen:
    50,00 kr. + x·30,00 kr. = x·54,50 kr. ⇔
    x = 50,00 kr./(54,50 kr. - 30,00 kr.) ⇔
    x = 2,04
    Det vil sige, at antallet skal være større end 2,04 og dermed bliver det mindste antal rejser, som Emil skal foretage, før det kan betale sig at bruge resekortet, lig med 3
  4. Ser man bort fra den faste omkostning på 50,00 kr. bliver den procentvise besparelse i forhold til normal pris på 54,50 kr.: 100 %·(54,50 kr. - 30,00 kr.)/54,50 kr. = 45 %. Det viser, at annoncen har ret.
  5. Han skal betale 5·30,00 kr. + 28,50 kr. = 178,50 kr. for de seks første rejser.
  6. Ved at prøve sig frem finder man, at 15 rejser koster 425 kr. og 20 rejser koster 545 kr. Man finder det præcise antal med nedenstående ligningen, hvor x er antallet af rejser over 15:
    425 kr. + x·26,50 kr. = 500 kr. ⇔
    x = (500 kr. - 425 kr.)/26,50 kr. ⇔
    x = 2,8
    Dette skal rundes ned til 2 for, at man skal holde sig under 500 kr. og antallet af rejser, der kan foretages for 500 kr. bliver derfor 15 + 2 = 17
  7. Grafen n er den rigtige. Den viser et forløb, hvor prisen stiger for hver rejse, men hvor stigningen i pris bliver mindre for hver femte rejse.
    Grafen m viser det man får, hvis man lægger priserne i nederste række af tabellen sammen for fem rejser ad gangen. Grafen l viser en faldende kurve, der ikke passer med noget.

Svar på opgave 2: Claras bueskydning

  1. Clara scorede i gennemsnit 174/36 point = 4.83 point
  2. Medianen på 4 fortæller at halvdelen af Claras pile var 4 point eller mindre.
  3. Boksplottene viser, at Clara er blevet bedre fra 2011 til 2012. Såvel medianen som de andre kvartiler er blevet bedre fra 2011 til 2012.

Svar på opgave 3: Emils akvarium

  1. Akvariet rumfang er 40 cm · 40 cm · 80 cm = 128.000 cm3 = 128.000 (0,1 dm)3 = 128.000·0,001 dm3 = 128 dm3 = 128 L
  2. Vi ved fra underopgave 1, at 1 L = 1.000 cm3.
    Længden ad vandet er 80 cm og bredden er 40 cm. Vandets højde kaldes x. Der gælder ligningen:
    80 cm · 40 cm · x = 120.000 cm3 ⇔
    x = 120.000 cm3/(80 cm · 40 cm) ⇔
    x = 37,5 cm
    Det vil sige, at vandets afstand til overkanten i akvariet er (40 - 37,5) cm = 2,5 cm
  3. Kuglen kan indeholde: (4/3)·π·r3 = (4/3)·π·(15 cm)3 = 14137,2 cm3 = 14,2 L
  4. Den indvendige radius kaldes x. Man har ligningen:
    (4/3)·π·x3 = 60.000 cm3 ⇔
    x3 = 60.000 cm3/[(4/3)·π] ⇔
    x3 = 14.323,9 cm3 ⇔
    x = 3√[14.323,9 cm3] ⇔
    x = 24,3 cm
    Det vil sige, at kuglens indvendige radius skal være 24,3 cm

Svar på opgave 4: Claras børneopsparing

  1. Claras forældre har indbetalt 12·250 kr. = 3.000 kr. om året.
  2. Clara var 36.000 kr./(3.000 kr./år) = 12 år
  3. Procentdelen, der udgøres af tilskrevne renter, var: 100 %·(42.698 kr. - 36.000 kr.)/42.698 kr. = 15.7 %
  4. Saldoen vil være: (42.698 kr.)·(1,02)6 = 48.085 kr.
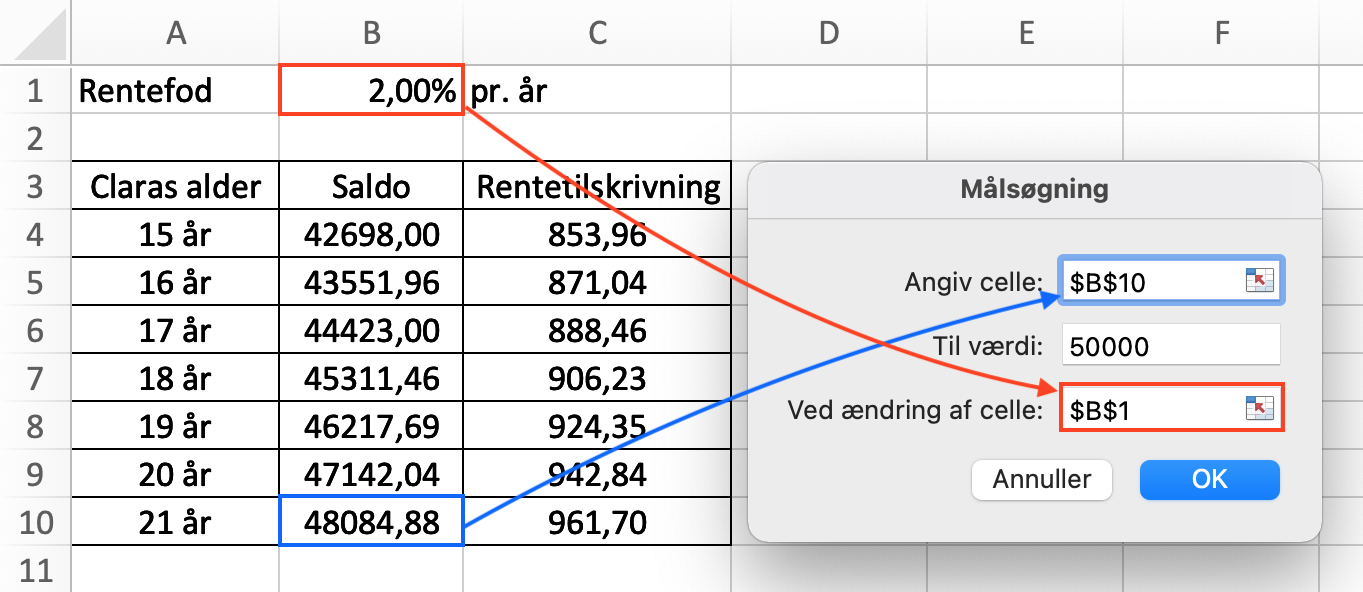
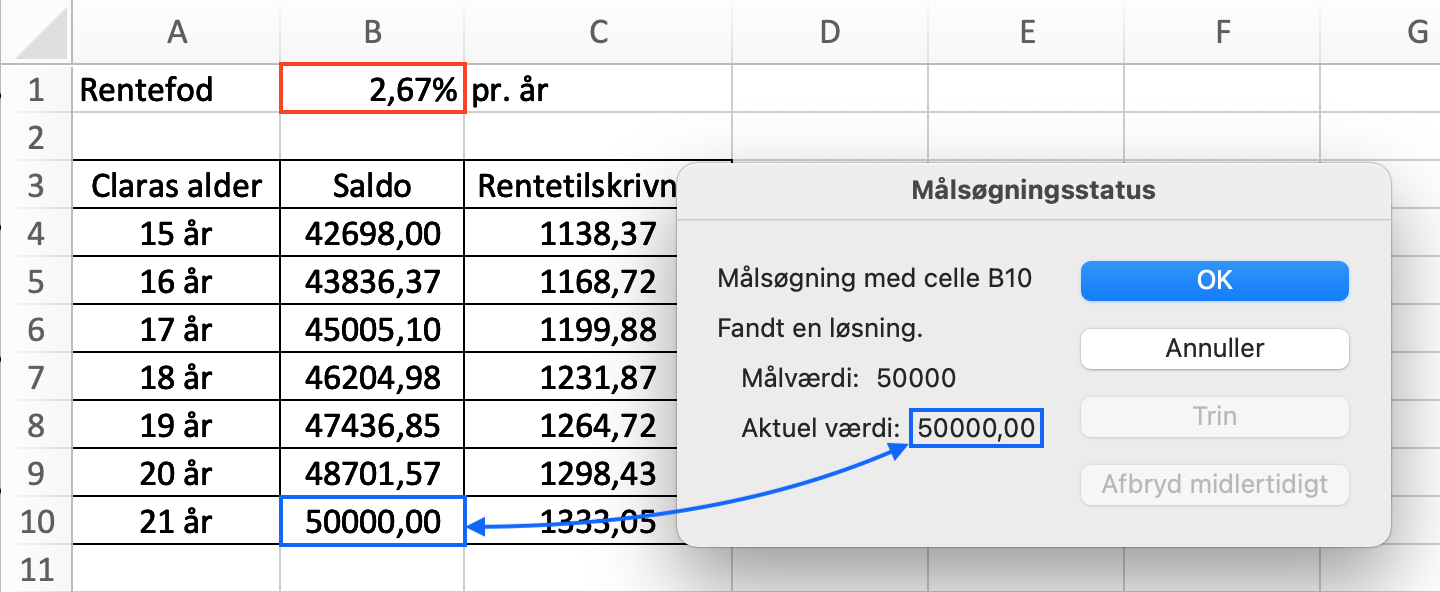
  5. Man bruger Funktioner - Målsøgning i Excel til at løse opgaven. Man får nedenstående resultat. Det vil sige, at rentefoden skal være 2,67 %, hvis der skal stå 50.000 kr. på Claras opsparingskonto, når hun fylder 21 år.

Svar på opgave 5: Hvor langt er der til øen?

  1. Tegning med rigtige målforhold tegnet i Geogebra:
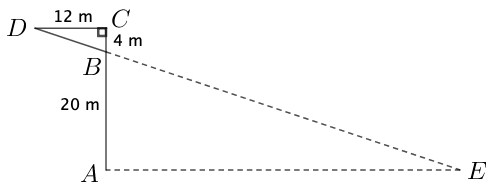
  2. De to trekanter er ligedannede fordi, de er ensvinklede. Det sidste følger af at de har en ret vinkel hver. Desuden er ∠CBD = ∠ABD, fordi de er topvinkler. Endelig er de to sidste vinkler ens, hvilket følger af reglen om, at summen af vinkler i en trekant er 180 °.
  3. Skalarfaktoren mellem de to ligedannede trekanter ABE og BCD er 12/4 = 5. Man skal finde |AE| i trekanten ABE. Den ensliggende side til AE i trekant BCD er siden CD, som har længden 12. Dette skal ganges med skalarfaktoren for at finde |AE|, dvs: |AE| = 5·12 m = 60 m
  4. Man måler ∠B og finder |AE| ud fra formlen: tan(∠B) = |AE|/(20 m) ⇒ |AE| = (20 m)·tan(∠B)

Svar på opgave 6: Figurfølge

  1. Arealet af en dragefirkant er 0,5 gange produktet af diagonalernes længder, dvs arealet af figur 2 = 0,5·4·6 = 12
  2. Arealet af figur 4 = 0,5·8·12 = 48
  3. Ved at prøve sig frem finder man at figur 5 har arealet 0,5·10·15 = 75 og figur 6 har arealet 0,5·12·18 = 108. Da 99 ligger mellem 75 og 108 er der ikke nogen figur, der har arealet 99
  4. Figur n i følgen har arealet: 3·n2