Svar på opgave 1: Simons fritidsjob

1. Simon tjener 32 timer · 55,35 kr./time = 1.771,20 kr.
2. Simon skal arbejde (24.000 kr.)/(55,35 kr./time) = 433,6 timer
3. Simon får i gennemsnit udbetalt pr. måned: [24.000 kr./12] - [24.000 kr./12]·8% = [2.000 kr.] - [2.000 kr.]·0,08 = 2.000 kr. - 2.000 kr.·0,08 = 2.000 kr. - 160 kr. = 1.840 kr.
4. Hans årsløn kaldes x. Der gælder, at
   x - x·0,08 - x·0,044 = 32.200 kr. ⇔
   x·(1 - 0,08 - 0,044) = 32.200 kr. ⇔
   x·0,876 = 32.200 kr. ⇔
   x = 32.200 kr./0,876 = 36.758 kr.
   Det vil sige, at Simons årsløn skal være 36.758 kr. for, at han får udbetalt 32.200 kr.

Svar på opgave 2: Simons opsparing

1. Simon mangler 13.500 kr. - 2.400 kr. = 11.100 kr. for at have råd til et kørekort.
2. Løsning i Excel:
   
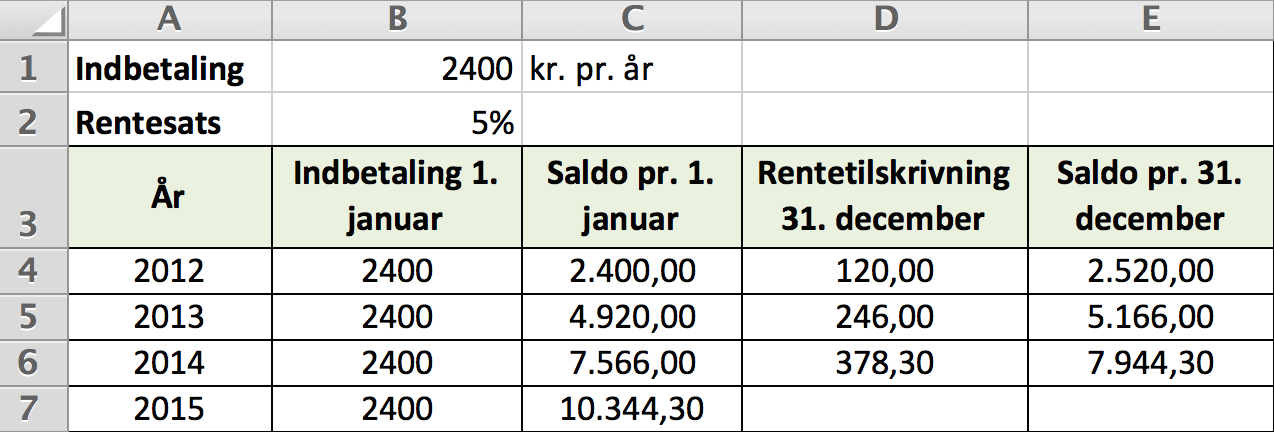
3. Løsning med målsøgning i Excel for et slutbeløb på 13.000 kr.
   Først vælger man feltet saldoen for 1. januar. Det er C7. Dernæst vælger man feltet med det faste beløb. Det er B4. (Der står $ udfor bogstav og tal i feltet, fordi feltet holdes fast.) Man sætter grænsen for saldoen til 13000.
   
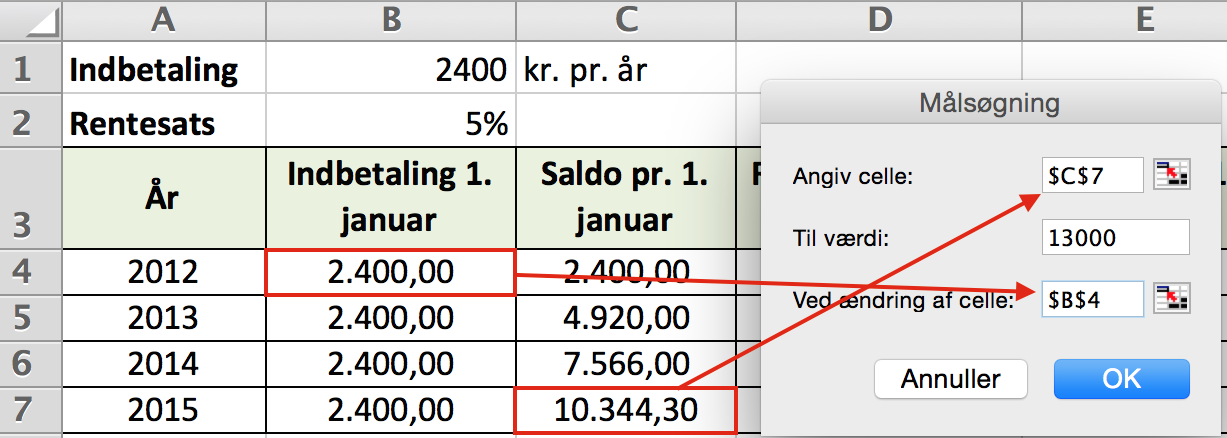
   Derefter trykkes OK og man får resultatet:
   
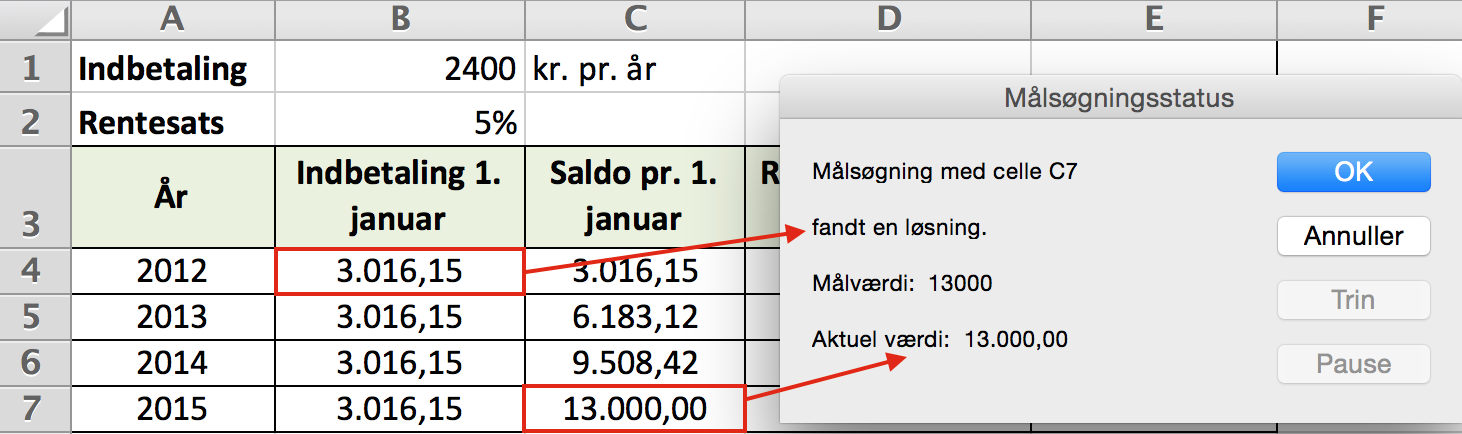
   Heraf ses at det indsatte beløb skal være 3.016 kr. om året, når prisen på et kørekort er 13.000 kr.
   Tilsvarende får man det indsatte beløb til 3.248 kr. hvis prisen for et kørekort er 14.000 kr.
4. Simons opsparing følger kurven m der hele tiden vokser hurtigere med renters rente eller eksponentielt.
   Kurven n vokser lineært og kurven l vokser først hurtigere og hurtigerer for derefter at vokse langsommere og langsommere.

Svar på opgave 3: Højden af en silo

1. Simon går 50 m/(0,85 m/skridt) = 50/0,85 skridt = 58,8 skridt
2. De to trekanter er ligedannede fordi, de har de samme vinkler. Det følger af, at de har vinklen A til fælles og af, at A's modstående sider er parallelle for de to trekanter. Dermed er alle sider i de to trekanter parvist parallelle og vinklerne defor ens.
3. Siloens højde er 150 cm + |BC|. Skaleringsfaktoren mellem trekant ABC og trekant ADE er: |AC|/|AE| = (50 m)/(60 cm) = (50 m)/(0,6 m) = 83,3. Dermed er: |BC| = 0,3 m·83,3 = 25 m.
   Dvs. siloens højde er: 1,50 m + 25 m = 26,5 m
4. Man skal finde |AD|. Man bruger Pythagoras læresætning og får:
   (60 cm)² + (30 cm)² = |AD|² ⇔
   |AD|² = 3.600 cm² + 900 cm² ⇔
   |AD|² = 4.500 cm² ⇒
   |AD| = √[4.500] cm ⇔
   |AD| = 67,1 cm.
   Det vil sige, at der er 67,1 cm fra Julies øje til pindens overkant
5. Símon har ret, idet tangens til en spids vinkel i en retvinklet trekant er lig med den modstående katete til vinklen divideret med den hosliggende katete til vinklen.

Svar på opgave 4: Simons kondital

1. Simons maksimale puls er 208 - 0,7·15 = 197,5
2. Alderen sættes til x. Der gælder:
   194 = 208 - 0,7·x ⇔
   x = (208 - 194)/0,7 ⇔
   x = 20
   Det vil sige, at 194 i makspuls svarer til en alder på 20 år
3. Man skal finde VO₂max af formlen og omregne det til konditallet.
   VO₂max = (262/0,23)·(60/21.100) + 0,25 L/min. = 3,489 L/min.
   Heraf fås, at konditallet er lig med: 3,489·1000/64 = 54,5
4. a) og d) er forkerte. Fejlen ved a) er, at 0,25 er sat ind i en parentes, hvor det ikke hører hjemme. I d) er 0,25 sat ind på en brøkstreg, hvor det ikke hører hjemme.

Svar på opgave 5: Fravær i Simons klasse

1. Hyppighedstabel for fravær i 9. A
   

   Antal fraværsdage i 9. A	Hyppighed (antal elever)
   0	6
   1	5
   2	5
   3	3
   4	2
   5	1
   6	1
   7	1

2. Der er 24 elever i 9. A. Otte af dem var fraværende i mere end 2 dage.
   Dette giver at 8/24 = 33 % var fraværende i mere end 2 dage.
   Tabellen nedenunder viser med rødt de elever, der var fraværende i mere end 2 dage.
   

   Antal fraværsdage i 9. A	Hyppighed
   0	6
   1	5
   2	5
   3	3
   4	2
   5	1
   6	1
   7	1

3. Man finder antallet af elever i 9. B ved at lægge hyppighederne sammen.
   Det giver: 0 + 2 + 5 + 5 + 2 + 0 + 2 + 3 = 19 elever
4. Nedenstående figur er et søjlediagram for fraværet i 9. B.
   
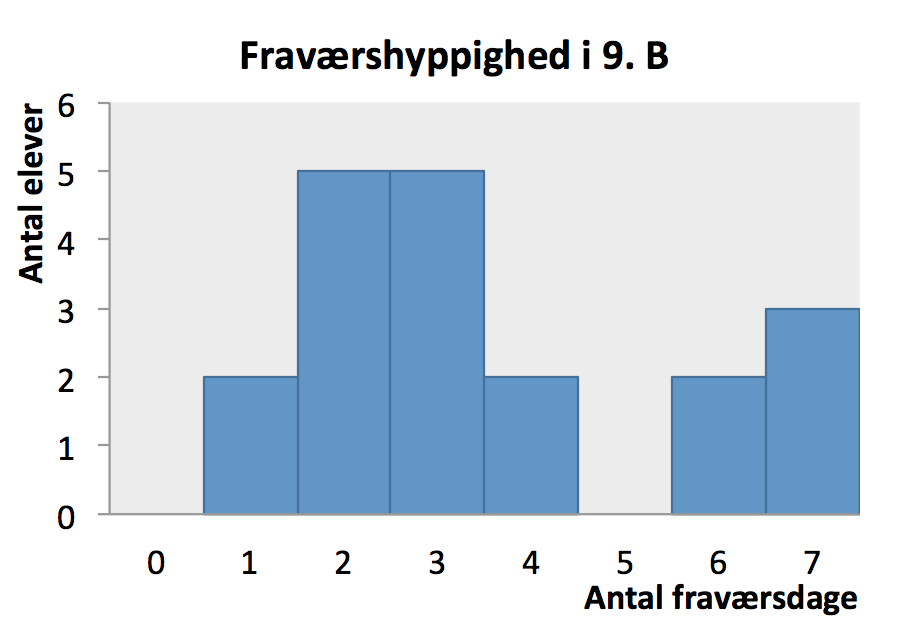
5. Nedenunder er vist et boksplot for fraværet i henholdsvis 9 A. og 9. B.
   
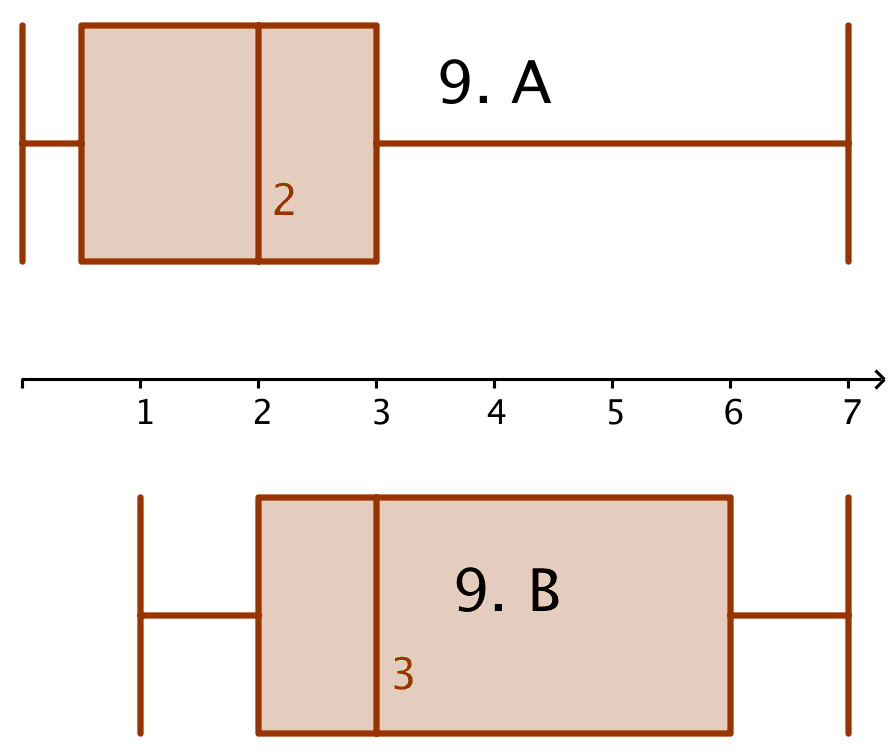
   Det ses at 9. A har lavere gennemsnit (median) end 9. B. Medianen for 9. A er 2, mens den for 9. B er 3.
   Desuden ligger 9. A hyppigheder er tættere samlet end 9. B. Hos 9. A er der enkelte, der har et højere fravær end flertallet, mens fraværet for 9. B er mere jævnt fordelt blandt eleverne.
   Kvartilsættet for 9. A er som det ses 25%-faktil: 0,5; median: 2; 75 %-fraktil: 3.
   Kvartilsættet for 9. A er som det ses 25%-faktil: 2; median: 3; 75 %-fraktil: 6.

Svar på opgave 6: En figur af kvarte cirkler

1. For at en firkant skal være et kvadrat skal alle sider være lige lange, og alle vinkler skal være 90°
2. Figuren tegnet i Geogebra
   
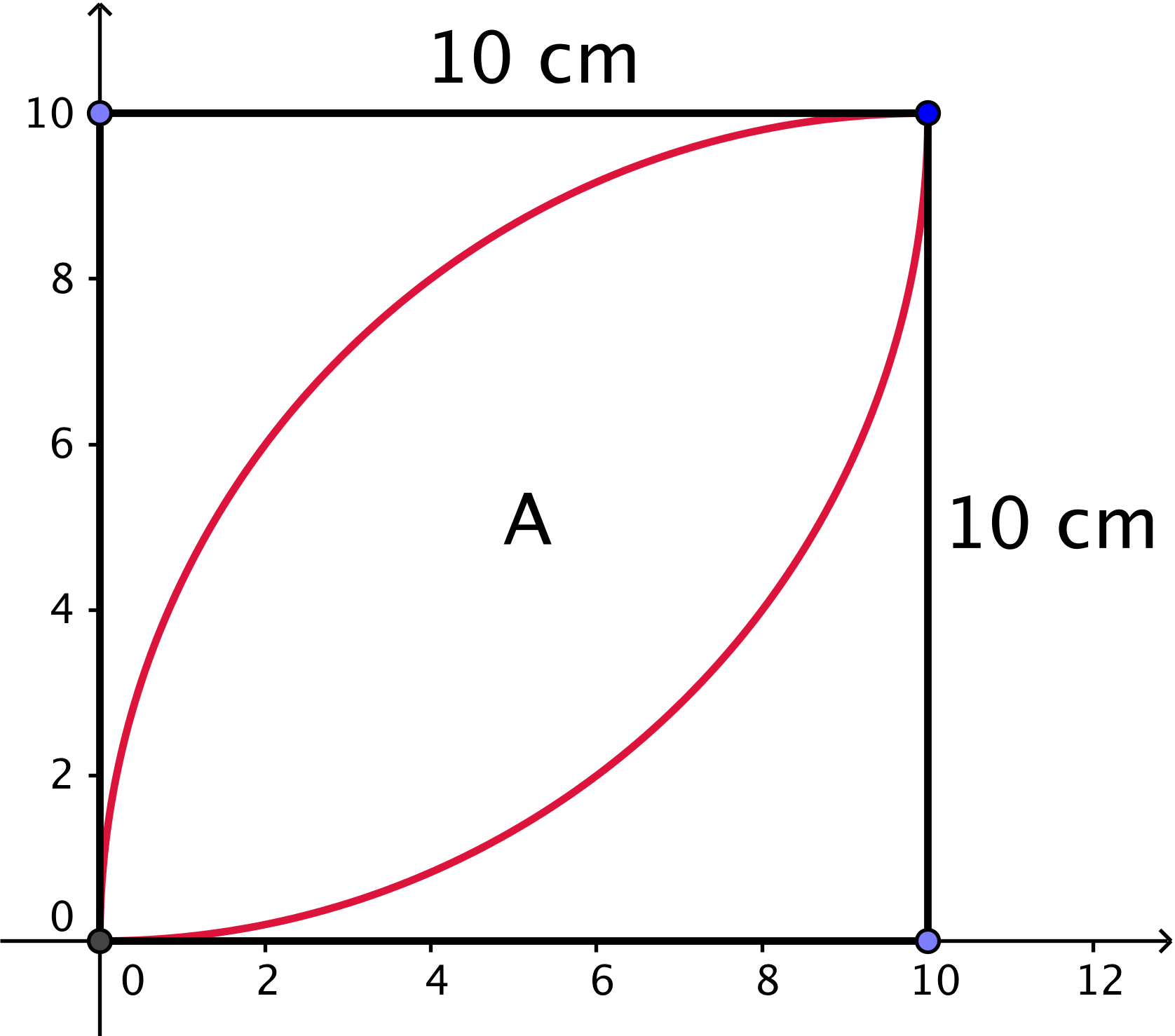
3. Omkredsen af kvadratet er 4·10 cm = 40 cm og arealet er (10 cm)² = 100 cm²
4. Omkredsen af figuren A er 2 gange buen af en kvartcirkel med radius 10 cm. Omkredsen er 2·[(1/4)·2·π·10 cm] = 10 π cm = 31,4 cm
5. Ved at fjerne A fra den ene kvartcirkel kan den ene kvartcirkel og resten af den anden lægges sammen til kvadratet. Det vil sige, at arealet af A er arealerne af de to kvartcirkler minus arealet af kvadratet som vist nedenunder.
   
   Arealet af en af kvartcirklerne er (1/4)·π·(10 cm)² = 100·π cm².
   Arealet af A bliver derfor: 2·(1/4)·π·(10 cm)² cm² - 100 cm² = ((1/2)·π·100 - 100) cm² = 57,1.