Svar på opgave 1: Region Nordjylland

1. Danmarks samlede befolkningstal er: (0,6 + 1,2 + 1,2 + 0,8 + 1,6) mio. indbyggere = 5,4 mio. indbyggere.
2. I region Nordjylland bor der 0,6 mio. indbyggere. Deres andel af den samlede befolkning er
   (0,6/5,4)·100 % = 11,1 %
3. (0,6 mio. indb.)/(8000 km²) = (600.000 indb.)/(8000 km²) = 75 indb./km²
   (5,4 mio. indb.)/(43000 km²) = (5.400.000 indb.)/(43.000 km²) = 126 indb./km²
4. Nedenunder er indbyggertal og indbyggertæthed indrammet med rødt for Mariagerfjord og Morsø.
   
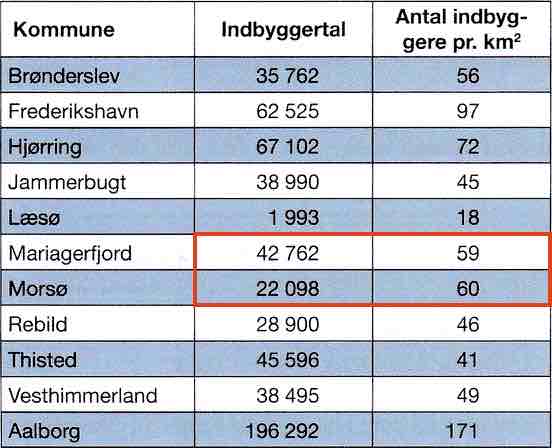
   Arealet af regionerne beregnes som indbyggertal/(indbyggere pr. km²). Man får:
   Areal af Mariagerfjord kommune: (42.762 indb.)/(59 indb./km²) = 42.762/59 km² = 724,8 km²
   Areal af Morsø kommune: (22.098 indb.)/(60 indb./km²) = 22.098/60 km² = 368,3 km²
   Dette viser, at Mariagerfjord komunne er større end Morsø kommune.
5. Nedenfor er vist et søjlediagram lavet i Excel over kommunernes indbyggertal.
   
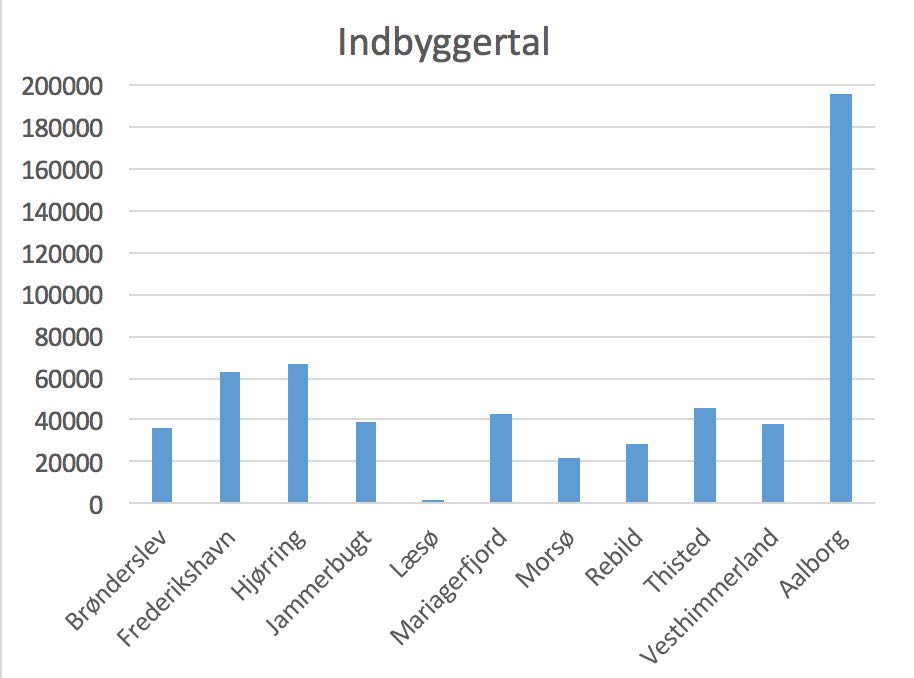
6. Det gennemsnitlige indbyggertal er (35.762 + 62.525 + 67.102 + 38.990 + 1.993 + 42.762 + 22.098 + 28.900 + 45.596 + 38.495 + 196.292)/11 = 52.774.
   Det ses af tabellen, at følgende tre kommuner ligger over gennemsnittet:
   Frederikshavn (62.525 indb.), Hjørring (67.102 indb.) og Aalborg (196.292 indb.).

Svar på opgave 2: Fra Holbæk til Skagen

1. Den længste rute er 476 km og den korteste er 346 km. Forskellen er (476 km - 346 km) = 130 km
2. Den samlede rejselængde fra Holbæk til Skagen via Kalundborg-Århus ruten er 367 km, som det fremgår af kortene. Sejllængden er 89 km, som det fremgår af skemaet.
   Det vil sige, at den samlede rejselængde i bil er 367 km - 89 km = 278 km
3. Den samlede rejsetid via Kalundborg-Århus er 5 timer og 42 min. Sejltiden er 2 timer og 40 min. Forskellen er:
   5 timer + 42 min. - (2 timer + 40 min.) =
   5 timer - 2 timer + (42 min. - 40 min.) =
   3 timer og 2 min.
4. Rejselængden er 476 km. Med en rejsetid på 5 timer og 9 min. bliver gennemsnitshastigheden:
   (476 km.)/(5 timer og 9 min.) =
   (476 km.)/(5 timer + (9/60 time)) =
   (476 km.)/(5,15 timer) = 92,4 km/t
5. Nedenunder er beregningen forklaret.
   
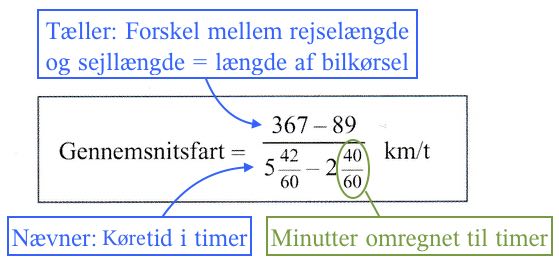
6. (367 - 89)/[(5 + 42/60) - (2 + 40/60)] km/t =
   278/[5,70 - 2,67] km/t =
   278/3,03 km/t =
   91,6 km/t
7. Nedenunder er skemaet udfyldt med mellemregninger.
   
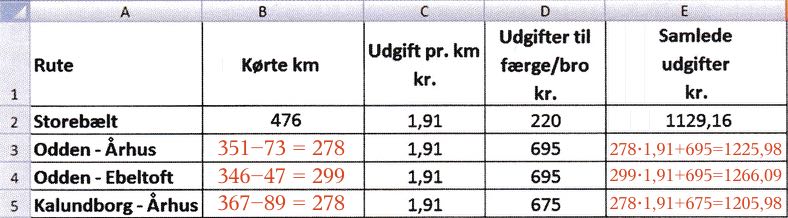
8. Nedenunder er skemaet udfyldt med prisen pr. km lig med 3,00 kr.
   
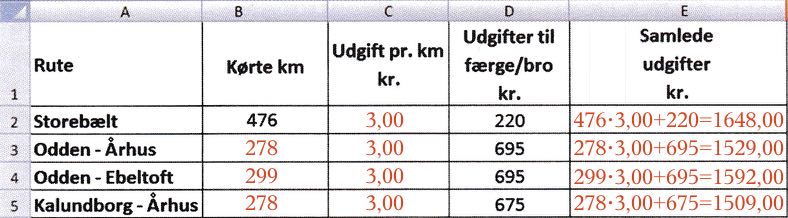
   Vejen over Kalundborg-Århus er den billigste (1509 kr.).
9. Prisen pr. kørt kilometer kaldes x.
   Den samlede pris for rejsen over Storebæltsbroen er (476·x + 220) kr.
   Den samlede pris for rejsen over Kalundborg-Århus er (278·x + 675) kr.
   Disse udtryk sættes lig med hinanden (uden enheder) for at finde x:
   476·x + 220 = 278·x + 675 ⇔
   x = (675 - 220)/(476 - 278) ⇔
   x = 2,298
   Det vil sige, at prisen skal være 2,30 kr. pr. kørt km for at turen via Storebæltsbroen skal være lige så dyr som turen via færgen Kalundborg-Århus.

Svar på opgave 3: Råbjerg mile

1. På nedenstående figur fra Geogebra er billedet tilpasset så målestokken har en længde af 500 i koordinatsystemet.
   (Tilpasningen foregår ved, at man måler længden af målestokken, a, og den vandrette længde af billedet, b, og ganger a/b med 500. Det tal, som man får, er x-værdien for nederste højre hjørne af billedet. Det er her 4774).
   
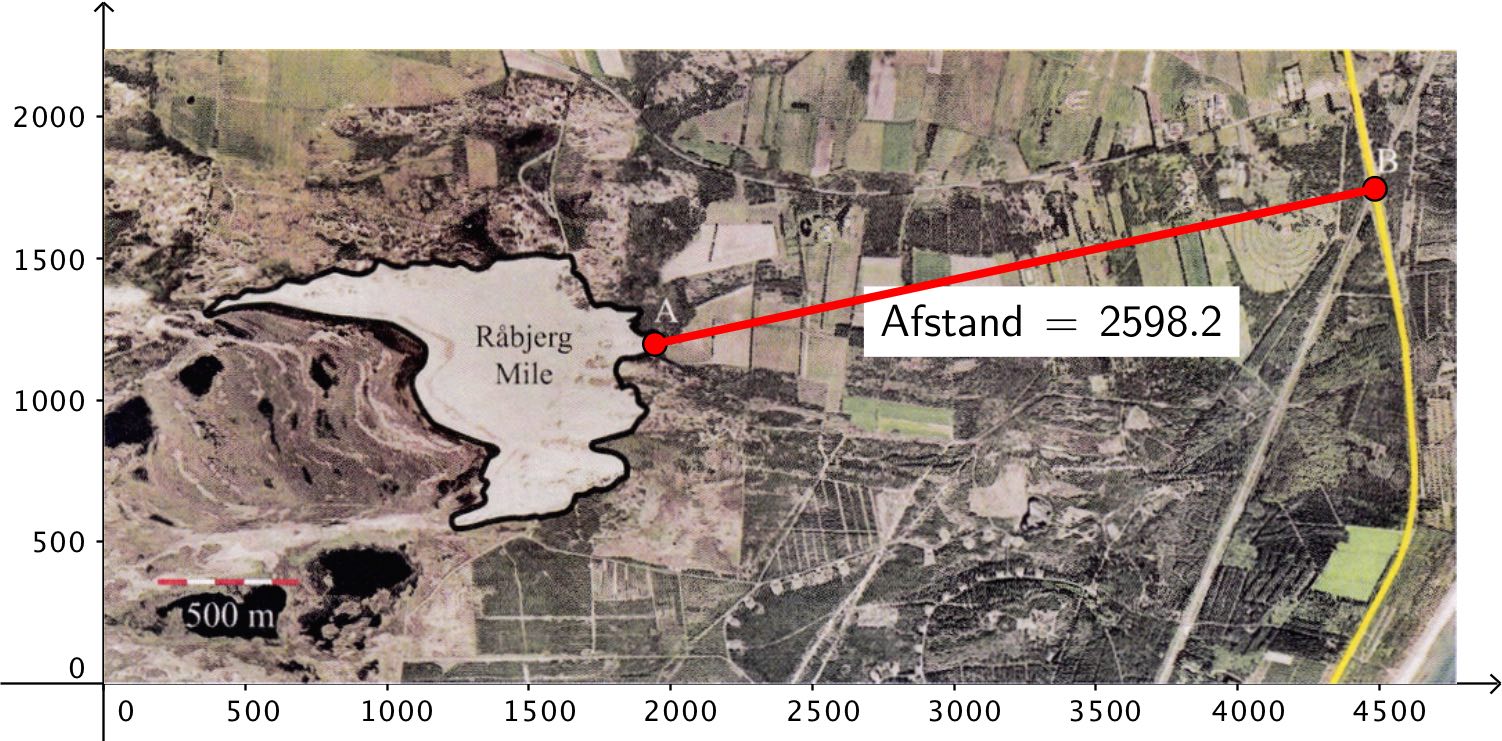
   Afstanden mellem A og B måles derefter som vist til ca. 2.600 m
2. Milen bevæger sig med en hastighed af 15 meter pr. år = 15 m/år. Hvis afstanden antages at være 2600 m, vil det tage (2600 m)/(15 m/år) = (2600/15) år = 173 år. Idet man går ud fra at det nuværende år er 2010 vil milen nå punkt B i år...
   2010 + 173 = 2183
3. Nedenfor er vist et udsnit af billedet fra opgaven med målestokken og en tern.
   
   Det viser, at en tern er 500 m på hver led. Dermed er arealet af en tern = (500 m)² = (0,5 km)² = 0,5² km² = 0,25 km²
4. Råbjerg mile kan på øjemål ligge inden for det blå rektangel, der er vist på billedet nedenunder.
   
   Rektanglet har som vist dimensionerne længde = 1000 m = 1 km og bredde = 700 m = 0,7 km. Dermed bliver arealet af Råbjerg mile: (0,7 km)·(1 km) = 0,7 km²
5. Nedenunder er grafen for højden af Råbjerg mile vist. X-aksen er trukket op med en rød stiplet linje, der svarer den røde stiplede linje på kortet.
   
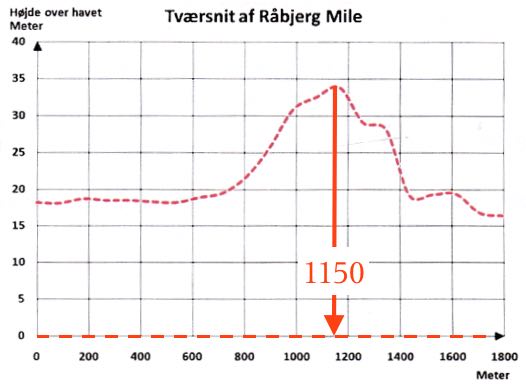
   Det ses at højeste punkt findes ca. 1150 m fra punktet 0, der må anses for at svare til venstre ende af den røde stiplede linje på kortet. Punktet for største højde af milen er tegnet ind på kortet nedenunder.
   

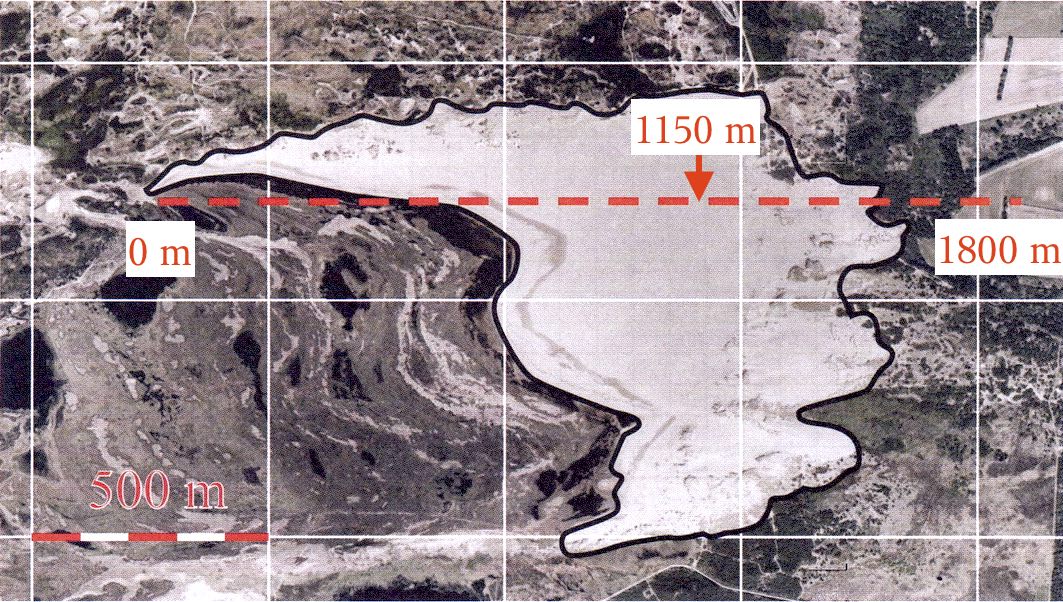
Svar på opgave 4: Salt på Læsø

1. Laget findes i ca. 2 meters dybde som vist nedenunder.
   
2. Saltholdigheden er 14 %, dvs. 14 af vægten af saltvand er salt. Et ton salt indeholder dermed (1 t)·(14 %) salt = 140 kg salt
3. Sammenhængen er y = 0,14x, hvor y er saltet vægt i saltvandet og x er vægten af saltvand.
   Som graf er det en ret inje med hældningen 0,14 gennem (0,0).
4. Et æg med rumfanget 60 mL og massen 65 g har en massefylde på (65 g)/(60 mL) = 1,083 g/mL eller 1,083 g/cm³
5. Nedenunder er punktet afmærket på grafen med en rød prik, der er ud for tallet 1,08 på y-aksen.
   
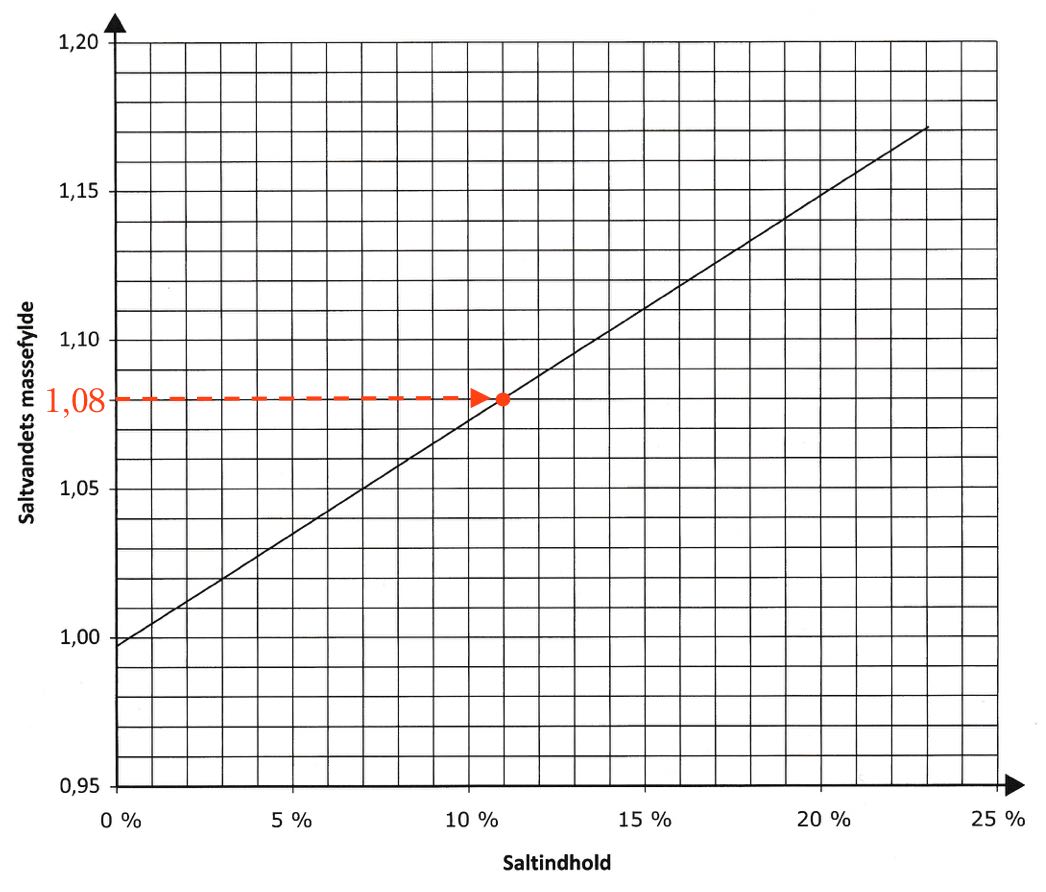
6. Nedenunder er saltholdigheden der svarer til massefylden 1,08 aflæst til 11 %
   

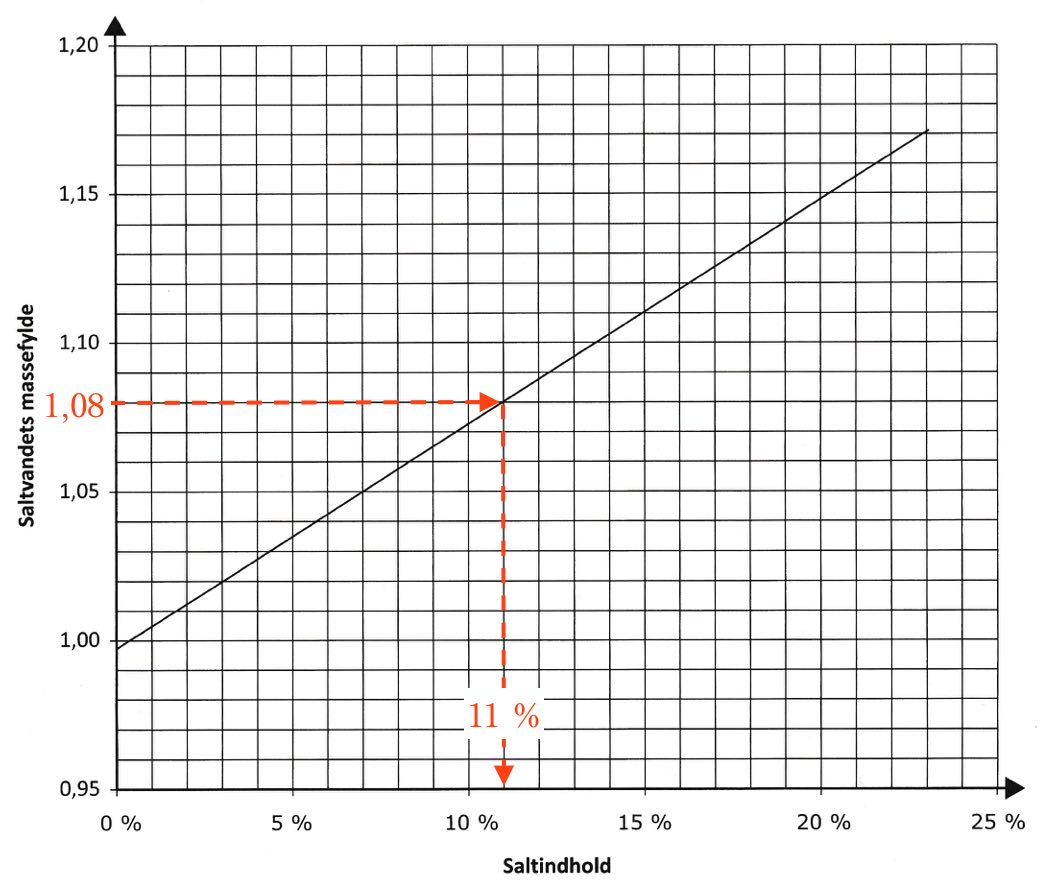
Svar på opgave 5: To kvadrater og en cirkel

1. Nedenunder er figurene tegnet i Geogebra. Først tegnes det blå kvadrat og dernæst dets diagonaler. Skæringspunktet mellem diagonalerne kaldes A. Dette er cirklens centrum. Man halverer den ene side i det blå kvadrat. Dette er punktet B. Afstanden |AB| er cirklens radius.
   Skæringspunkterne mellem det store kvadrats diagonaler og cirklen er hjørnerne i det indskrevne (røde) kvadrat. Et af skæringspunkter er vist som punktet C.
   
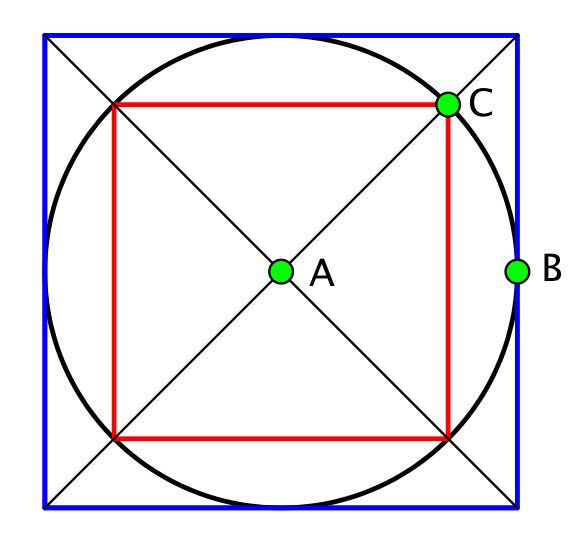
2. Cirklens diameter er lig med siden i det omskrevne kvadrat. Dets areal er derfor (10 cm)² = 100 cm²
3. Cirklens diameter er lig med det omskrevne kvadrats side og det indskrevne kvadrats diagonal. Siden i et kvadrat er lig med dets diagonal divideret med kvadratrod 2 (det følger af Pythagoras læresætning).
   
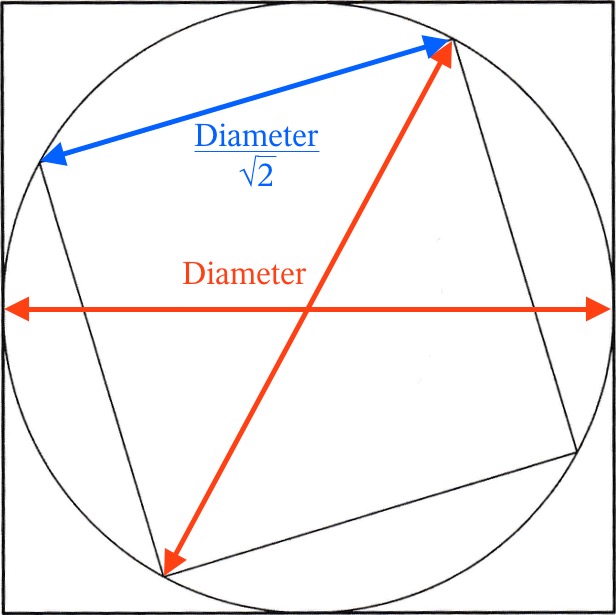
   Kalder man diagonalen for d gælder derfor, at arealet af det omskrevne kvadrat = d² og det indskrevne kvadrats areal = (d/√2)² = d²/2.
   Forholdet (areal af stort kvadrat)/(areal af lille kvadrat) = d²/(d²/2) = 2.
   Det vil sige, at det omskrevne kvadrat er dobbelt så stort som det indskrevne kvadrat.