Svar på opgave 1: Besøg i Eiffeltårnet
- I september er elevatoren åben i tidsrummet: 9.30 - 23.45
- Der er 23 - 9 timer = 14 timer fra 9.30 til 23.30. Fra 23.30 til 23.45 er der 15 minutter. I alt er elevatoren åben i 14 timer og 15 minutter
- Klassen er på 22 elever og kan derfor få rabat. Begge lærere kommer gratis ind, da der er 20 elever eller mere. Prisen for hele klassen bliver: 22·8,30 € = 182,60 €
-
Den normale pris uden rabat i € er: 22·9,90 € + 2·13,00 € = 243,80 €
Kursen på € er 744, det vil sige, at 100 € = 744 DKK
Pris for tilbud i DKK: (182,60 €)·(744 kr./100 €) = 1358,54 DKK
Normalpris i DKK: (243,80 €)·(744 DKK/100 €) = 1813,87 DKK
Forskellen mellem de to beløb er: 1813,87 DKK - 1358,54 DKK = 455,33 DKK - I 1889 var der 1,95 mio. besøgende. I 1989 var der 5,6 mio. besøgende. Forskellen er: (5,6 - 1,95) mio. = 3,65 mio besøgende
-
Man skal finde ud af, hvor stor en procentdel, som den røde del af cirkeldiagrammet udgør af hele cirklen. Cirkeludsnittes vinkel er 205°. Dets andel af cirklen er: 205°/360° = 0,569 = 57%
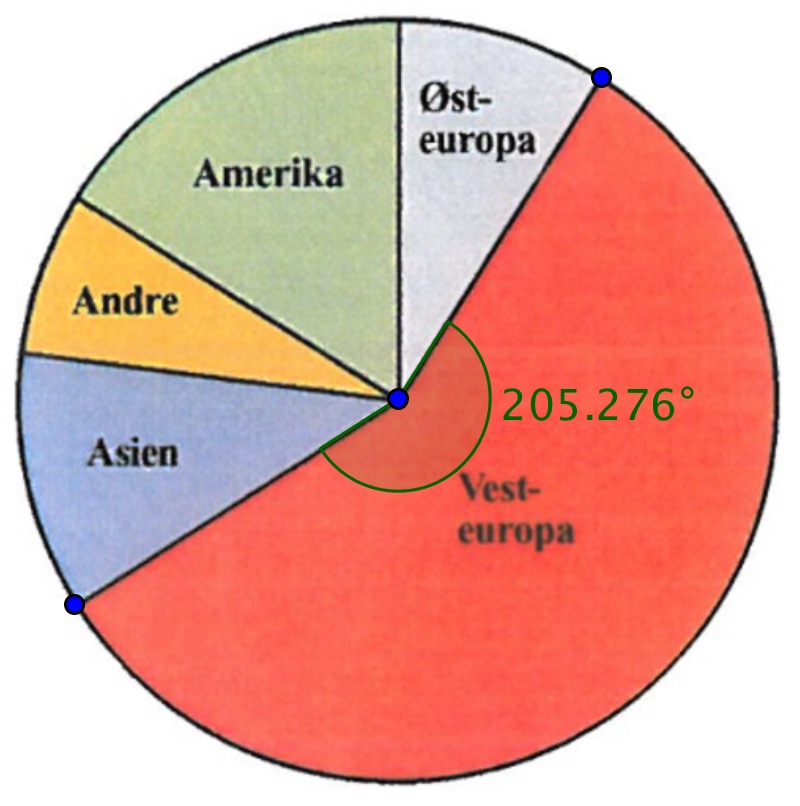
- Danskerne udgør 1% af de besøgende, der kommer fra vesteuropa. Antallet af danskere er derfor 1% af 57% af 6.428.441. Det vil sige, at antallet af danskere er 0,01·0,57·6.428.442 = 36.642
Svar på opgave 2: Bygningen af Den Kinesiske Mur
- Man begyndte at bygge muren 220 år f.kr. det vil sige i år -220. I 2010 var det 2010 - (-220) = 2230 år siden
- Samlet antal mennesker: 300.000 + 300.000 + 1.800.000 = 2,4 mio.
- Trapezens areal er (1/2)·7·(4,5 + 6,0) m2 = 36,75 m2
- Massen er rumfanget af sten gange stenenes massefylde. Rumfanget er længde af stenfyld gange tværsnitsareal af stenfyld. Det vil sige, at massen er 36,75 m2·2 m·1,5 ton/m3 = 110,25 ton
-
Tabel over fyldets masse som funktion af murens længde.
Murens længde i meter 2 4 6 8 10 Fyldets masse i tons 110 220 330 440 550 -
Tegning i Geogebra:
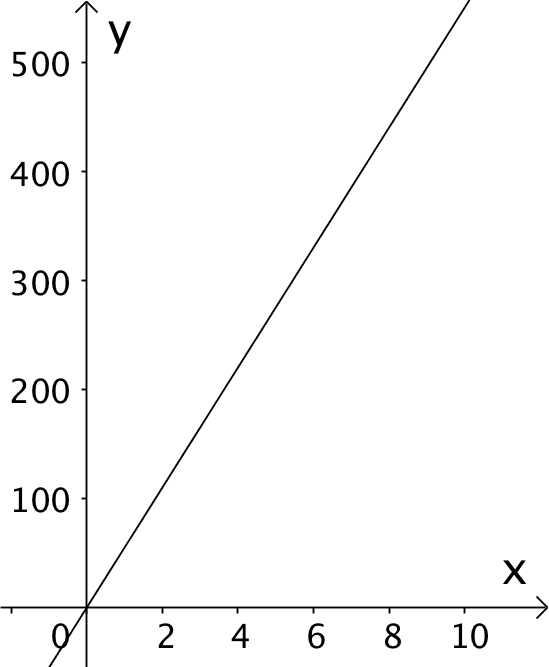
-
Forskriften er y = 55·x, hvor x er murens længde i meter, og y er fyldets masse i tons.
Det er forskriften for en ret linje gennem (0,0) med hældningen 55 (evt. 55 tons/m). Hældningen er 55 tons/m, fordi massen øges med 110 tons hver gang, man øger længden af muren med 2 m.
Svar på opgave 3: Panamakanalen - en genvej
- Forskellen er: 36.400 km - 11.200 km = 25.200 km
-
Sejltid:
Fra 18.35 til 19.00 = 25 min.
Fra 19.00 til 24.00 = 5 timer
Fra 00.00 til 01.13 = 1 time og 13 min.
I alt: 6 time og 38 min.
Gennemsnitsfart: (81 km)/(6 timer + 38 min.) = (81 km)/[(6 + 38/60) t] = (81 km)/(6,633 t) = 12 km/t - Normal gennemsnitsfart: (20 knob)·1,852 [(km/t)/knob] = 37,04 km/t = 37,0 km/t
- Sejltiden rundt om Sydamerika er (36.400 km)/(37,04 km/t) = 983,78 timer = (983,78 timer)/(24 timer/1 døgn) = 41 døgn Forskel i sejltid = 41 døgn - 13 døgn = 28 døgn
Svar på opgave 4: Solstråler i Pantheon
-
Følgende tegning er lavet i Geogebra:
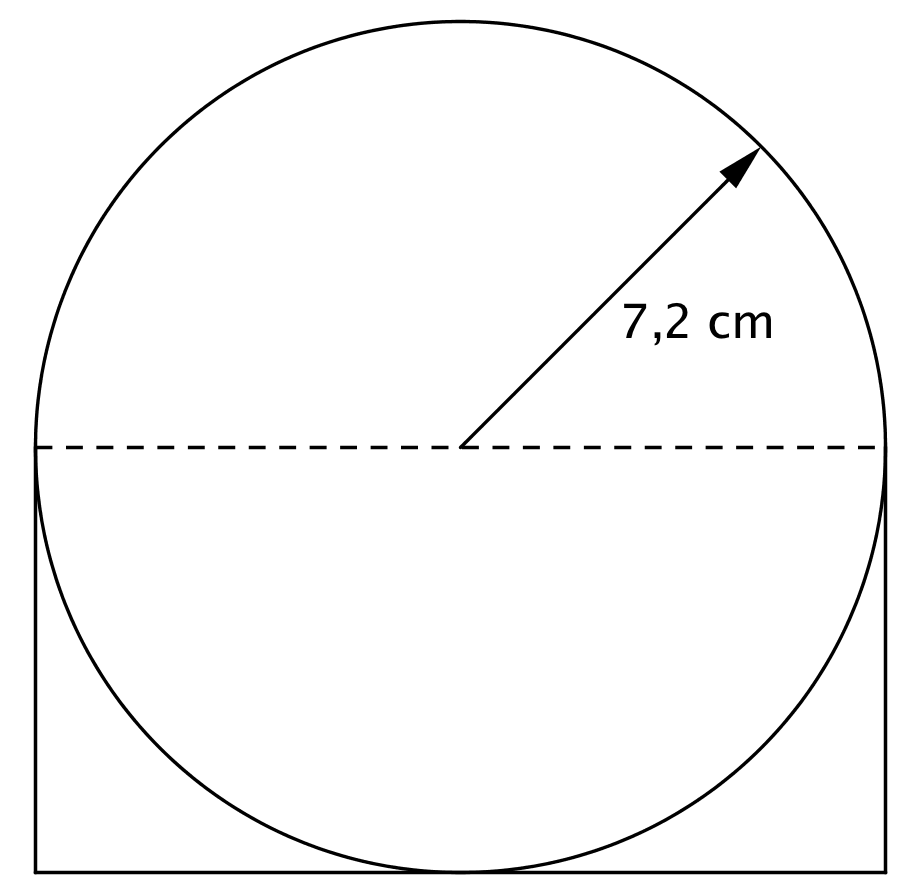
-
Tegnet i Geogebra:

-
Tegnet og målt nedenunder i Geogebra. Oculus måles på tegningen til 2,994 cm, som svarer til 300·2,99 cm = 897 cm = 8,97 m
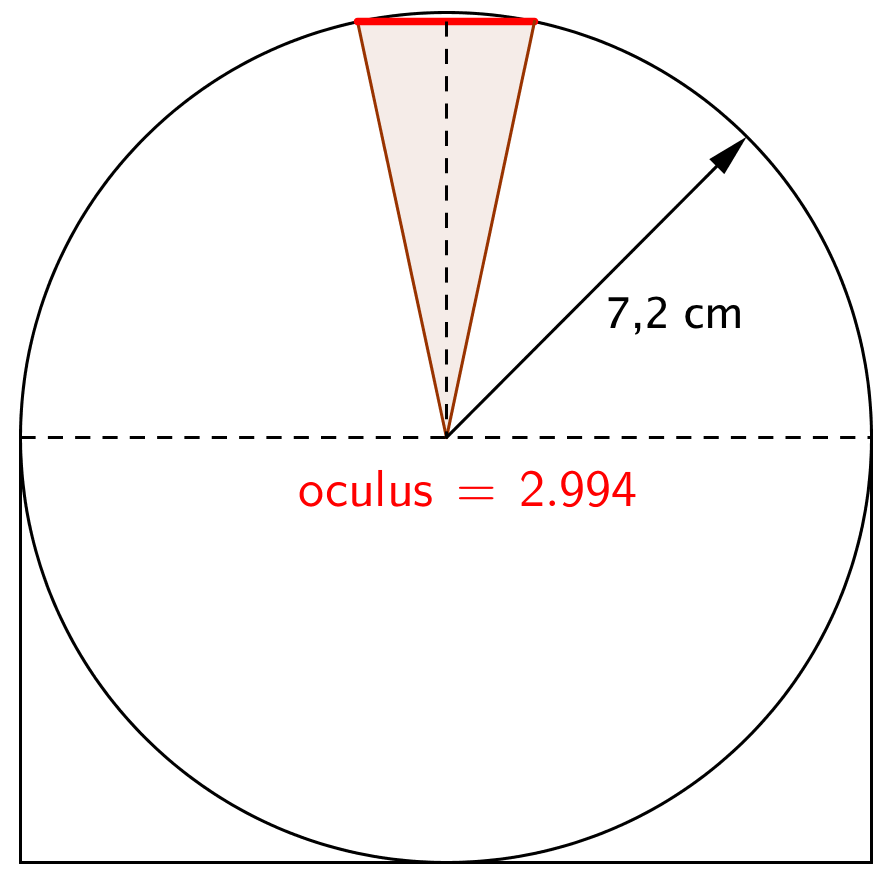
-
Løsningen nedenfor er tegnet og målt i Geogebra. Det ses, at sollyset vil ramme gulvet.
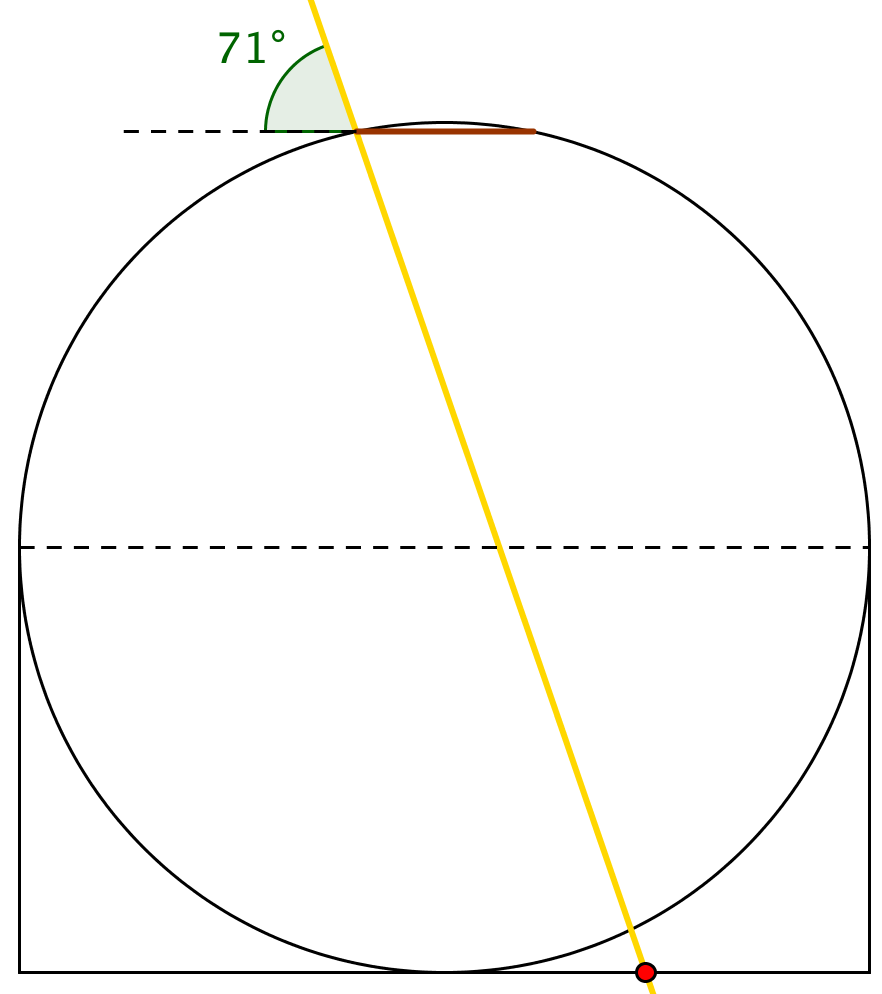
Svar på opgave 5: En trappepyramide i centicubes
- Der er 1 + 32 + 52 = 1 + 9 + 25 = 35
-
Sidelængden på et lag (antal centicubes langs med en side) vokser som 1, 3, 5, 7...osv. Antallet af centicubes i et lag er lig med sidelængden i anden.
Det vil sige, at i 4. lag er der 72 = 49 centicubes -
Tabel over lag nr. og antal centicuber i hvert lag.
Lag nr. 1 2 3 4 5 6 7 8 9 10 Antal 1 9 25 49 81 121 169 225 289 361 -
Pindediagram lavet i Geogebra ved at omsætte tabellens tal til punkter i et koordinatsystem og forbinde punkterne parvis lodret.
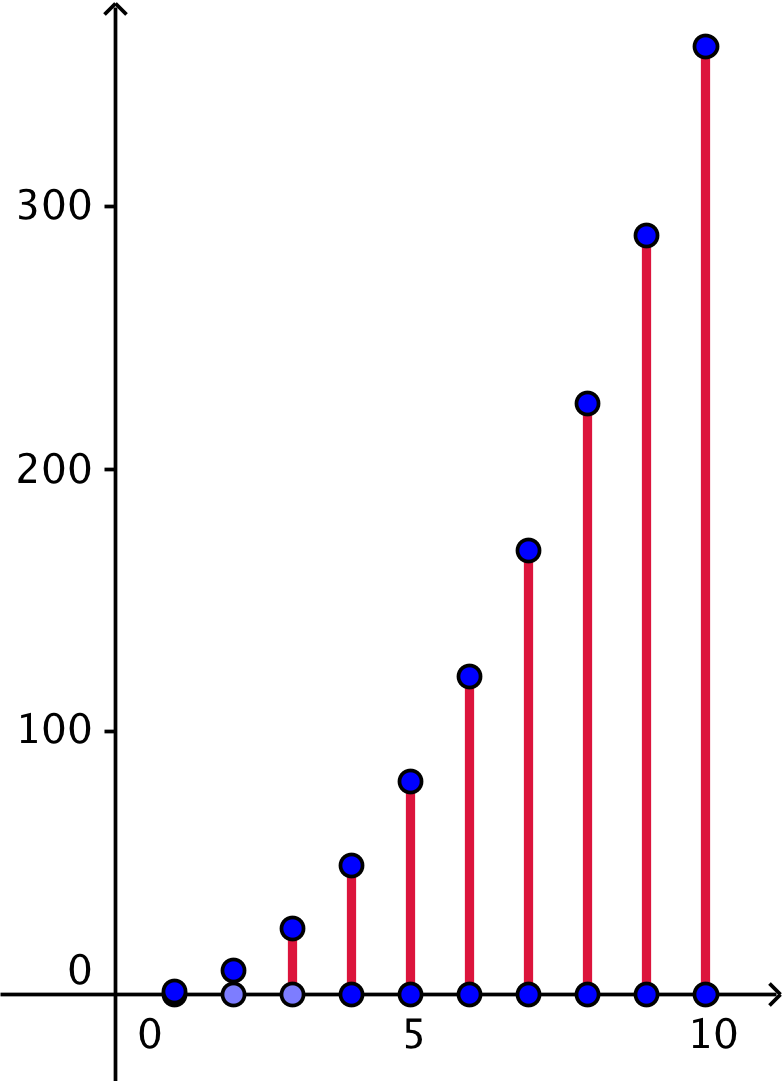
-
Lagnummeret kaldes n. Nedenfor er vist en tabel over antal centicuber i et lag for n = 1 til n = 4. Det ses, at der skal bruges (2·n - 1)2 centicuber i lag nummer n.
n antal centicuber i lag 1 1 = 12 = (n + 0)2 = (n + (n - 1))2 = (2·n - 1)2 2 9 = 32 = (n + 1)2 = (n + (n - 1))2 = (2·n - 1)2 3 25 = 52 = (n + 2)2 = (n + (n - 1))2 = (2·n - 1)2 4 49 = 72 = (n + 3)2 = (n + (n - 1))2 = (2·n - 1)2