Svar på opgave 1: Befolkningen i København 2007

1. Der boede 5.447.084 - 4.943.385 = 503.699 mennesker i København.
2. Følgende procentdel af den danske befolkning boede i København: (503.699/5.447.084)·100 % = 9,2 %
3. Befolkningstætheden er (antal mennesker i København)/(Københavns areal i km²) = (503.699 indb.)/(97 km²) ≈ 5200 indb./km²
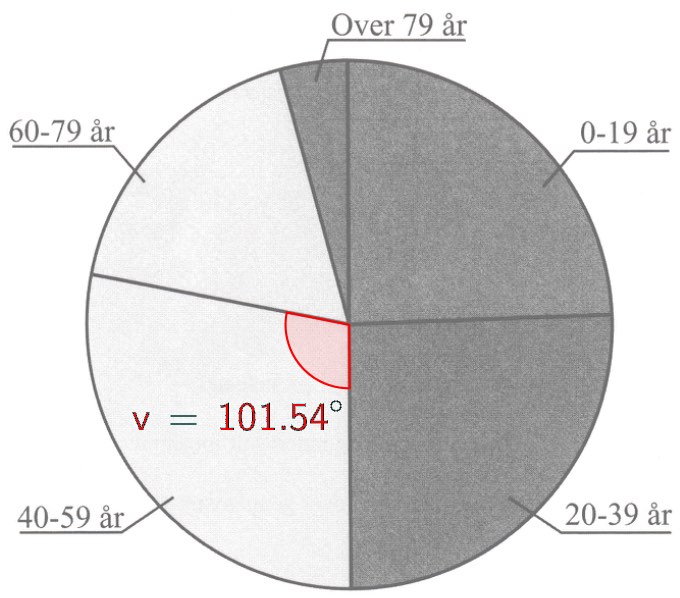
4. Man måler udsnittet vinkel i Geogebra til 101,54°. Denne vinkel udgør: (101,54°/360°)·100 % = 28,2 % af hele cirklen. Antallet af danskere mellem 40 og 59 år der dermed: (0,282)·(5.447.084) = 1.536.078
   
5. Nedenfor er skemaet fra opgaven udfyldt med andel og vinkel til diagrammet.
   
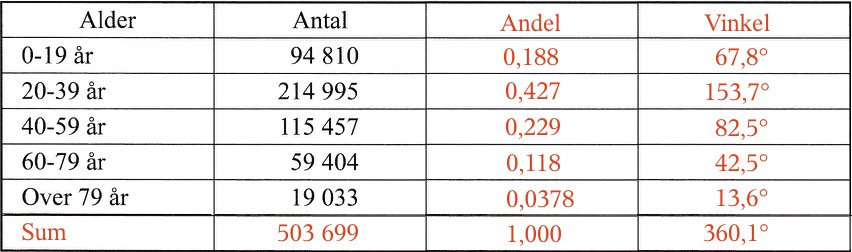
   Man starter med at summere antallet for hver aldersgruppe, og man dividerer derefter denne sum op i antallet for hver aldersgruppe for at finde andelen som denne aldergruppe udgør af den samlede befolkning.
   Til sidst beregnes vinklerne i diagrammet for hver aldersgruppe ved at gange hver andel med 360°.
   Ud fra skemaet tegnes følgende cirkeldiagram i Geogebra:
   
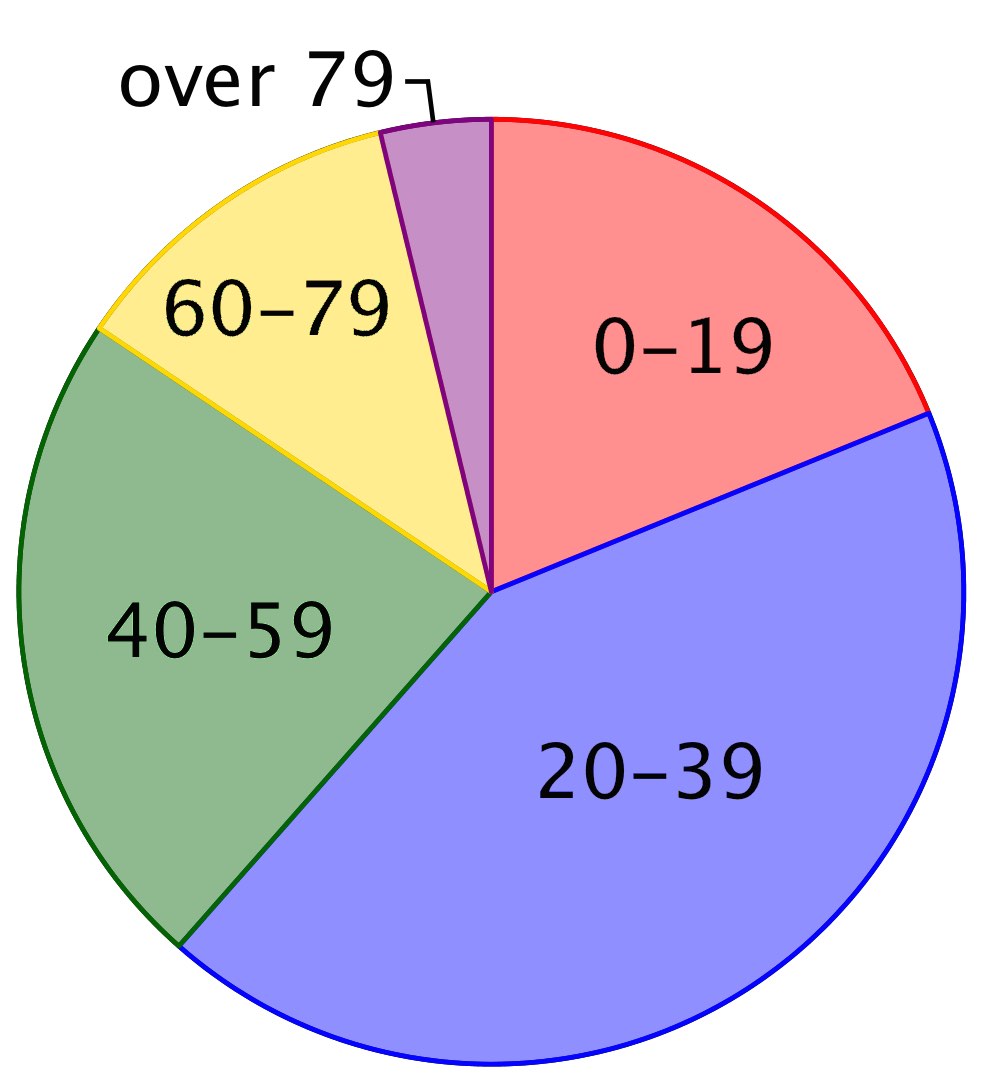
6. Man skal sammenligne cirkeldiagrammerne fra spørgsmål 4 og 5.
   Andelen af mennesker i aldersgruppen 20-39 er større for København end for resten af landet.
   Andelen af mennesker i aldersgruppen over 79 er nogenlunde den samme for København som for hele landet.
   Andelen af mennesker i hver af de andre aldersgrupper er mindre for København end for hele landet.

Svar på opgave 2: Københavns folketal i fremtiden

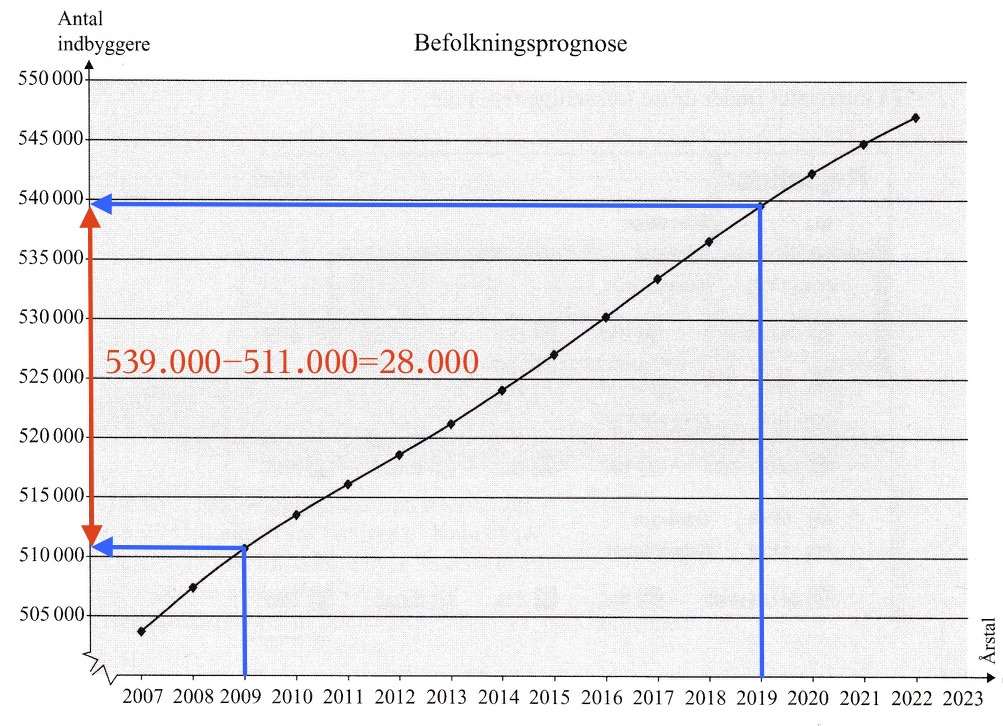
1. Befolkningtallet i 2019 aflæses som vist nedenunder til 539.000
   
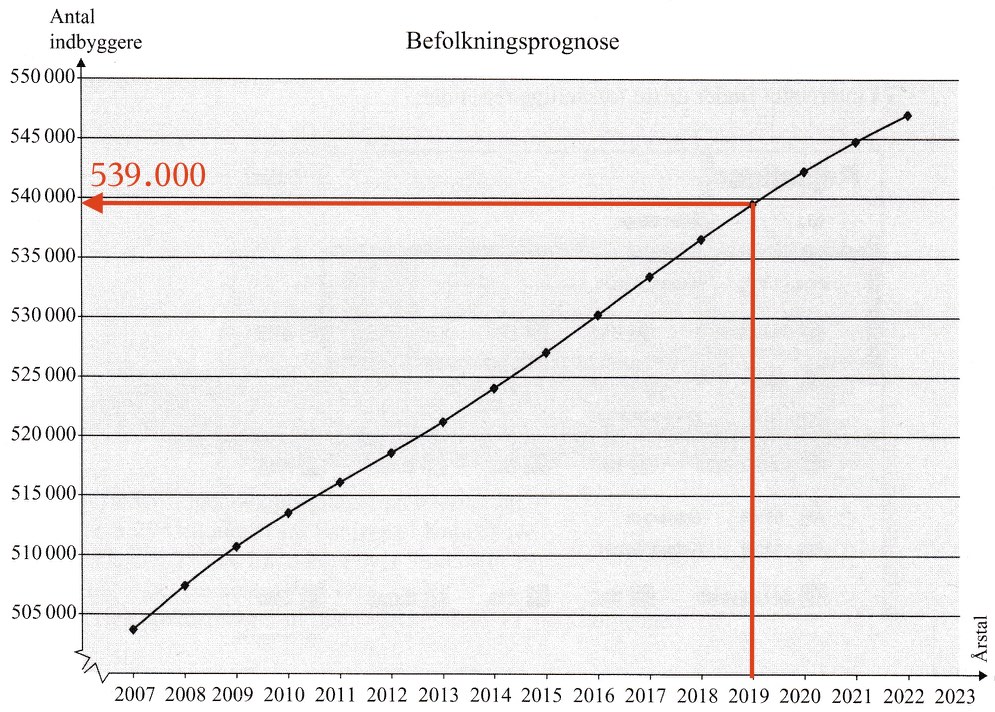
2. Befolkningtallet i 2009 og 2019 aflæses som vist nedenunder med blåt.
   Forskellen (vist med rødt) er 539.000-522.000 = 28.000
   
3. Man tager som eksempel x = 2010 (dvs. år 2010).
   Model 1 giver: y = 2.900·2010 - 5.316.000 = 513.000
   Model 2 giver: y = 2.900·2010 + 501.700 = 6.330.700
   Kurvens tal er ca. 513.000 der passer med model 1
4. I følge model 1 vil der i 2030 være: 2.900·2030 - 5.316.000 = 571.000 mennesker i Danmark i 2030.
5. For at finde året, x, hvor der er 600.000 mennesker i København, skal man løse følgende ligning:
   600.000 = 2.900·x - 5.316.000 ⇔
   x = (5.316.000 - 600.000)/2900 ⇔
   x = 2040
   Det vil sige, at Københavns befolkningstal passerer 600.000 i år 2040

Svar på opgave 3: Turen går til København

1. På den første rejseplan er rejsetiden:
   12:19 - 8:48 =
   12 timer + 19 min. - (8 timer + 48 min.) =
   4 timer - 29 min. =
   3 timer + 60 min. - 29 min. =
   3 timer og 31 min.

   På den anden rejseplan er rejsetiden:
   12:50 - 9:41 =
   12 timer + 50 min. - (9 timer + 41 min.) =
   3 timer og 9 min.

   På den tredje rejseplan er rejsetiden:
   13:19 - 9:48 =
   13 timer + 19 min. - (9 timer + 48 min.) =
   4 timer - 29 min. =
   3 timer og 31 min.

   Dermed er den anden rejse med afgang kl. 9:41 den hurtigste.
2. De skal betale for to voksne og et barn.
   Det giver: 2·325,00 kr. + 163,00 kr. = 813,00 kr.
3. Prisen for en voksne på DSB 1° er 488 kr. Prisen for en voksen standard-billet er 325 kr.
   Det antal procent den ene billet er dyrere end den anden er: [(488 - 325)/325]·100 % = [153/325]·100 % = 50,2 %
4. Den procentvise forskel er ikke den samme for alle aldersgrupper, da en 1. klasses
   barnebillet er dobbelt så dyr som standard børnebillet. Denne forskel er større end for voksenbilletten.
5. De samlede udgifter er udgift til benzin + udgift til bro + udgifter til bil i øvrigt =
   (294 km)·(9,95 kr./L)/(15 km/L) + 215 kr. + (294 km)·(2,00 kr./km) = 998 kr.
6. Rejsetiden i timer er antal km divideret med gennemsnitshastighed i km/t. Man får:
   Rejsetid er (294 km)/(98 km/t) = 3 timer
7. Rejsetiden er næsten ens for tog og bil. Forskellen er 9 min.
   Prisen for bil er 998 kr, mens den for tog er 813 kr. dvs. en forskel på 185 kr. eller bil er (185/813)·100 % = 23 % dyrere end tog.

Svar på opgave 4: Amalienborg

1. I 2009 var dronningen (2009 - 1940) år = 69 år
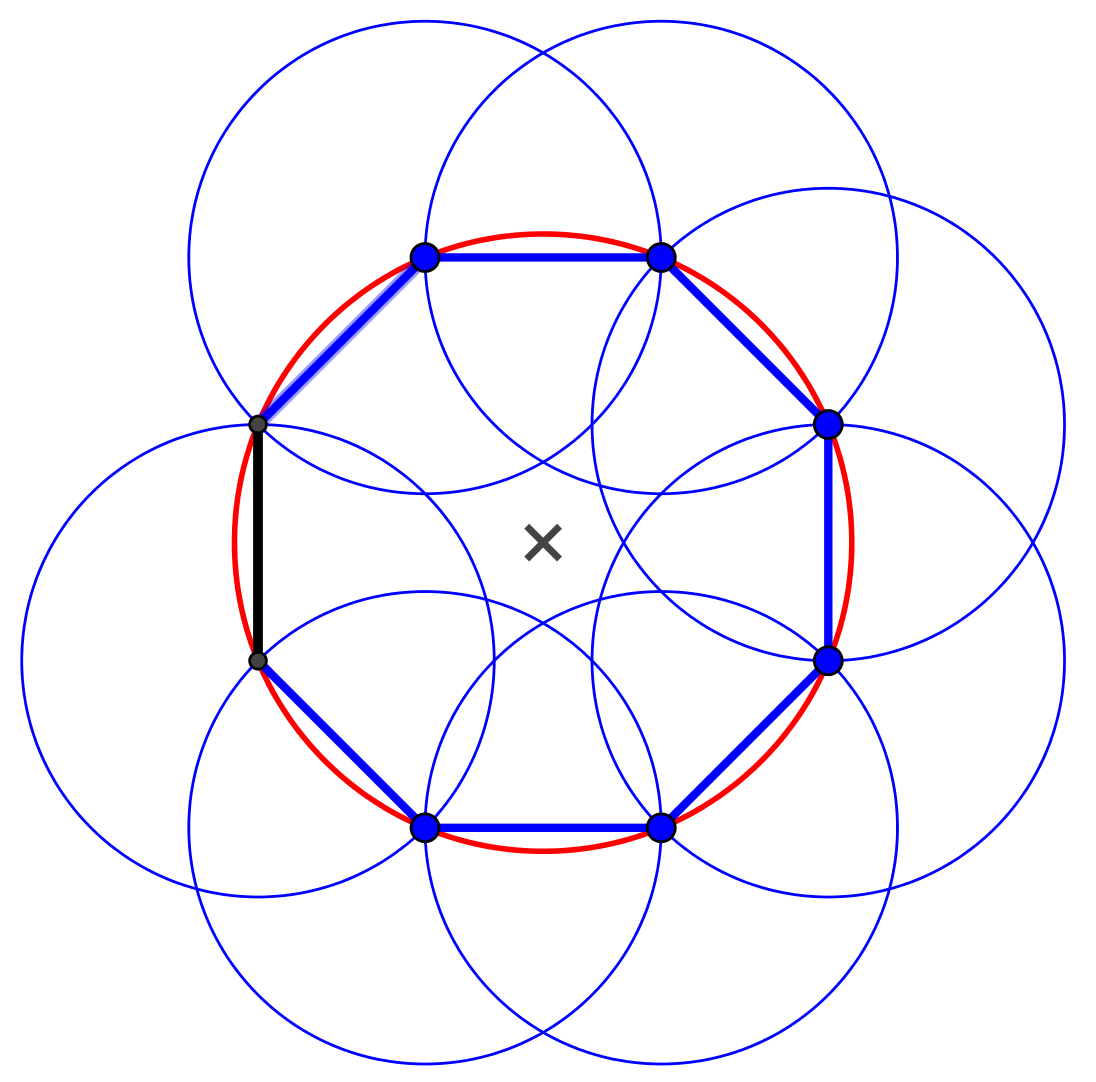
2. Den omskrevne cirkel konstrueres som vist nedenfor, hvor B er det ene endepunkt for siden:
   
3. Resten af den regulære ottekant (vist med blåt) konstrueres ved hjælp af (blå) cirkler, hvis radius er lig med siden i ottekanten.
   
4. Hvis siden af slotspladsen er 6 cm på en tegning, der er tegnet i målestoksforholdet 1:1000, så er siden i virkeligheden 1000·(6 cm) = 6000 cm = 6000·(0,01 m) = 60 m
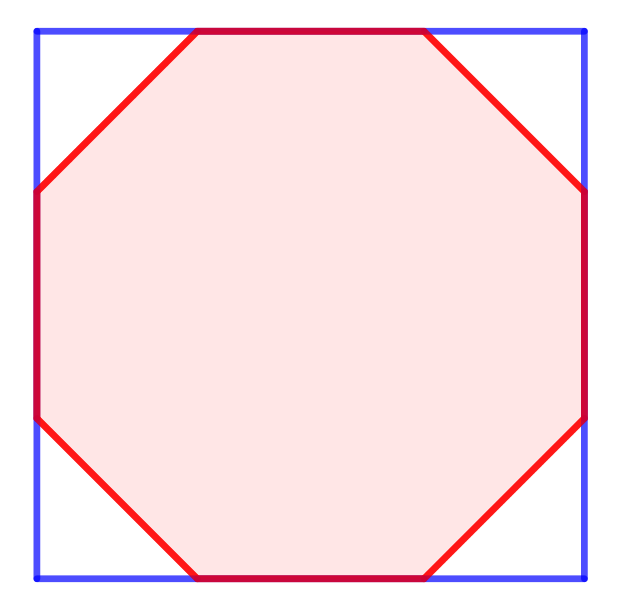
5. Den regulære ottekant er nedenunder vist med rødt. Udenom er tegnet et blåt kvadrat. I hvert hjørne af kvadratet er en retvinklet ligebenet trekant, hvis grundlinje er lig med siden i ottekanten. Arealet af ottekanten kan beregnes ved at trække de små hjørne-trekanters arealer fra kvadratets.
   
6. Sidelængden i ottekanten er 60 m. En katete i en af hjørne-trekanterne er 60/√2 m. Hele det blå kvadrat har dermed siden (60 + 2·60/√2) m = 60·(1 + √2) m.
   Arealet af de fire små retvinklede ligebenede trekanter er: 4·0,5·(60/√2)² m² = 60² m².
   Dermed er ottekantens areal: [60·(1 + √2)]² - 60² m² = (20.982,1 - 3600) m² = 17.382 m²

Svar på opgave 5: Overnatninger i København 2007

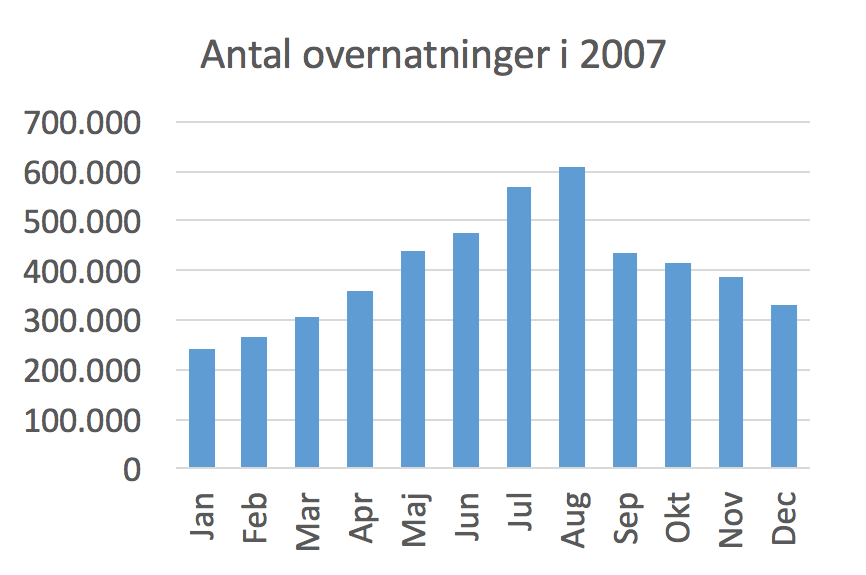
1. Nedenunder er lavet et søjle- eller pindediagram for antallet af overnatninger i 2007.
   
2. Det gennemsnitlige antal overnatninger pr. måned er: samlet antal overnatninger divideret med 12.
   Man får gennemsnittet: 4.827.832/12 = 402.319,3 = 402.319 overnatninger pr. måned.
3. Nedenunder er det gennemsnitlige antal månedlige overnatninger tegnet ind med en rød linje i søjlediagrammet.
   
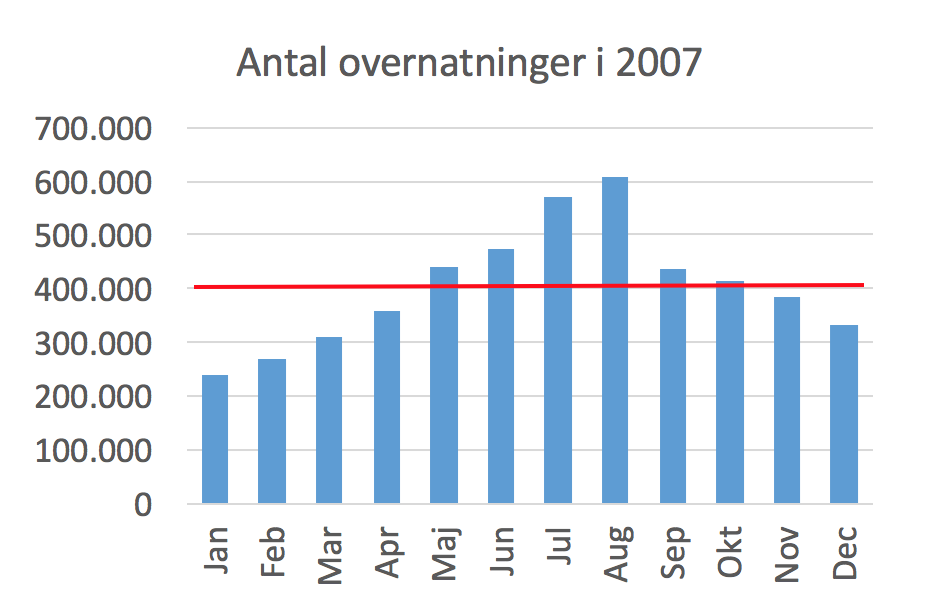
4. Det ses, at overstående diagram, at månederne: maj, juni, juli, august, september og oktober ligger over gennemsnittet.
5. Man antager, at antal overnatninger stiger med 5 % om året fra 2007 til 2015.
   Man skal bruge fremskrivningsformlen: K = K₀·(1 + r)ⁿ.
   Man skal finde K, når K₀ = 4.827.832, r = 5 % = 0,05 og n = 2015 -2007 = 8.
   Man får K = 4.827.832·(1 + 0,05)⁸ = 4.827.832·1,05⁸ = 7.132.905.
   Det vil sige, at turistforeningen forventer, at der er 7.132.905 overnatninger i Danmark i 2015.