Svar på opgave 1: Golf

1. Lis' årlige kontingent er 2·750 kr. = 1500 kr.
2. Den månedlige udgift = 1500kr./12 = 125 kr.
3. Pris i Golfshoppen: (599 + 199 + 4·299) kr. = 1994 kr. Besparelse ved køb i supermarked: (1994 - 1499) kr. = 495 kr.
4. Pris ved rabat i Golfshoppen: 1994·(100% - 20%) kr. = 1994·0,8 kr. = 1595,20 kr. Det vil sige, at prisen i Golfshoppen efter 20 %'s rabat er stadig højere end tilbudsprisen i supermarkedet.
5. Kald rabatten (i procent) for x. Der gælder at:
   1994 - 1994·x = 1499 ⇔
   x = (1994 - 1499)/1994 ⇔
   x = 0,248 ≈ 25 %
   Det vil sige, at rabatten skal være mindst 25 % før, at Golfshoppen er billigere end supermarkedet

Svar på opgave 2: Golfbanen

1. (Kræver måling på papirudgave af eksamenssættet). Målingen skal vise, at længden af den orange pil på billedet nedenunder er (145 m)/2000 = 0.0725 m = 7,25 cm.
   
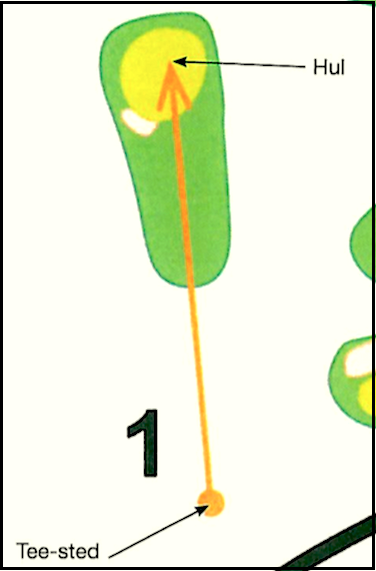
2. På nedenstående billede, som er lavet i Geogebra, er den korteste rute tegnet
   
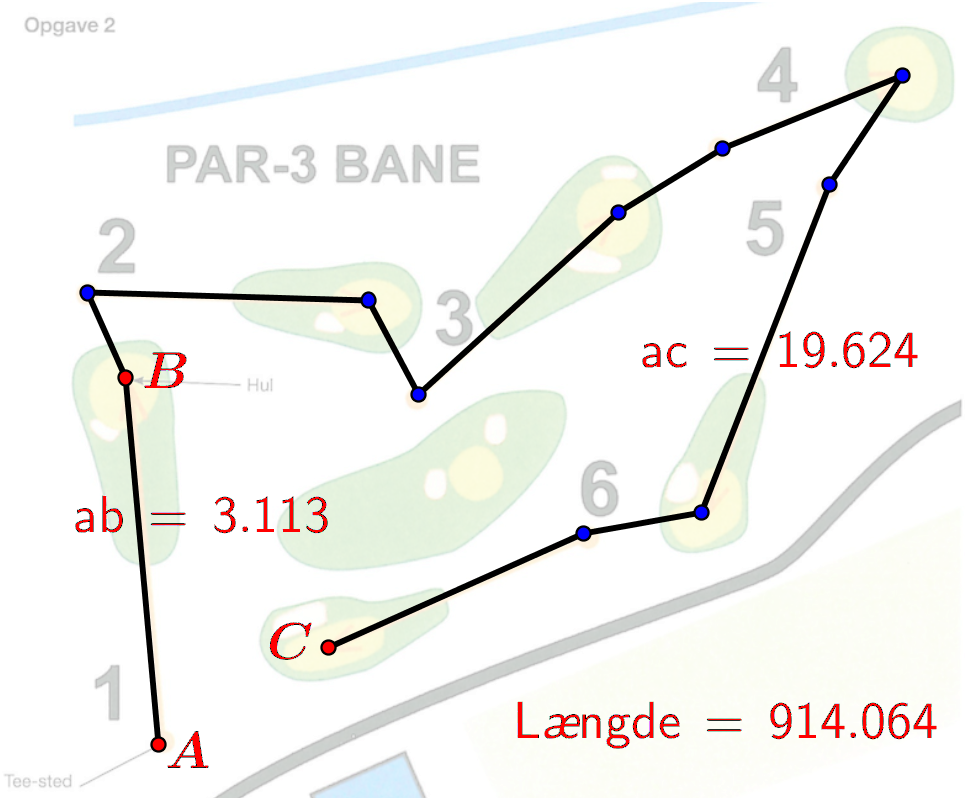
3. På billedet ovenfor er banens længde målt til 19,624 enheder. Længden af 1. hul er målt til 3,113 enheder. Dvs. banen er (19,624/3,113) gange længden af 1. hul eller (19,624/3,113)·145 m = 914 m
4. Lis' samlede score er (5 + 3 + 3 + 5) slag = 16 slag
5. Point: 1. hul: 1 point, 2. hul: 3 point, 3. hul: 3 point og 4. hul: 1 point. I alt antal point: 1 + 3 + 3 + 1 point = 8 point
6. Lis mangler 4 point, som enten kan komme ved 2 point + 2 point eller 1 point + 3 point. Dette giver mulighederne 4 slag + 4 slag eller 3 slag + 5 slag.

Svar på opgave 3: Bolden

1. Den må højst veje: (1,62 ounce)·(28,35 g/ounce) = 45,93 g
2. Kassens indvendige mål er:
   Længde = tre gange diameter af bold = 3·(2·21,5 mm) = 129 mm
   Bredde = dybde = diameter af bold = 2·21,5 mm = 43 mm
3. Kassens rumfang er (129 mm)·(43 mm)·(43 mm) = 238.521 mm³ = 238.521·(0,1·cm)³ = 238.521·(0,1³·cm³) = 238.521·0,001 cm³ = 238,5 cm³
4. 3·(21,5 mm)³·(4π/3) = 3·(2,15 cm)³·(4π/3) = 124,9 cm³
   Andel = (124,9/238,5)·100% = 52 %
5. Nedenstående tegning, som er lavet i Geogebra, viser konstruktionen af den sidste cirkel og de to sidste sider.
   
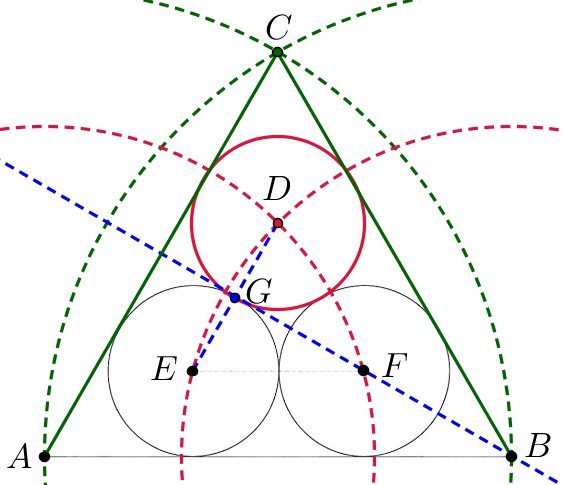
6. Konstruktion af den tredje církels centrum:
   Med A som centrum og AF som radius konstrueres den ene røde cirkel. Den anden røde cirkel konstrueres med B som centrum og BE som radius. De to røde cirkler skærer hinanden i D, som er den tredje cirkels centrum.
7. Kassen er en prisme med en grundflade, der har form af en ligesidet trekant. Rumfanget af et prisme er areal af grundflade gange højde. Højden er diameteren af en bold. En ligesidet trekant har arealet: s²·(√3)/4, hvor s er sidelængden af trekanten.
   Sidelængden findes nemmest ved at måle en sidelængde i Geogebra, måle afstanden mellem centrene i de to givne cirkler og gange forholdet mellem de to tal med diameteren af en golfbold.
   Dette giver følgende værdi af sidelængden s:
   
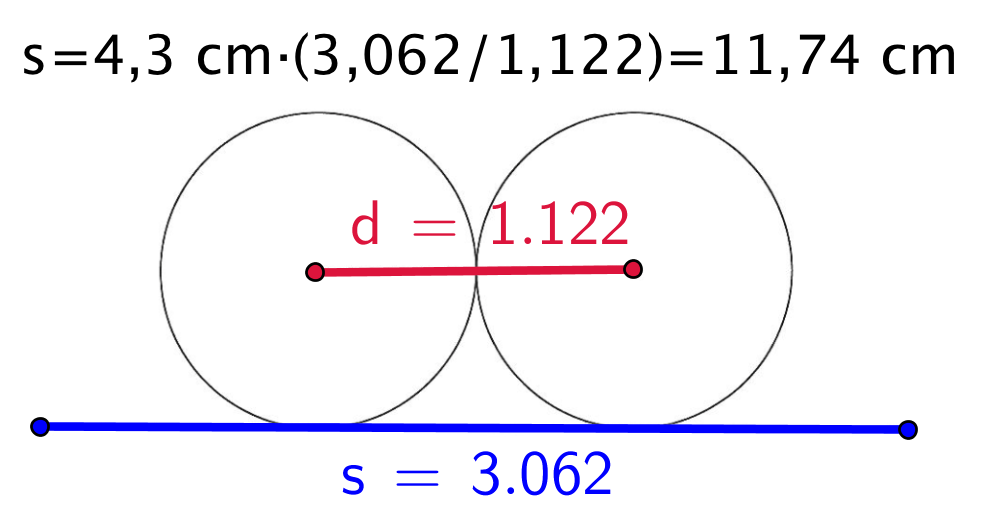
   Rumfanget bliver: højde·grundflade = (4,3 cm)·[(11,74 cm)²·(√3)/4] = 257 cm³

Svar på opgave 4: Medlemstal

1. Antallet af medlemmer aflæses ud fra den blå kurve og venstre lodrette akse til 26.000. Antallet af klubber aflæses ud fra den røde kurve og højre lodrette akse til 52
   Dette er vist på billedet nedenfor:
   
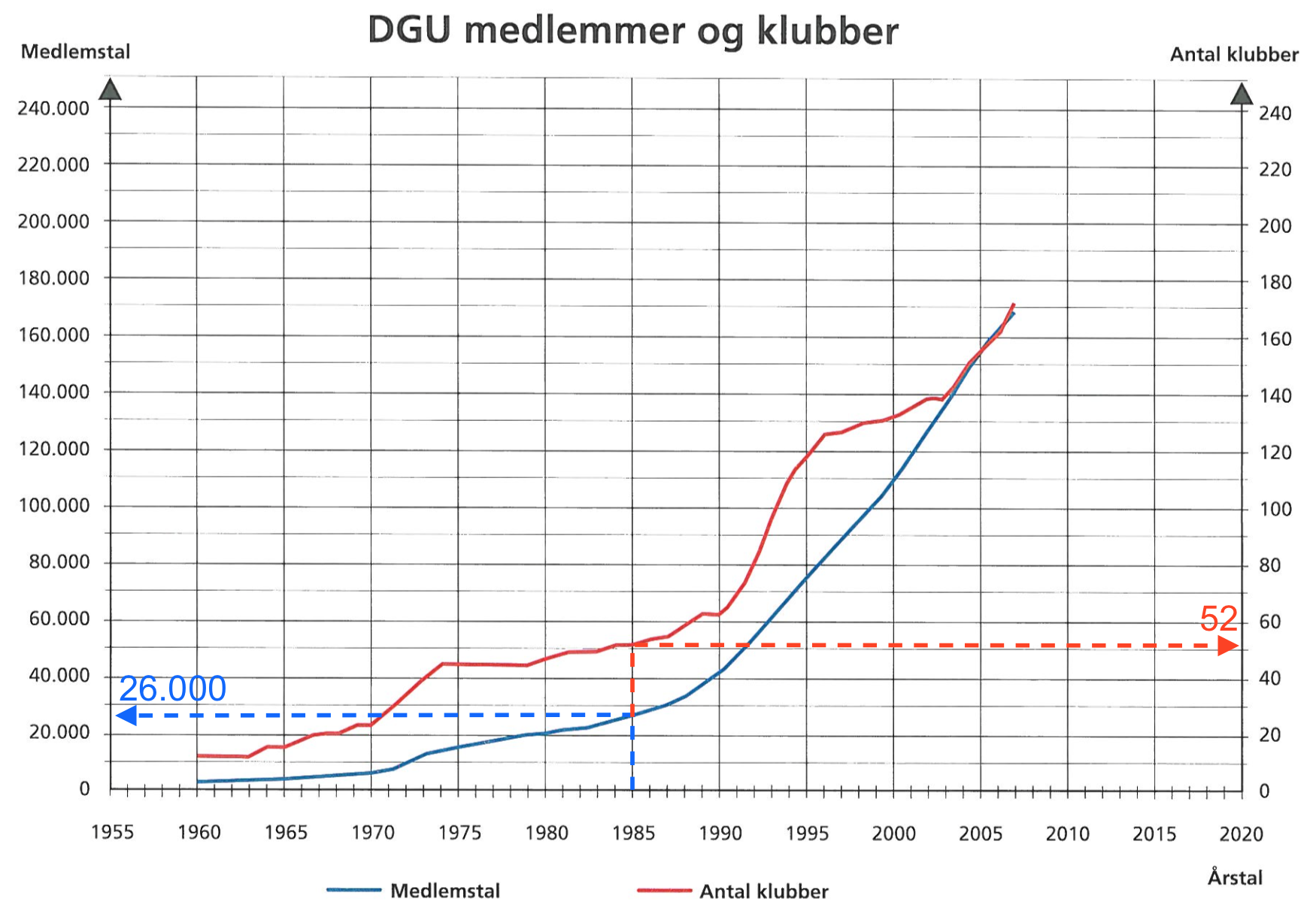
2. Antal medlemmer pr. klub: 26000 medlemmer/52 klubber = 500 medlemmer pr. klub
3. Kurven for medlemstallet (den blå) har den største hældning i 1990'erne.
4. Det ses af, at de to kurver er næsten sammenfaldende, og at der er 1000 ganges forskel på de to akser.
5. Den blå medlemskurve stiger med 30.000 på de fire år fra 2003 til 2007. Dvs. medlemstallet stiger med 7500 om året. Der er otte år fra 2007 til 2015. Stigningen i denne periode vil være 8·7500 medlemmer = 60.000 medlemmer. Dette skal lægges oven i medlemstallet fra 2007 som er 170.000.
   Medlemstallet i 2015 bliver derfor forventningsvis: (170.000 + 60.000) medlemmer = 230.000 medlemmer

Svar på opgave 5: Golfjern

1. Sammenhængen mellem jern-nr. og vinkelmål er vist på nedenstående kurve tegnet i Geogebra. Kun 4 punkter fra tallen er brugt til at tegne kurven, der vist med det sorte linjestykke. Den blå punkterede linje er lavet ud fra to punkter på kurven og er brugt til at få Geogebra til at beregne kurvens ligning. Linjens ligning er er tilføjet til tegningen med blåt.
   
2. Ligningen ses af tegningen at være -4x + y = 8 eller y = 4x + 8
3. Nedenstående tegning er lavet i Geogebra. Enheden på begge akser er meter. Punktet (0,0) er tee-stedet.
   
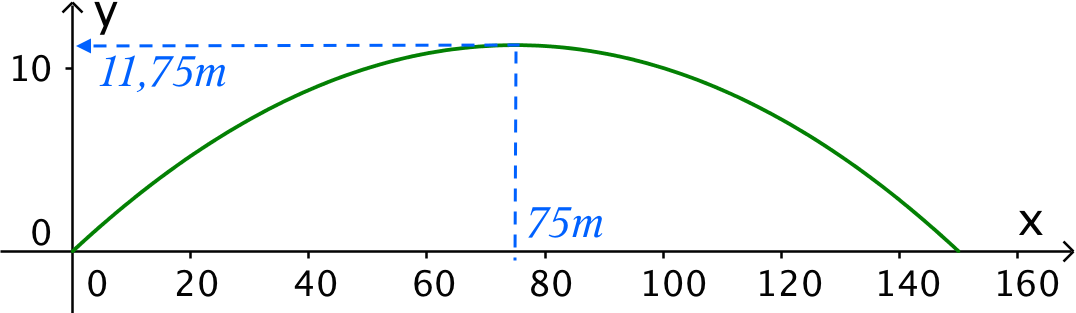
4. Golfbolden går over træet, hvis y-værdien for x = 75 er større end 10 meter. Man indsætter x = 75 i forskriften for boldens højde og får: y = -0,002·75² + 0,3·75 m = 11,75 m. Dette viser, at bolden kommer over træet.