Svar på opgave 1: Indgang

1. De kan være der fra kl. 10 til kl. 18, det vil sige i 8 timer
2. De to lærere kommer gratis ind. Prisen for eleverne bliver: 24·75 kr. = 1800 kr.
3. Den procentvise stigning er [(75 - 70)/70]·100 % = 7,14 %
4. Prisen i 2009 bliver 75 kr. + 75 kr. · 7,14 % = 75·(1 + 7,14 %) kr. = 75·(1 + 0,0714) kr. = 80,36 kr.
5. Man har, at: 100 € = 745 DKK. Adgangsprisen i € bliver: 24·(11 €)·[(745 DKK)/(100 €)] = 1966,80 DKK. Da dette er mere end de 1800 DKK, som skulle betales, hvis man betalte i DKK, er det bedst at betale i DKK
6. Man beregner kursen for alle typer af billetter i tabellen og får:
   Voksen: (150/21,5)·100 = 698.
   Barn: (125/18)·100 = 694.
   Lærer+elev: (75/11)·100 = 682.
   Gruppe: (125/18)·100 = 694.
   Dette viser, at voksenbilletten er udregnet efter den højeste kurs

Svar på opgave 2: Den blå kube

1. Kuben er ikke en terning, da dens kanter ikke er lige lange
2. Det bemærkes, at dugen ikke dækker bunden af kuben. Dugens areal bliver: 4·(19,5 m)·(22,8 m) + (22,8 m)·(22,8 m) = 2298 m²
3. Man skal lægge 5 % til arealet af dugen. Man får: 2298 m² + 2298 m²·(5 %) = 2413 m²
4. For at finde forsvindingspunktet skal man forlænge to vandrette kanter af terningen til de forlængende linjer når horisonten. Skæringspunkterne mellem de forlængede linjer og horisonten er forsvindingspunkterne. Dette er vist nedenunder.
   
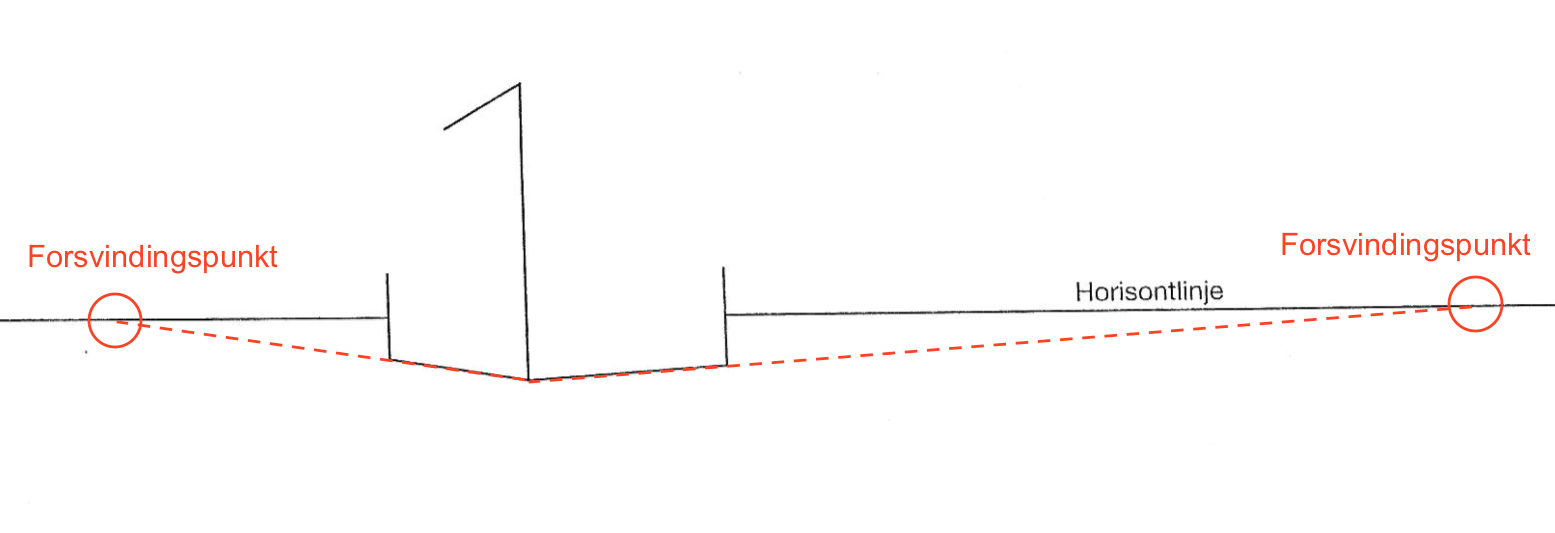
5. For at tegne de manglende linjer på den øverste del af terningen forbindes det øverste hjørne af terningen med hvert forsvindingspunkt og der tegnes to hjælpelinjer langs de to lodrette kanter. Hjælpelinjerne skærer de linjer, der forbinder toppunkt med forsvindingspunkterne i de to sidste hjørner af terningen. De manglende dele af kanterne tegnes op til de fundne hjørner. Dette er vist nedenunder.
   

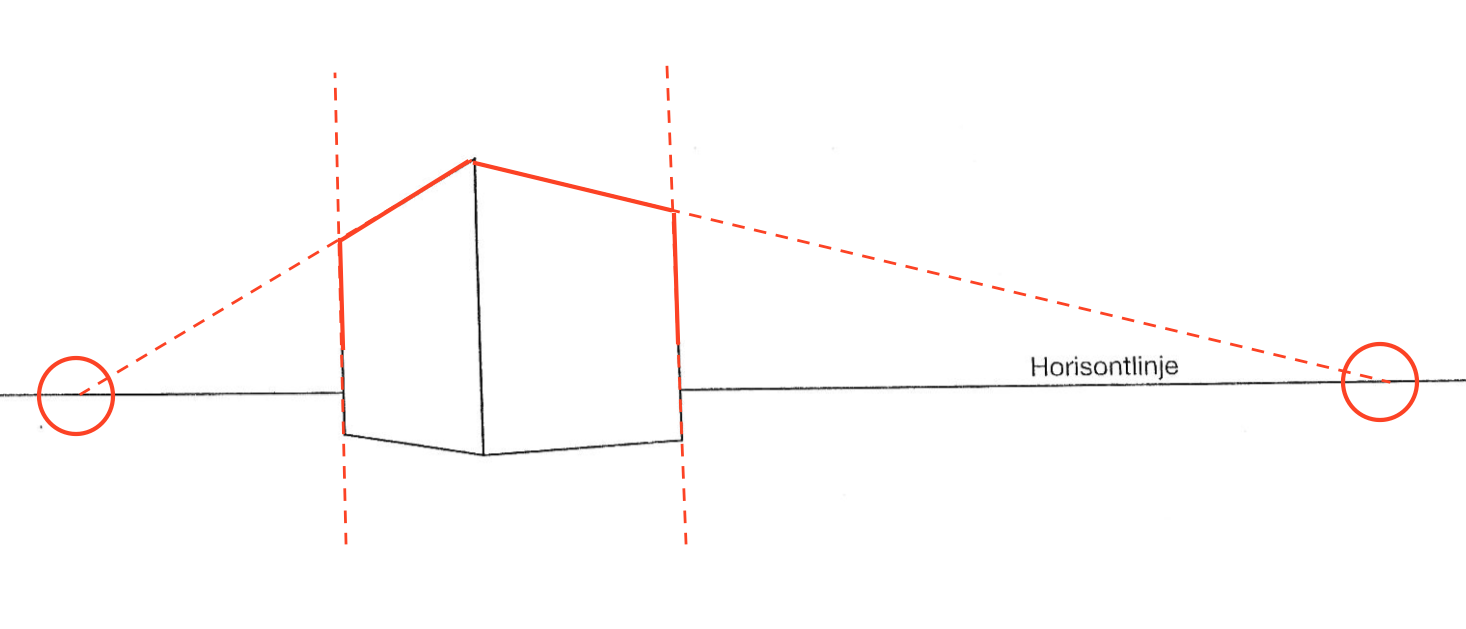
Svar på opgave 3: Cafeen

1. For hvert af de to slags brød er der tre muligheder for pålæg, dvs. 2·3 muligheder = 6 muligheder
2. For hvert af de seks sandwicher er der fem desserter og to slag drikkevarer. Dette giver i alt: 6·5·2 muligheder = 60 muligheder
3. Den del af Peters daglige energibehov, som menuen dækker, er: (4.000 kJ/10.600 kJ)·100 % = 38 %
4. Procentdelene for kulhydrater, protein og fedt skal regnes om til vinkler efter formlen: vinkel i cirkel-diagram = (procentdel som decimaltal)·360°. Man får diagrammet:
   
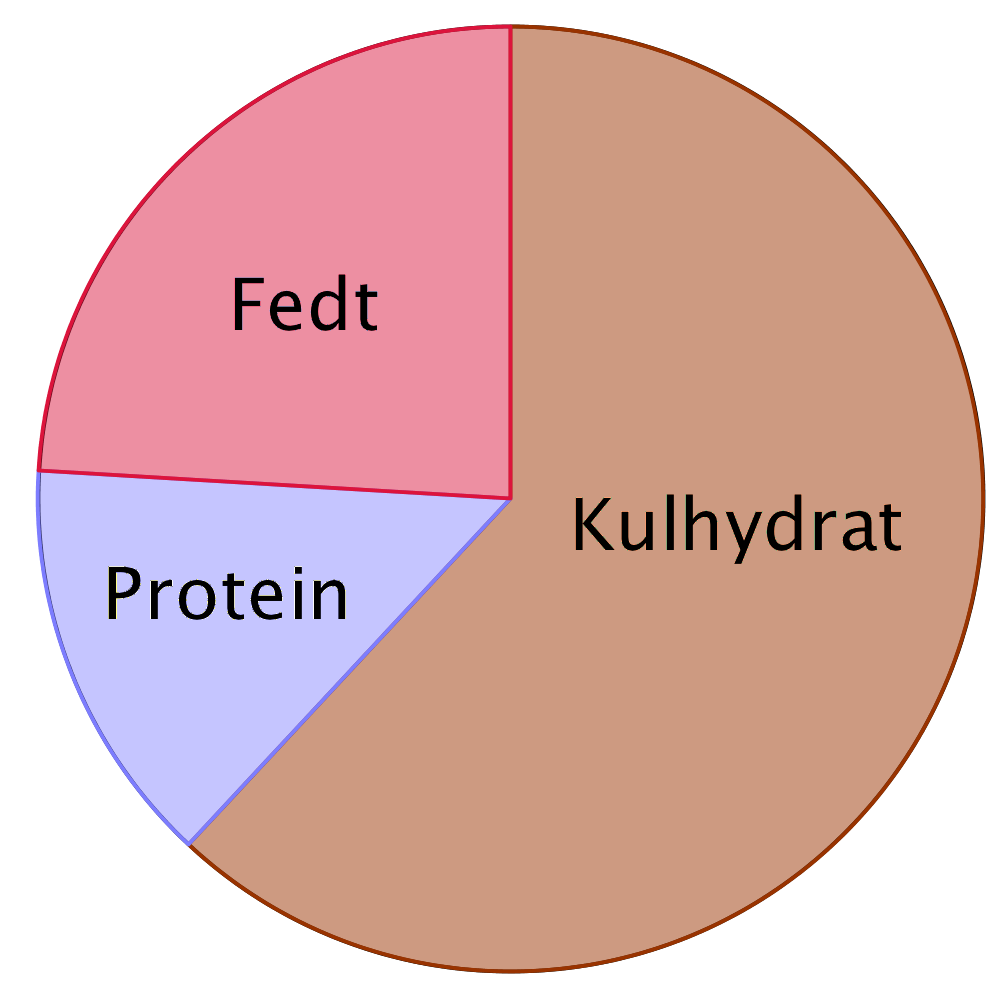
5. På øjemål ser man at cirkel-diagrammet for menuens sammensætning i opgave (3.3) passer med den anbefalede sammensætning på nær, at mængden af protein er lidt for lille og mængden af kulhydrat lidt for stor.
6. Peter forbrænder 1000 kJ/time ved at danse. Han skal forbrænde 1500 kJ og skal dermed danse i 1500 kJ/(1000 kJ/time) = 1,5 time
7. Han kan f.eks. løbe crossløb mm. Dette kræver at han udfører de forskellige sportsgrene i 900 kJ/(2430 kJ/time) = 0,371 time = 0,371·(60 min.) = 22 min.

Svar på opgave 4: Kædepumpen

1. Omkredsen af en cirkel med radius 25 cm = 2·(25 cm)·π = 157 cm = 1,57 m
2. Længden af kæden er 16·(25 cm) = 400 cm = 4,00 m (Der er lige så mange kædestykker, som der er kugler, når kæden hænger sammen i enderne.)
3. Vandet mellem to kugler i røret er afgrænset af en cylinder med diameter 7,7 cm og længden 25 cm. Fra denne cylinder skal trækkes rumfanget af to halve eller en hel kugle som vist nedenunder.
   
   Dette giver: Rumfang af vand: = (25 cm)·π·(7,6 cm/2)² - (4/3)·π·(7,6 cm/2)³ = 904,3 cm³ = 0,9 L
4. Procentdelen er (0,5L/0,9L)·100 % = 56 %
5. Man får følgende kurve, der er tegnet i Geogebra, hvor enheden på y-aksen er L/min...
   
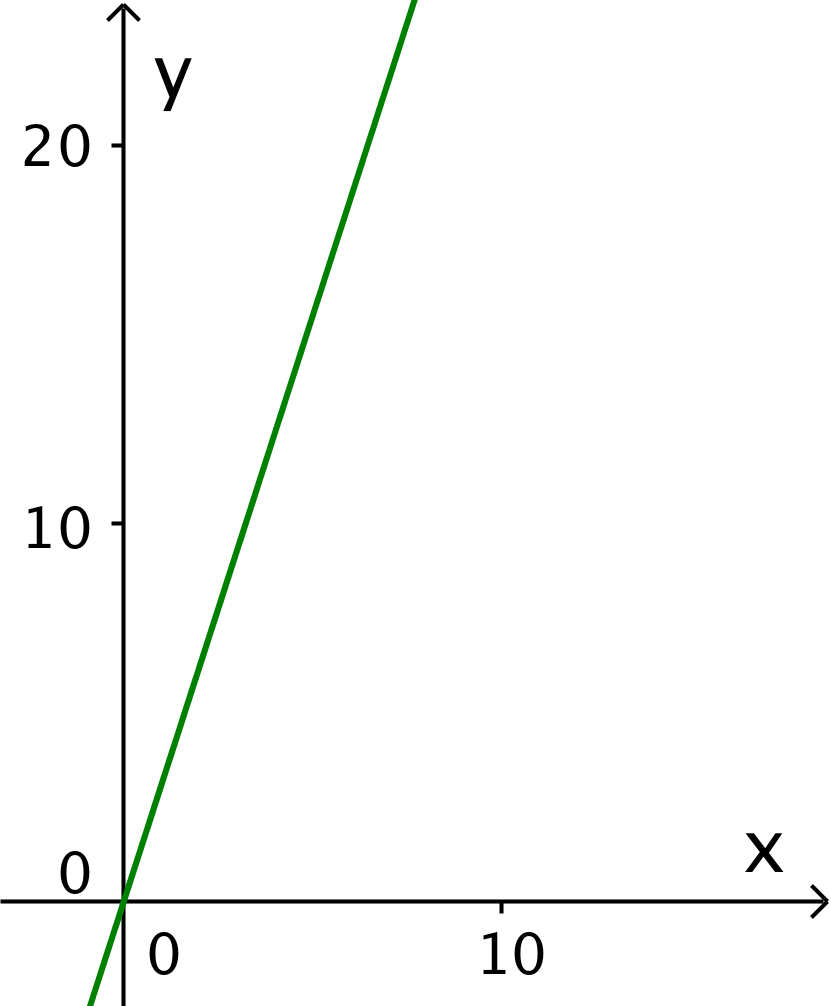
6. Antallet af omdrejninger regnes ud fra formlen til: (46,5 L/min.)/(3,1 L/omdrejning) = 15 omdrejninger/min.
7. Kald antallet af omdrejninger pr. minut for x. De 3 m³ omregnes til 3000 L. Der gælder at den oppumpede mængde vand i L pr. minut er 3,1·x. Man får ligningen for hele mængden af vand:
   3,1·x·60 min. = 3000 ⇒
   x = [3000/(60·3,1)] ⇒
   x = 16
   Det vil sige, at antal omdrejninger pr. minut for eleverne er 16
   

Svar på opgave 5: Granithjul

1. Tykkelsen er den ydre radius minus den indre radius. Den ydre radius er 1,80 m /2 = 0,9 m. Den indre radius er 1,50 m/2 = 0,75 m. Tykkelsen bliver: 0,90 m - 0,75 m = 0,15 m = 15 cm
2. Hjulets rumfang kan beregnes som rumfanget af en ydre cylinder, hvorfra der er trukket en indre cylinder.
   Rumfanget af den ydre cylinder er: (0,45 m)·π·(1,80 m/2)² = 1,145 m³
   Rumfanget af den indre cylinder er: (0,45 m)·π·(1,50 m/2)² = 0,7952 m³
   Rumfanget af hjulet er: 1,145 m³ - 0,7952 m³ = 0,349 m³ = 0,35 m³
3. Massen af granithjulet er rumfanget gange massefylden (omregnet til kg/m³). Man får:
   Masse = 0,35 m³·(2,7 g/cm³) = 0,35 m³·[2,7·(0,001 kg)/(0,01 m)³] =
   0,35·2,7·(0,001)/(0,01·0,01·0,01)³ (m³/m³)·kg =
   0,35·2,7·0,001·1.000.000 kg = 0,35·2,7·1000 kg = 945 kg
4. (Kræver papirtegning.) Man skal lave en tegning som nedenstående (i Geogebra), hvor hjulets ydre diameter er 9 cm.