Folkeskolens problemregning for 9. klasse, december 2007 | Gå til oversigt

Svar på opgave 1: Modeljernbanen

  1. Prisen er: 643 kr. + 2·(18 kr.) = 679 kr.
  2. Den tyske pris omregnes til kr. for at sammenligne: (130,86 €)·(7,45 kr./€) = 974,91 kr.
    Det vil sige, at lokomotivet er billigere i Tyskland
  3. Modellens længde er: (18,9 m)/160 = 0,118 m = 11,8 cm
  4. Banens størrelse på den længste led er 2·(19,2 cm) + 33,3 cm = 71,7 cm. På tegingen svarer det til: (71,7 cm)/4 = 17,9 cm. Dette er tegnet nedenunder:
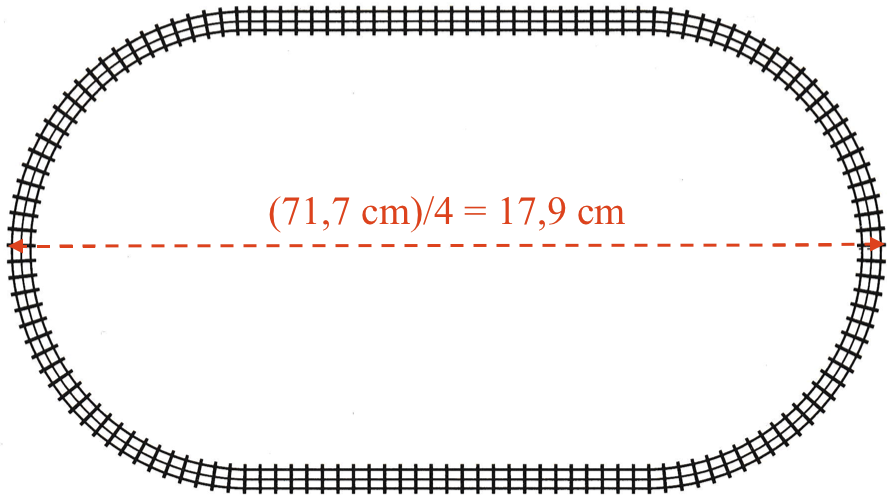
  5. Banens omkreds består af en cirkel med radius 19,2 cm plus to lige stykker med længden 33,3 cm.
    Det vil sige, at banens omkreds er 2·π·(19,2 cm) + 2·33,3 cm = 187,2 cm
  6. Fart er distance divideret med tid. Det vil sige, at togets fart er: (1,872 m)/(10 s) = 0,187 m/s
  7. Modeltogets fart er i følge formlen: (133·1000)/(160·3600) m/s = 0,23 m/s
  8. Tid er lig med distance divideret med fart. Det vil sige, at den tid, som modeltoget er om at tilbagelægge strækningen, er: (1,872 m)/(0,2309 m/s) = 8,1 s

Svar på opgave 2: Graffiti på S-togene

  1. Antallet af rensede togvogne i 2002 var 3750, hvilket aflæses af figuren i opgaven som vist:
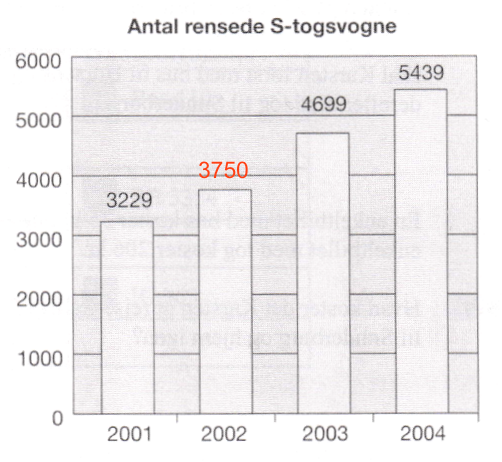
  2. Forskellen mellem antal rensede vogne i 2003 og 2004 er: 5439 - 4699 = 740
  3. Den procentvise stigning i antallet af rensede vogne fra 2003 til 2004 er: [740/4699]·100 % = 15,7 %
  4. Der blev kørt 1147 vognsæt på værksted, og der skal bruges 10089 timer på rensning. Den samlede pris for dette er:
    1147·(411 kr.) + 10089·(1542 kr.) = 16.028.655 kr. = 16 mio kr.
  5. Antallet af timer, som blev brugt til rensning kaldes x. Af tabellen fremgår det, at antallet af vognsæt, som skulle køres på værksted var 1338. Dette giver følgende ligning, der skal løses med hensyn til x :
    12.198.186 = 1338·411 + x·1542 ⇔
    x·1542 = 11.648.268 ⇔
    x = 11.648.268/1542 ⇔
    x = 7554
    Det vil sige, at der blev brugt 7554 timer til rensning i 2006.

Svar på opgave 3: Persontransport

  1. Karsten skal købe to enkeltbilletter til tog og to til bus for at komme frem og tilbage.
    Billetterne koster 2·(35 kr.) + 2·(206 kr.) = 482 kr.
  2. Han rejser hver fjerde weekend eller hver fjerde uge. Der regnes med 52 uger på et år. Dvs. han rejser 52/4 = 13 gange om året.
    Dette giver ham i alt følgende årlige udgifter: 13·(482 kr.) = 6.266 kr.
  3. Antallet af rejser om året kaldes x. Med wildcard koster rejserne ham om året i kr.:
    175 + x·2·35 + x·2·206 - x·2·206·(25 %) =
    175 + x·2·35 + x·2·206·0,75 =
    175 + x·379.
    Uden wildcard koster rejserne i kr.: x·482.
    Man skal finde det x, der gør, at rejserne med og uden wildcard koster det samme. Man får:
    175 + x·379 = x·482 ⇔
    x = 175/(482 - 379) ⇔
    x = 1,7
    Dette skal rundes op til 2. Det vil sige, at Karsten skal foretage 2 rejser om året for, at det kan betale sig for ham at bruge wildcard.
  4. Rejserne koster ham om året: 175 kr. + 13·(379 kr.) = 5102 kr.
  5. Karstens besparelse i procent med wildcard er: [(6266 - 5102)/6266]·100 % = 18,6 %
  6. Han tager afsted 17:15 og ankommer 21:17. Rejsen varer: 21:17 - 17:15 =
    21 timer + 17 min. - (17 timer + 15 min.) =
    (21 - 17) timer + (17 - 15) min. =
    4 timer + 2 min.
    Det vil sige, at turen tager 4 timer og 2 min.
  7. I Horsens er ventetiden:
    18 timer + 3 min. - (17 timer + 50 min.) =
    (18 - 17) timer + (3 - 50) min. =
    1 time - 47 min. = 13 min.
    I Kolding er ventetiden:
    19:47 - 19:13 =
    19 timer + 47 - (19 timer + 13 min.) = 34 min.
    Det vil sige, at Karstens ventetid er i alt: (13 + 34) min. = 47 min.

Svar på opgave 4: Godstog

  1. Den samlede længde er i følge svararkets tabel: (23,3 + 23,3 + 14 + 14 + 13,9 + 19,9 + 19,9 + 19,9 + 18,9) m = 167,1 m
    Den samlede vægt er: (26,5 + 26,5 + 13,5 + 13,5 + 12,5 + 25,4 + 25,4 + 25,4 + 101,6) tons = 270,3 tons
  2. Bremsevægten er 472,6 tons, som ses af svararkets tabel. Bremsetallet er (472,6/270,3)·100 = 174,8
  3. Toget bremselængde er: (2,765·110 + 0,048·168)2/119 m = 819,1 m
  4. Man skal løse følgende ligning med hensyn til v:
    (2,765·v + 0,048·168)2/119 = 1000 ⇔
    (2,765·v + 8,064)2 = 1000·119 ⇔
    2,765·v + 8,064 = ±√[1000·119] ⇔
    2,765·v = -√[1000·119] - 8,064 eller 2,765·v = √[1000·119] - 8,064 ⇔
    v = −353,0/2,765 eller v = 336,9/2,765 ⇔
    v = −127,7 eller v = 121,8
    Da farten skal være positiv, får man, at togets fart højst må være 121,8 km/t
  5. Nedenfor er grafen for y = 420/x tegnet på svararket i Geogebra.
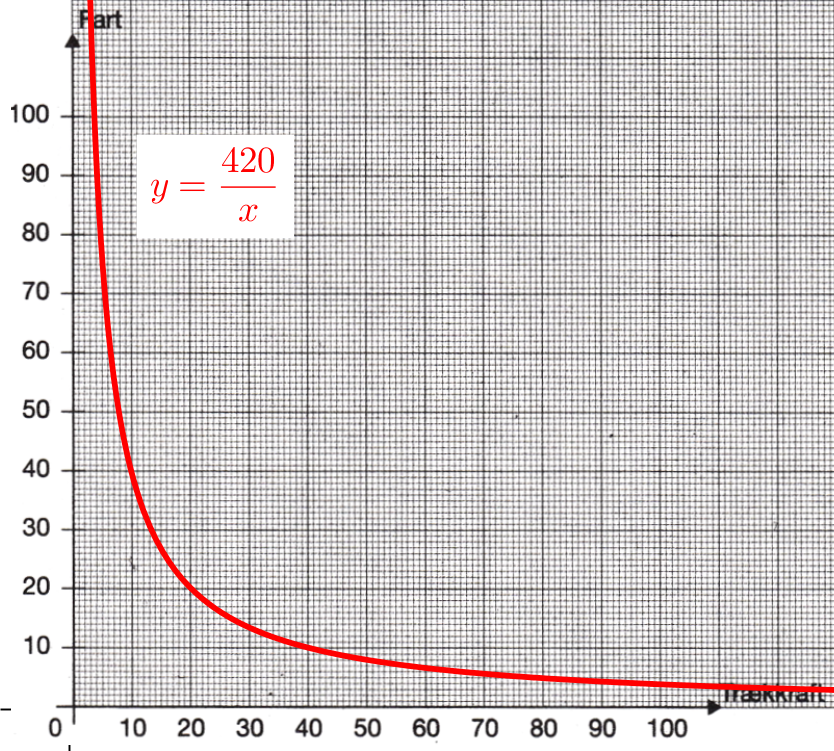
  6. Trækkrafen er: 1200·[0,001 + (10/1000)] tons = 13,2 tons
  7. Man skal bruge formlen for sammenhængen mellem trækkraft (x) og fart (y): y = 420/x.
    Farten y = (420/13,2) km/t = 31,8 km/t