Svar på opgave 1: Mursten

1. I 2007 var det (2007 - 1160) år siden = 847 år siden
2. Tårnet blev bygget for (2007 - (-600)) år siden = 2607 år siden
3. Murstenens rumfang er (22,8 cm)·(10,8 cm)·(5,4 cm) = 1329 cm³
4. Murstenens massefylde er dens masse divideret med dens rumfang. Det vil sige, at massefylden er (2,3 kg)/(1329 cm³) = (2300 g)/(1329 cm³) = 1,73 g/cm³
5. Målestoksforholdet er 5,7:22,8 = 1:4
6. Radius af et hul = 1,2 cm. Massen af mursten med huller kan findes ved at tage massen af en mursten og trække massen af de cylinderformede stykker mursten, der kunne have siddet i hullerne. Massen af en cylinder beregnes som cylinderens rumfang gange murstenens massefylde. Man får at rumfanget er π·(1,2 cm)²·(5,4 cm) = 24,43 cm³. Massen af et stykke af en mursten med dette rumfang er (24,43 cm³)·(1,73 g/cm³) = 42,26 g. Tre gange denne masse er 3·42,26 g = 126,79 g.
   Massen af en mursten med huller er dermed: (2300 - 126,79) g = 2173,2 g
7. Figuren viser et lag mursten set ovenfra, som er stablet på den smalle kant. Det ses, at der er plads til 16 mursten i et lag eller 7·16 = 112 i alt i de 7 lag.
   

Svar på opgave 2: Murstenen brændes

1. Massen af vand som forsvinder ved tørring og forbrænding er: (3,1 - 2,3) kg = 0,8 kg
2. Det procentvise fald i murstenens masse er [(0,8 kg)/(3,1 kg)]·100 % = 25,8 %
3. Vognene har en længde af 2,5 m/vogn og fylder en strækning på 75 m. Det giver følgende antal vogne: (75 m)/(2,5 m/vogn) = 30 vogne
4. Den laveste temperatur er 20 °C og den højeste temperatur er 1050 °C
   Dette er tegnet ind på nedenstående figur:
   
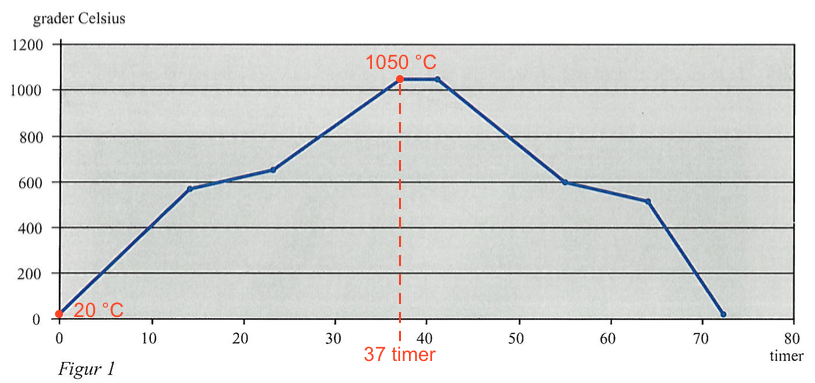
5. Det ses af ovenstående tegning, at den højeste temperatur indtræder efter ca. 37 timer
6. Vognen bevæger sig 75 m på 72 timer (tiden aflæses af førsteaksen på ovenstående tegning). Dette giver en hastighed på 75 m/(72 time) = 1,04 m/t
7. Vognens fart i km/t bliver: 1,04 m/t = 1,04 (0,001 km)/t = 0,001 km/t

Svar på opgave 3: Muren

1. 3 skifte fylder 20 cm. På 2,6 m er der plads til [(260 cm)/(20 cm)]·3 skifte = 39 skifte
2. Man ved at 3 lag mursten med 3 vandrette fuger har højden 20 cm. Et lag mursten har højden 5,4 cm. Man kalder tykkelsen (eller højden) af en fuge for x og løser følgende ligning:
   3·(5,4 cm) + 3x = 20 cm ⇔
   3x = 20 cm - 3·(5,4 cm) ⇔
   x = 3,8/3 cm ⇔
   x = 1,27 cm
   Det vil sige, at tykkelsen af en fuge er 1,27 cm
3. Et forbandt består af 3 lodrette fuger, 2 løbere og 1 kop. Dette betyder at et forbandt måler:
   3·12 mm + 2·22,8 cm + 10,8 cm = 3·1,2 cm + 2·22,8 cm + 10,8 cm = 3,6 cm + 45,6 cm + 10,8 cm = 60 cm
4. For at finde antallet af forbandter skal man løse ligningen:
   60·x - 1,2 = 1260 cm ⇔
   60·x = 1260 + 1,2 cm ⇔
   x = (1260 + 1,2)/60 cm ⇔
   x = 20,98 cm
   Det vil sige, at antallet af forbandter bliver 21
5. Man får formlen: y = (22,8 + 2·10,8 + 3·1,2)·x - 1,2 ⇒ y = 48·x - 1,2
   hvor y er murens længde og x er antallet af forbandter med 1 løber og 2 koppe.

Svar på opgave 4: Tegltag

1. Huset tegnet færdig i Geogebra:
   
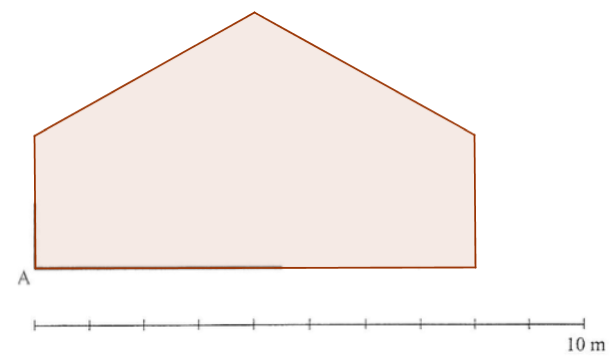
2. Topvinklen i taget kan måles til 120,2 ° i Geogebra som vist:
   
3. Længden s af den skrå side kan beregnes ved hjælp af Pythagoras læresætning. Man kan indtegne en retvinklet trekant som vist:
   
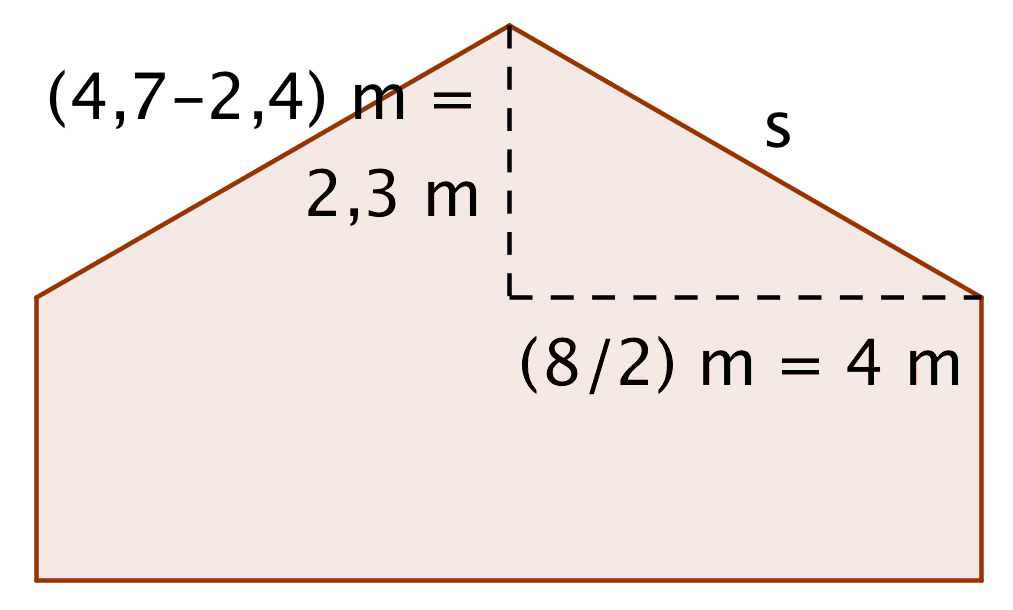
   Af denne tegning ser man, at s = √(4² + 2,3²) m = 4,61 m
4. Man skal finde arealet af hele taget i kvadratmeter og gange med antal sten pr. kvadratmeter. Man skal huske, at der er to tagflader.
   Arealet af taget er 2·(4,61 m)·(14 m) = 129,08 m². Antallet af tagsten bliver:
   129,08 m²·14,3 sten/m² = 1845,8 sten = 1846 sten
5. Antallet af sten, som skal købes er x. Der gælder:
   x - x·1,5 % = 1846 sten ⇔
   x·(1 - 0,015) = 1846 sten ⇔
   x = (1846/0,985) sten ⇔
   x = 1874 sten
   Det vil sige, at der skal købes 1874 sten fra starten for, at de skal række.

Svar på opgave 5: Statistik og boligen

1. Forskellen på antallet af parcelhuse 1997 og 2006 er 1.019.387 - 961.583 = 57.804
2. Den procent vise stigning i antal huse er (57.804/961.583)·100 % = 6 %
3. Nedenstående cirkeldiagram er lavet i Geogebra og viser sammensætningen af hustyper i 2006. Blå: enfamilieshuse, rød: række-, kæde og dobbelthuse; gul: lejligheder og flerfamiliehuse.
   
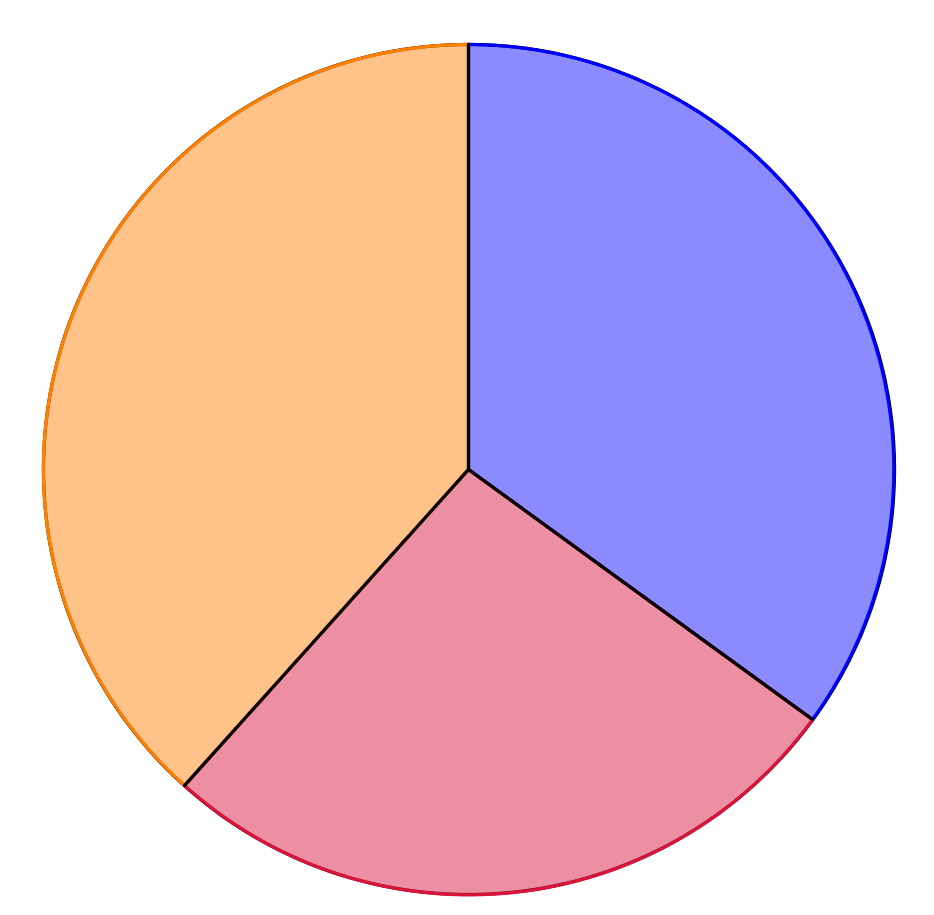
4. Sammenlignet med 2001 er andelen af fritliggende enfamiliehuse større i 2006. Andelen af række-, kæde og dobbelthuse er omtrent uændret, mens andelen af lejligheder og flerfamiliehuse er blevet mindre.