Svar på opgave 1: Vikingeskibe

1. Alderen på skuldelev 2 skibet var i 2006: (2006 - 1040) år = 966 år
2. I Geogebra kan man måle udgravningens omkreds i enheder.
   
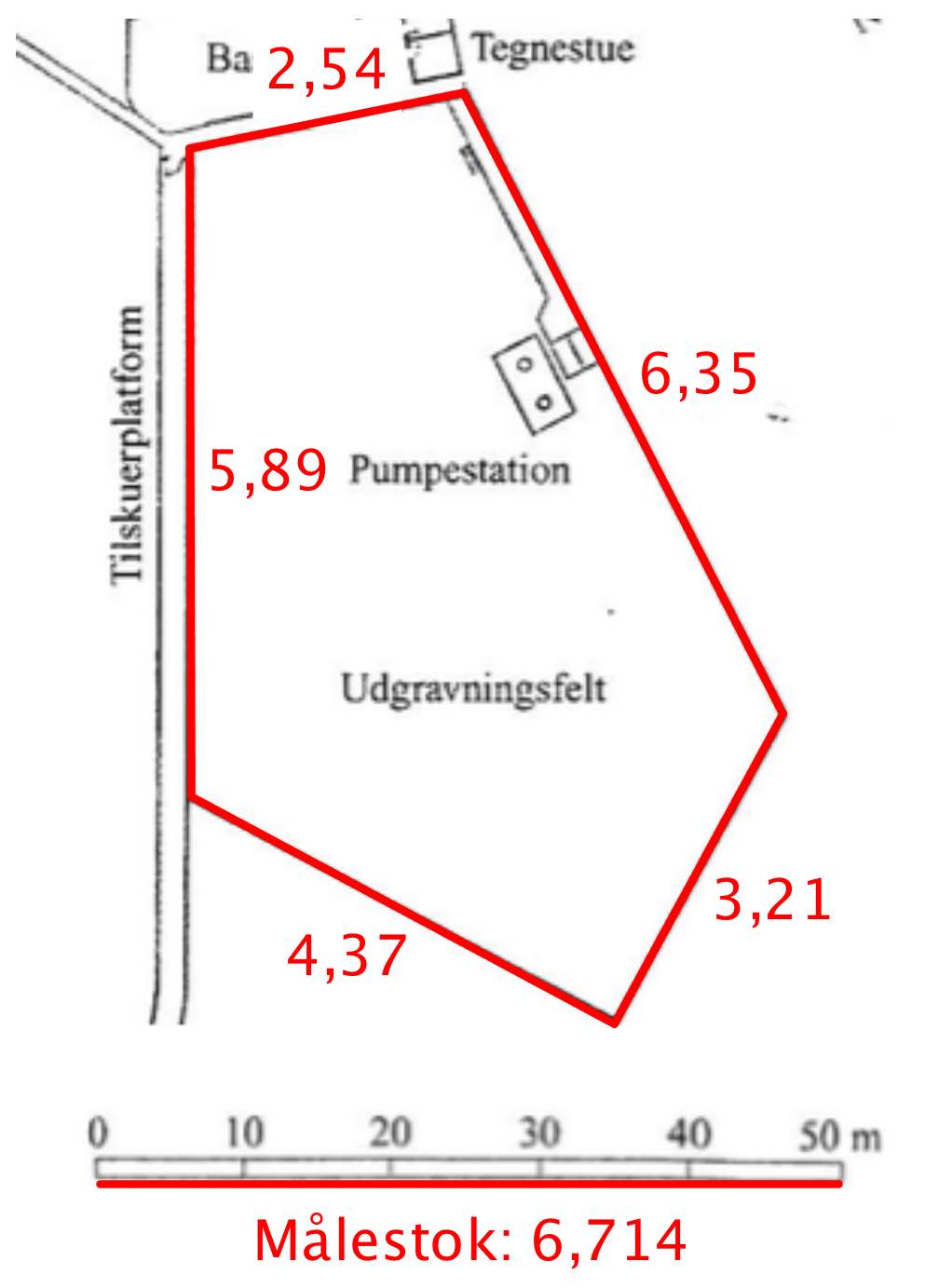
   Antal enheder: 2,54 + 6,35 + 3,21 + 4,37 + 5,89 enheder = 22,36 enheder. Målestokken er på 6,714 enheder, der svarer til 50 meter i virkeligheden.
   Det vil sige, at omregningsfaktoren mellem enheder i Geogebra og meter i virkeligheden er: (50 m)/(6,714 enheder) = 7,447 m/enhed.
   Omkreden af udgravningen er derfor: (22,36 enheder)·(7,447 m/enhed) = 167 m
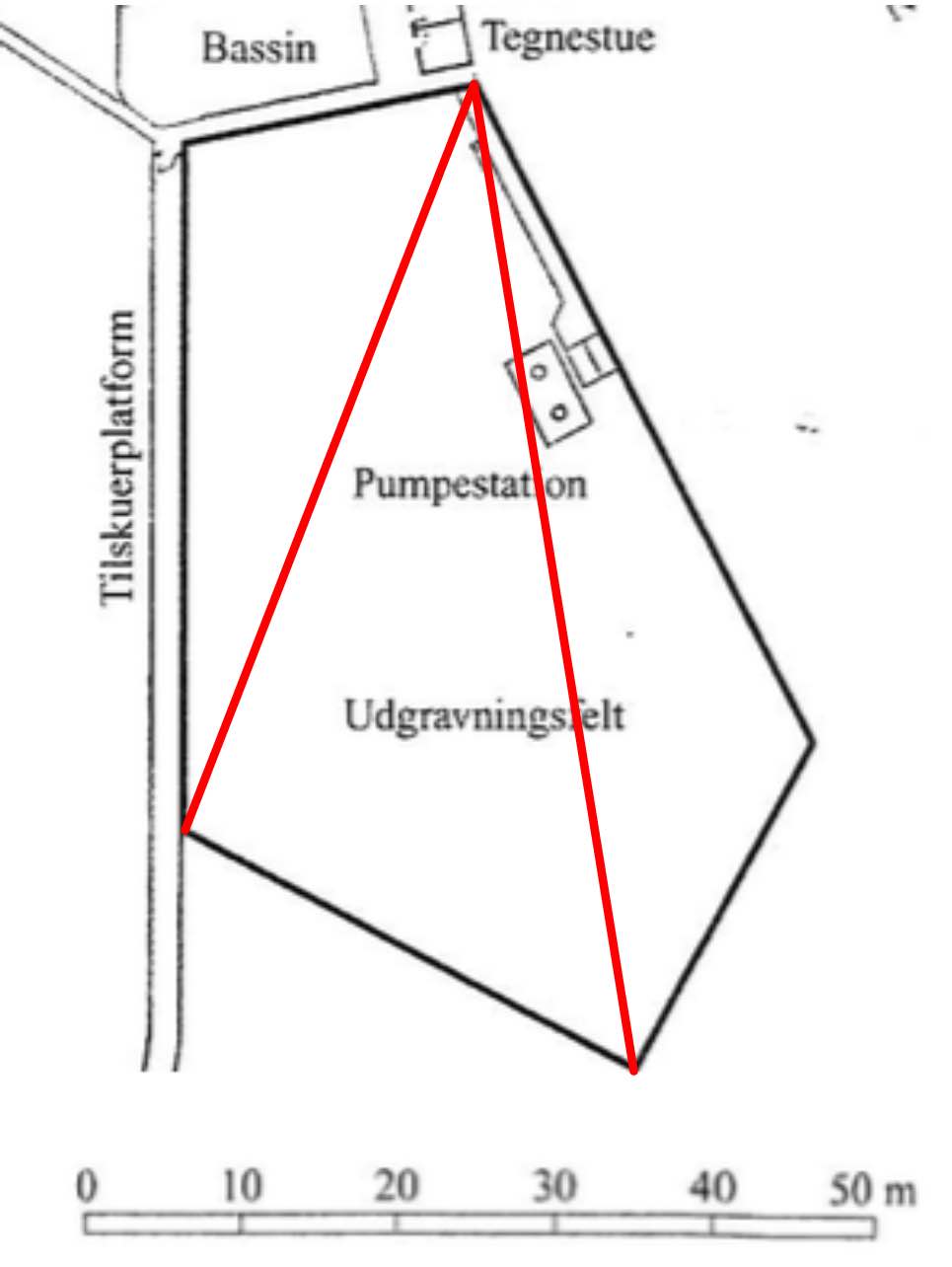
3. Udgravningen kan f.eks. inddeles i 3 trekanter som vist nedenunder.
   
4. Arealet af udgravningen beregnes ud fra arealerne af de 3 trekanter. Deres grundlinjer og højder fremgår af nedenstående figur. Tallene bygger på en tilfældig valgt måleenhed i Geogebra.
   
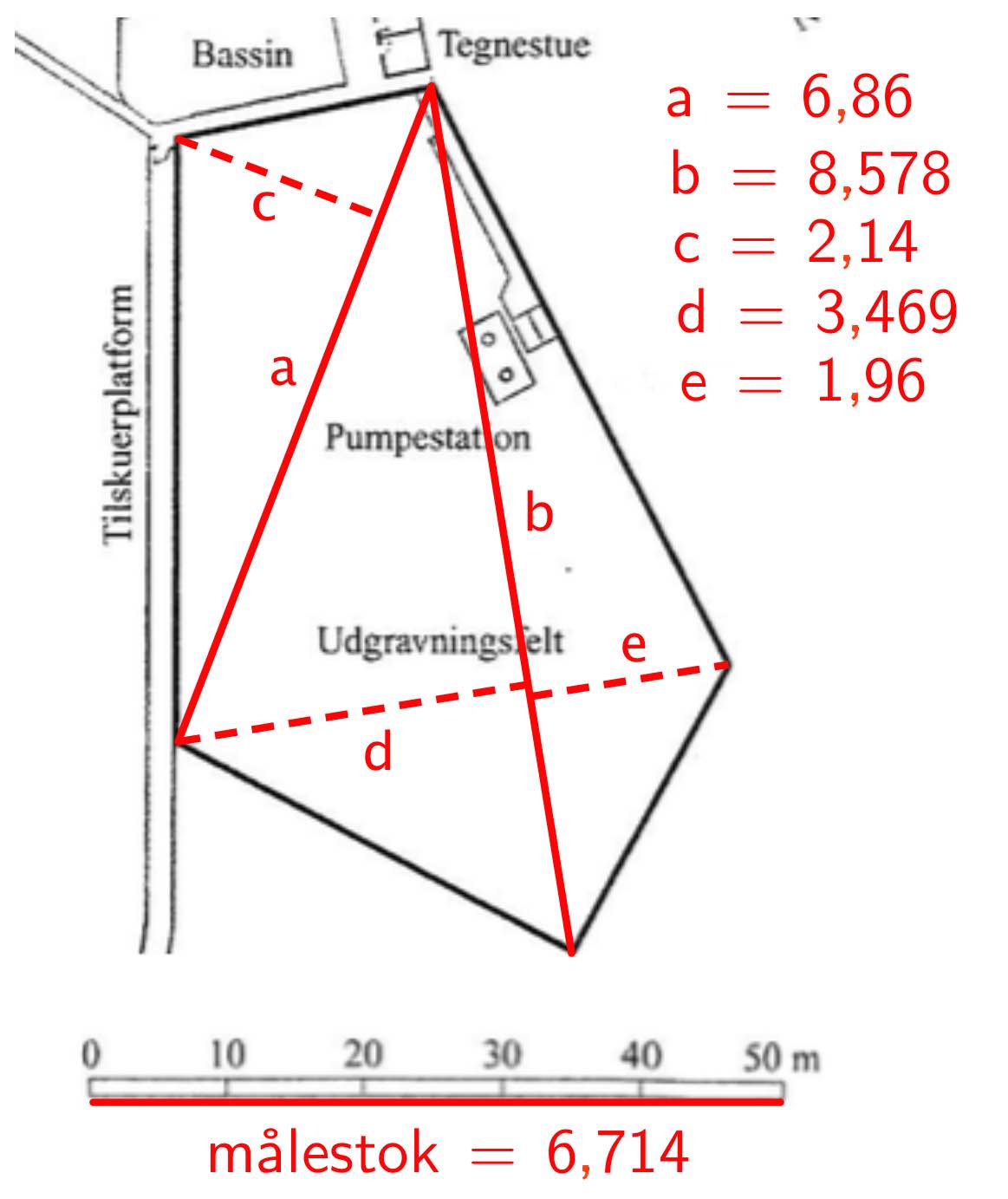
   Som vist svarer 50 m i virkeligheden til 6,714 måleenheder i Geogebra.
   De angivne mål er, omregnet til m:
   a = 6,86·(50/6,714) = 51,09 m
   b = 8,578·(50/6,714) = b=63,88 m
   c = 2,14·(50/6,714) = 15,94 m
   d = 3,469·(50/6,714) = 25,83 m
   e = 1,96·(50/6,714) = 14,60 m
   Arealet af udgravningen bliver, målt i kvadratmeter: 0,5·[51,09·15,94 + 63,88·25,83 + 63,88·14,60] = 1698,5 m².
   Dermed får man at udgravningens areal er (30,625 enhed²)·(55,458 m²/enhed²) = 1.698 m²
5. Forhold mellem længde og bredde:
   16,5/4,5 = 3,67
   29,4/3,8 = 7,74
   14,1/3,4 = 4,15
   17,5/2,5 = 7,00
6. Krigsskibe er lange og smalle, mens handelsskibe er korte og brede.

Svar på opgave 2: Havhingsten sejler

1. Skibets egenvægt udgør: [(8,3 tons)/(22 tons)]·100 % = 38 %
2. Antal mand ombord kaldes x. Der gælder følgende ligning:
   22 t = 8,3 t + 1,6 t + 7,8 t + x·0,09 t/mand ⇔
   22 t - 17,7 t = x·0,09 t/mand ⇔
   x = (4,3 t)/(0,09 t/mand) = x ⇔
   x = 48 mand
   Det vil sige, at der er 48 mand ombord
3. Man bruger samme ligning som før, hvor man ved at antal mand er 80, og skal nu finde den vægt, y, der fjernes fra ballasten. Man får
   22 tons = 8,3 tons + 1,6 tons + (7,8 tons - y) + (80 mand)·0,09 tons/mand ⇔
   y = 8,3 tons + 1,6 tons + 7,8 tons + (80 mand)·0,09 tons/mand - 22 tons ⇔
   y = 24,9 tons - 22 tons ⇔
   y = 2,9 tons
   Det vil sige, at der skal fjernes 2,9 tons fra ballasten
4. 5 knob svarer til 5·0,515 m/s = 2,6 m/s
5. Man får: 2,6 m/s = [2,6 0,001 km]/[(1/3600) time] = 2,6·0,001·3600 km/t = 2,6·3,6 km/t = 9,36 km/t
6. Nedenstående tegning markerer med rødt, at Havhingsten kan sejle med 8,8 knob i 120° vindretning.
   
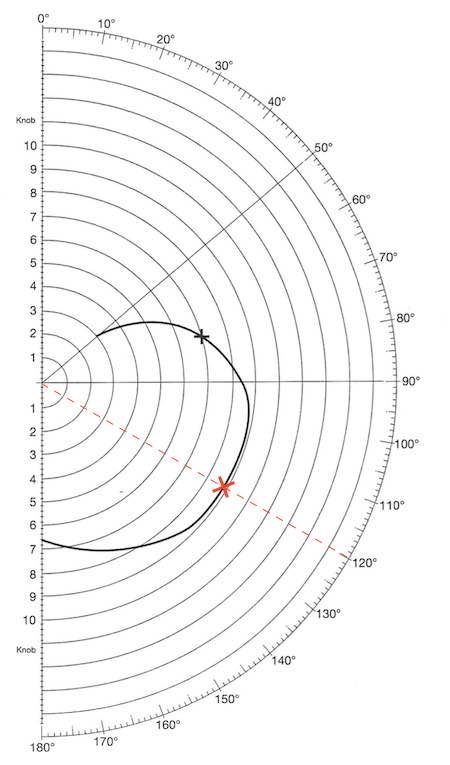
   (Havhingstens sejl er i centrum af cirklen, og dens forende peger opad. En vindretning på 0° er direkte modvind, og 180° er direkte medvind.)
7. Nedenstående tegning viser det interval af vindretninger, som giver Havhingsten en fart på mere end 8 knob,
   
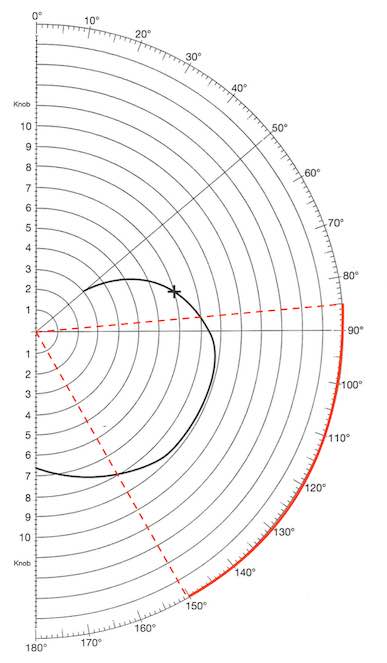
   Det ses, at intervallet er ca. 85 ° - 150°

Svar på opgave 3: Bygning af skibet

1. Stammen kløves i to, det er een kløvning. Hvert stykke kløves i to det vil sige, at to kløvninger mere giver fire stykker. Dette fortsættes og hver gang skal man kløve det antal stykker, som man er nået til.
   Man får i alt 1 + 2 + 4 + 8 + 16 = 31 gange
2. Nedenunder er vist et forslag i Geogebra, hvor målet viser størrelsen på papiret.
   
3. Kløvestykke (brunt) sammen med enden af brættet (gult) er tegnet nedenunder i Geogebra.
   
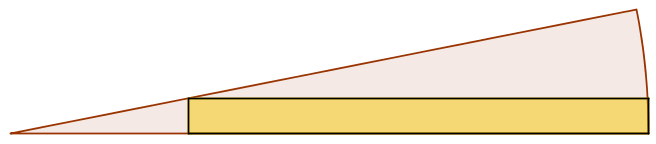
4. Man måler endestykkets bredde |AB| i Geogebra til 38,9 cm.
   

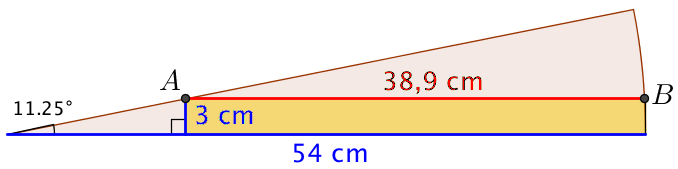
Svar på opgave 4: Ottars sejl

1. Sejlets vægt uden smørelse og tovværk er (243 - 113 - 45) kg = 85 kg
2. Sejlets styrke er (85.000 g)/(90 m²) = 944 g/m²
3. K = (1,2·438·9,82·0,21)/(1,52 + 0,21) = (1083,89/1,73) N = 627 N

Svar på opgave 5: Ottar

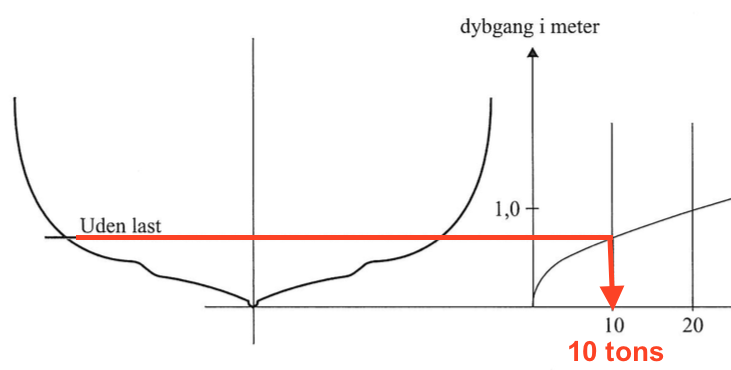
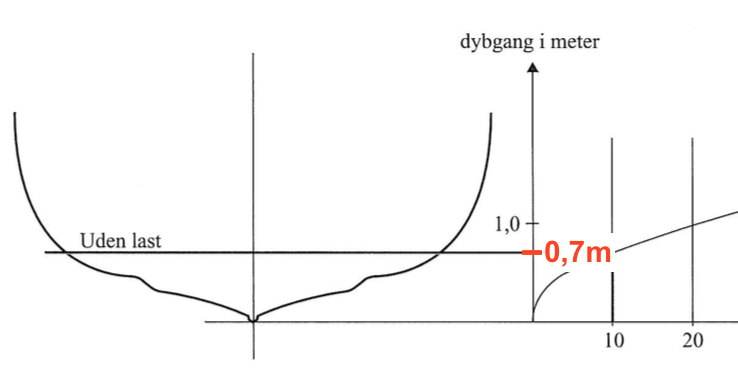
1. Skibets dybgang bliver uden last 0,7 m, hvilket aflæses af figuren som vist nedenunder.
   
2. Man får rumfanget (13/6)·(0,33 + 0,28 + 4·3,6) m² = 32,52 m²
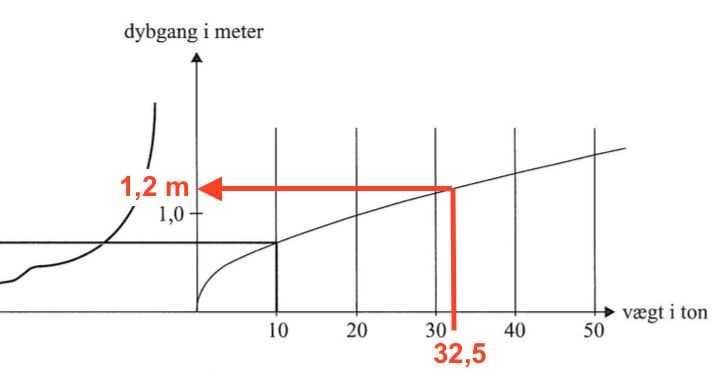
3. Dybgangen aflæses på svararket som vist nedenunder. Dybgangen er 1,2 m
   
4. Skibets vægt uden last aflæses af figuren øverst i opgaven til 10 tons som vist nedenunder. Lasten vejer: 32,5 tons - 10 tons = 22,5 tons