Svar på opgave 1 (liftkort og skileje):

1. Forskellen i pris for skileje i 6 og 7 dage er: 950 kr. - 880 kr. = 70 kr.
2. Den samlede pris for skileje og liftkort i 6 dage er: 1810 kr. + 880 kr. = 2690 kr.
3. Hun sparer: (2015 kr.)·(20 %) = 403 kr.

Svar på opgave 2 (valuta):

1. 100 svenske kr. = 80 danske kr. Dvs. 1 svensk kr. er 80/100 danske kr. = 0,80 danske kr.
   Dermed er 500 svenske kr. = 500·0,80 danske kr. = 400 danske kr.
2. 100 svenske kr. = 80 danske kr. Dvs. 1 dansk kr. er 100/80 svenske kr. = 1,25 svenske kr.
   Dermed er 120 danske kr. = 120·1,25 svenske kr. = 150 svenske kr.

Svar på opgave 3 (juice):

1. Anna skal betale 8·7,5 kr. = 60 kr.
2. Man omregner brikkens rumfang til L: 2,5 dL = 2,5·(1 dL) = 2,5·(0,1 L) = 0,25 L.
   Antal brikker er dermed: (3 L)/(0,25 L) = 3/0,25 stk. = 12 stk.

Svar på opgave 4 (taxa):

1. Anna skal betale: 40 kr. + (15 km)·(20 kr./km) = 340 kr.
2. Man kalder antallet af kørte km for x.
   Man får ligningen: 40 kr. + x·(20 kr./km) = 220 kr. ⇒
   x·(20 kr./km) = 220 kr. - 40 kr. ⇒
   x·(20 kr./km) = 180 kr. ⇒
   x = (180 kr.)/(20 kr./km) ⇒
   x = 9 km
   Dvs. taxaturen er på 9 km

Svar på opgave 5:

1. 919 + 12082 = 13001
2. 2039 - 150 = 1889
3. 90·102 = 9180
4. 8076:4 = 2019

Svar på opgave 6:

1. 15 - 5·4 = 15 - 20 = -5
2. 10 + 2·(3 - 4)² = 10 + 2·(-1)² = 10 + 2·1 = 12
3. 2⁴ = 2·2·2·2 = 16
4. √16 + √9 = 4 + 3 = 7
5. 6·(3/4) = 18/4 = 9/2 = 4,5 (eller 4½)

Svar på opgave 7:

1. Man kan tage gennemsnittet af de to tal, det ligger midt i mellem: (0,65 + 0,66)/2 = 0,655
2. (1/4)/2 = 1/(4·2) = 1/8
3. -0,6 + 5 = 5 - 0,6 = 4,4
4. 40 % af 550 kr. = 0,4·(550 kr.) = 0,4·550 kr. = 220 kr.
5. man kalder beløbet for x. Der gælder dermed ligningen: x·(75 %) = 225 kr. ⇒
   x·0,75 = 225 kr. ⇒
   x = (225 kr.)/0,75 ⇒
   x = 300 kr.
   Dvs. beløbet er 300 kr.

Svar på opgave 8 (is og cola):

1. Man kalder prisen for en cola for x og prisen for en is for y. Dette giver følgende to ligninger med to ubekendte:
   2·x + 2·y = 70 og 3·x + y = 75 ⇒
   x + y = 35 og 3·x + y = 75 ⇒
   y = 35 - x og y = 75 - 3·x ⇒
   35 - x = 75 - 3·x ⇒
   - x + 3· x = 75 - 35 ⇒
   2·x = 40 ⇒
   x = 40/2 ⇒
   x = 20
   Dvs. en cola koster 20 kr.

Svar på opgave 9:

1. 7·x - 12 = 37 ⇒
   7·x = 37 + 12 ⇒
   7·x = 49 ⇒
   x = 49/7 ⇒
   x = 7
2. x/5 = 15 ⇒
   x = 15·5 ⇒
   x = 75
   
3. 4·(x + 3) = 7·x + 3 ⇒
   4·x + 12 = 7·x + 3 ⇒
   4·x - 7·x = 3 - 12 ⇒
   -3·x = -9 ⇒
   x = (-9)/(-3) ⇒
   x = 9/3 ⇒
   x = 3

Svar på opgave 10 (cylinder):

1. Kryds ved V/(π·r²)

Svar på opgave 11 (fart):

1. Annas far løber 10 km på 1 time.
   15 minutter udgør 15/60 = 1/4 af en time.
   Dermed løber han (1/4)·(10 km) = 2,5 km på 15 minutter
2. Annas mor løber 9 km på 1 time, dvs. hun løber 1 km på 1/9 time.
   Dermed tager det hende: 1,5·(1/9 time) = 15/90 time = 1/6 time at løbe 1,5 km.
   1/6 time omregnes til minutter: (1/6) time = (1/6)·(1 time) = (1/6)·(60 min.) = 10 min.

Svar på opgave 12 (enheder):

1. 120 min = 120·(1 min) = 120·(1/60 time) = 120·(1/60) time = 2 timer
2. 1055 cm = 1055·(1 cm) = 1055·(0,01 m) = 1055·0,01 m = 10,55 m
3. 725 mm = 725·(1 mm) = 725·(0,1 cm) = 725·0,1 cm = 72,5 cm
4. 1 km² = 1·(1 km)² = 1·(1000 m)² = 1·1000² m² = 1.000.000 m²

Svar på opgave 13:

1. Vinkel D er den ene vinkel i firkant ADCE som vist nendeunder.
   
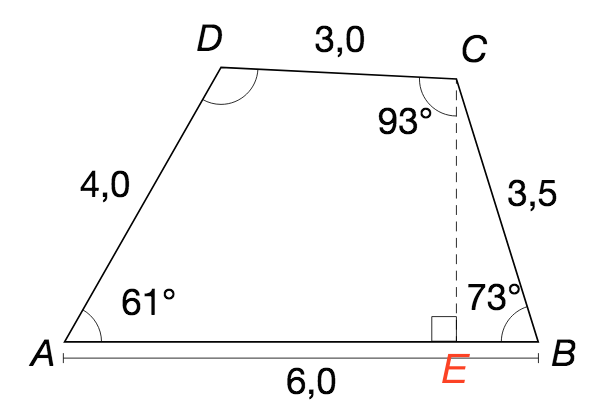
   Denne firkant har vinkelsummen 360°.
   De andre vinkler i firkanten er tilsammen: 61° + 93° + 90° = 244°.
   Dermed er vinkel D: 360° - 244° = 116°
2. Omkredsen er: 6,0 + 3,5 + 4,0 + 3,0 = 16,5

Svar på opgave 14:

1. Kryds ved figur 2 (en ligebenet trekant har højden som symmetriakse)

Svar på opgave 15 (kugle):

1. Kuglens diameter er 2·2 = 4
2. Kuglens rumfang er (4/3)·π·2³ = (4/3)·3·8 = 32
3. Kuglens overfladeareal er 4·π·2² = 4·3·4 = 48

Svar på opgave 16 (ligedannede trekanter):

1. Siden DE er ensliggende med BC, dvs. er omgivet af samme vinkler.
   Dermed er dens længde en tredjedel af BC: 12/3 = 4
2. Arealet er 3² = 9 gange større. (Længdeforholdet i anden)

Svar på opgave 17 (linje, koordinatsystem):

1. Kryds ved y = 2x + 3

Svar på opgave 18 (diagram):

1. Kryds ved ca. 50 % (Summen: 19,4 + 10,0 + 20,2)
2. Kryds ved ca. 100 % (Forholdet: (20,2-10)/10)

Svar på opgave 19 (median):

1. Middeltal: (1 + 1 + 4 + 7 + 5 + 5 + 5 + 2 + 1 + 4)/10 = 35/10 = 3,5
2. Median: man opstiller tallene i nummerorden og tager gennemsnittet af de to midterste:
   1, 1, 1, 2, 4, 4, 5, 5, 5, 7. Medianen er dermed: (4 + 4)/2 = 4
3. Størsteværdien ses at være 7

Svar på opgave 20 (lotteri):

1. Sandsynligheden er antallet af ens tal på de to plader divideret med 90.
   Dvs. sandsynligheden er (5/90)·100 % = 5,6 %
2. Sandsynligheden er antallet af forskellige tal, som ikke er på nogen af pladerne divideret med 90.
   Antallet af forskellige tal på de to plader er 2·15 - 5 = 25. (De 5 tal på den ene plade skal ikke tælles med)
   Antallet af forskellige tal, som ikke er på nogen af dem er: 90 - 25 = 65
   Sandsynligheden er dermed: (65/90)·100 % = 72,2 %