Svar på opgave 1: Antimon – en miljøgift i det antikke Rom

1. Der er tale om en redoxproces, fordi antimon stiger i oxidationstrin fra 0 (som Sb) til +3 (i SbO⁺), mens oxygen falder fra trin 0 (som O₂) til -2 (i H₂O).

2. Man kalder den formelle koncentration af Sb for C og koncentrationen af K₂Sb₂(C₄H₂O₆)₂ for C_salt.

   Der frigives 2 Sb-ioner hver gang, at en formelenhed af saltet opløses. Dette giver:

   C = 2·C_salt = 2·n_salt/V = 2·m_salt/(M_salt·V), hvor

   n_salt er stofmængden af saltet,

   m_salt er massen af saltet = 15,4·10^-3 g,

   M_salt er molmassen af saltet = 613,83 g/mol og

   V er opløsningens rumfang = 0,5 L.

   Dvs. den formelle koncentration af Sb er 2·(15,4·10^-3 g)/(613,83 g/mol·0,5 L) = 0,1 mM

3. Man skal finde masse-koncentrationen af Sb i vandfase (kaldet C-m_v). Fremgangsmåden er:

   1) Antag at stofmængden af Sb er den samme i vandfase som i organisk fase.

   2) Beregn stofmængde-koncentrationen af Sb i organisk fase ud fra absorbansen (A).

   3) Omregn stofmængde-koncentration til masse-koncentration.

   I det følgende henviser indeks v til vandfase og indeks o til organisk fase. C er stofmængde-

   koncentration af Sb, n er stofmængde af Sb, M er molmasse af Sb og V er rumfang af væskefase.

   Angående 1): n_v = n_o ⇒ C_v·V_v = C_o·V_o ⇒ C_v = C_o·V_o/V_v.

   Angående 2): A = 73,671·C_o + 0,001 ⇒ C_o = (A - 0,001)/73,671.

                1+2): C_v = C_o·V_o/V_v = ((A - 0,001)/73,671 mmol/L)·V_o/V_v.

   Angående 3): C-m_v = M·C_v = M·((A - 0,001)/73,671 mmol/L)·V_o/V_v. Tallene indsættes:

   C-m_v = (121,76 g/mol)·((0,573 - 0,001)/73,671 mmol/L)·(0,010 L)/(0,250 L) = 0,0378 mg/L

Svar på opgave 2: Wolfram i elektroniske komponenter

1. K = (p_HF)⁶/[(p_WF6)·(p_H2)³]. Partialtrykket måles i bar. Derfor bliver den samlede enhed for K:

   bar⁶/(bar·bar³) = bar^6-1-3 = bar²

2. For reaktionens ændring i molær entropi gælder der: ΔS^⊖(reaktion) = ΔS^⊖(W(s)) + 6·ΔS^⊖(HF(g)) - [ΔS^⊖(WF₆(g)) + 3·ΔS^⊖(H₂(g))], hvor

   ΔS^⊖(WF₆(g)) = molær dannelsesentropi for WF₆(g) = 354 J/(mol·K)

   ΔS^⊖(H₂(g)) = molær dannelsesentropi for H₂(g) = 130,68 J/(mol·K)

   ΔS^⊖(W(s)) = molær dannelsesentropi for W(s) = 32,68 J/(mol·K)

   ΔS^⊖(HF(g)) = molær dannelsesentropi for HF(g) = 173,8 J/(mol·K).

   Man får: ΔS^⊖(reaktion) = (32,68 + 6·173,8 - (354 + 3·130,68)) J/(mol·K) = 329,4 J/(mol·K)

   Kommentar: entropiændringen er positiv, dvs. entropien vokser, hvilket passer med, at der bliver flere gasmolekyler ved reaktionen.

3. Der gælder: K_eq = exp(-ΔG^⊖/(R·T)), hvor

   ΔG^⊖ = ΔH^⊖ - T·ΔS^⊖

   Det antages, at ΔH^⊖ og ΔS^⊖ er uafhængige af temperaturen. Det antages også, at reaktionsblandingen er en ideal gas, hvorved K_eq er uafhængig af totaltrykket.

   Ændringen i molær enthalpi for reaktionen findes på samme måde som entropiændringen.

   ΔH^⊖(WF₆(g)) = -273,3 kJ/mol

   ΔH^⊖(H₂(g)) = 0

   ΔH^⊖(W(s)) = 0

   ΔH^⊖(HF(g)) = -1721,5 kJ/mol

   ΔH^⊖(reaktion) = (0 + 6·(-273,2) - (-1721,5 + 3·0)) kJ/mol = 81,7 kJ/mol.

   ΔG^⊖ = 81,7 kJ/mol - ((273,15 + 300) K)·(329,4 J/(mol·K)) = −107119 J/mol

   K_eq = exp(107119/(8,314·573,15)) bar² = 5,79·10⁹ bar²

4. Y = (0,0011 bar)⁶/[(0,0018 bar)·(0,0439 bar)³] = 1,16·10^-11 bar²

   Da Y < K_eq, så vil reaktionen forløbe mod højre og W udfældes.

Svar på opgave 3: Galanthamin – et middel mod mild Alzheimer

1. Affarvningen af Br₂-vand skyldes en additionsproces. Br adderes til den alifatiske C=C dobbeltbinding (en alken), så den bliver en enkeltbinding. Dette er vist nedenunder.

   

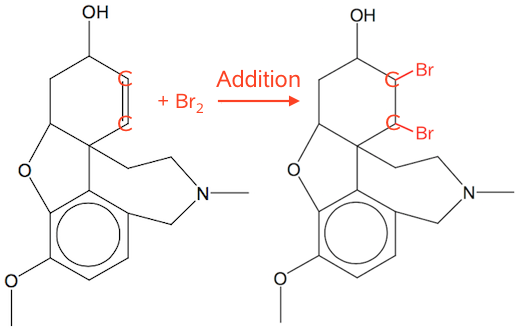
2. Reaktionstyperne er (1): elektrofil substitution eller aromatisk halogenation. H erstattes af Br på benzenring som vist nedenunder:

   

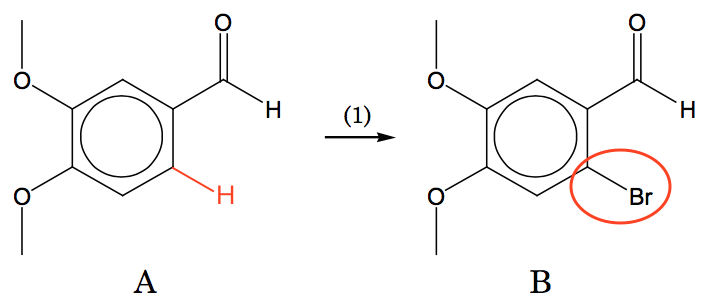
   Denne reaktion forløber ikke så let som addition af Br til alifatisk dobbeltbinding. Som katalysator bruges en Lewis syre som f.eks. AlCl₃.

   (4): Reduktion eller redoxproces. C bundet til O reduceres fra +2 (i C=O) til +1 (i C-OH). Dette er vist nedenunder:

   

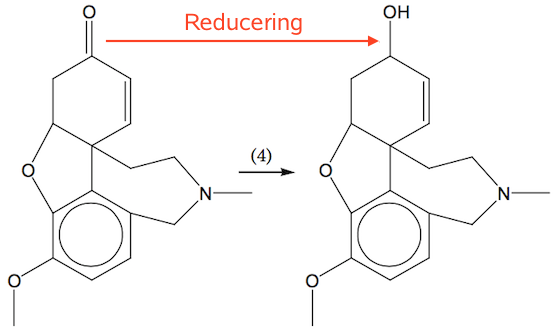
   Som reduktionsmiddel bruges f.eks. LiAlH₄.

3. Galanthamin er en tertiær amin med en amingruppe og dermed en monoprot organisk base.

   pK_b = -log(9,33·10^-7) = 6,03. Der er tale om en svag base, da 4 < pK_b < 10.

   Formlen for pH af en svag monoprot base er: pH = 14 - 0,5·(pK_b - log(C_b)).

   Man finder den formelle koncentration (C_b) af basen:

   C_b = (1,7 g/L)/(287,36 g/mol) = 0,00592 mol/L. Dette giver følgende for opløsningens surhedsgrad:

   pH = 14 - 0,5·[6,03 - log(0,00592)] = 9,9

4. IR: A og C vil have et bånd ved 1700 cm^-1 for C = O strækning samt et bånd ved 2800 cm^-1 på grund af (C=O) - H strækning.

   C og galanthamin vil have et bredt bånd ved 3300 cm^-1 på grund af C-O - H strækning.

   D og galanthamin vil have et bånd ved 1600 cm^-1 på grund af C = C strækning i alken.

   D vil have et bånd ved 1700 cm^-1 for C = O strækning, men mangler båndet ved 2800 cm^-1 for (C=O) - H strækning.

   NMR: De H-atomer, der sidder på benzenringene vil give en top (eller flere sammensmeltede toppe) med et kemisk skift omkring 7 (kan ikke forveksles med H bundet til andre grupper). For A vil disse toppe have et integral på 3 H, mens de på B vil have et integral på 2 H.

5. På figuren nedenunder er hydrofobe interaktioner vist med røde pile, mens brintbindinger mellem polære grupper er vist med blå.

   

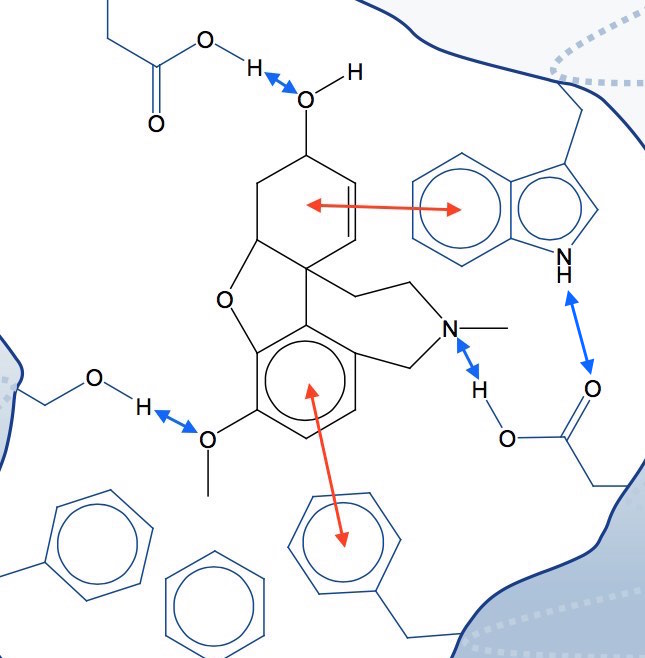
   De forkellige gruppers placering i enzymet ses at matche placingerne af tilsvarende grupper i molekylet, så dette kan passes ind på det viste sted i enzymet.

Svar på opgave 4: Tramadol – et morfinlignende stof

1. Nedenunder er C og H atomer vist med rødt. H-atomer er vist med streger.

   

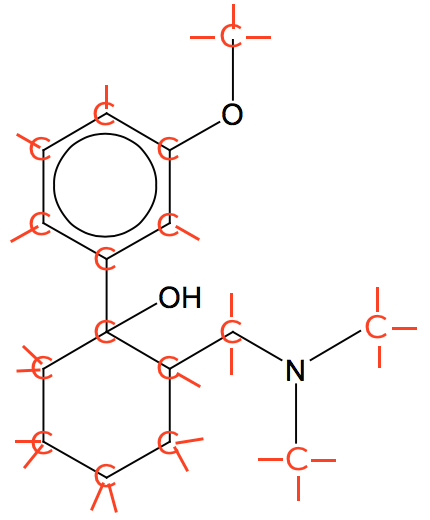
2. Nedenunder er reaktionsskemaet vist. Det andet produkt er methylbromid.

   

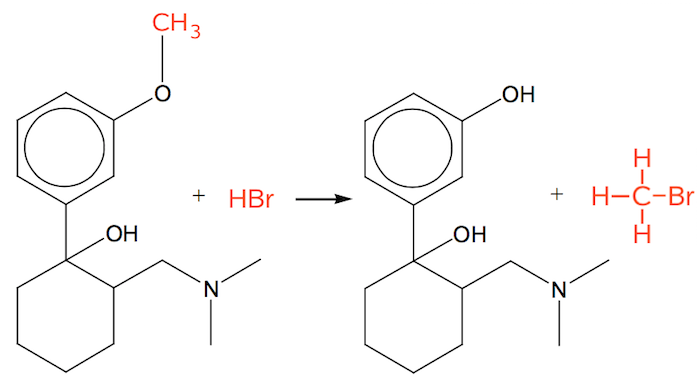
   Reaktionen er en nukleofil susbstitution (sur kløvning af æter).

3. Der gælder følgende for reaktionsordenen med hensyn til koncentrationen (C) af et stof i en reaktion:

   Hvis man afbilder C mod tiden, så vil grafen være en ret linje, når reaktionen er af nulte orden.

   Hvis man afbilder ln(C) mod tiden, så vil grafen være en ret linje, når reaktionen er af første orden.

   Hvis man afbilder 1/C mod tiden, så vil grafen være en ret linje, når reaktionen er af anden orden.

   For at analysere forløbet af C, så laver man alle de tre ovennævnte grafer. Disse kan dels bruges til at finde reaktionsordenen, dels til at afgøre, hvor længe tramadol er om at blive optaget i kroppen.

   Man opretter lister med tid og C (c_tramadol) i Ti-Nspire.

   tid:={10,30,50,70,90,200,350,480,600} ▸ {10,30,50,70,90,200,350,480,600}

   c_tramadol:={21.,3.,1.5,1.1,0.81,0.46,0.23,0.14,0.072} ▸ {21.,3.,1.5,1.1,0.81,0.46,0.23,0.14,0.072}

   Man afbilder C som funktion af tiden (de sidste syv punkter vist):

   

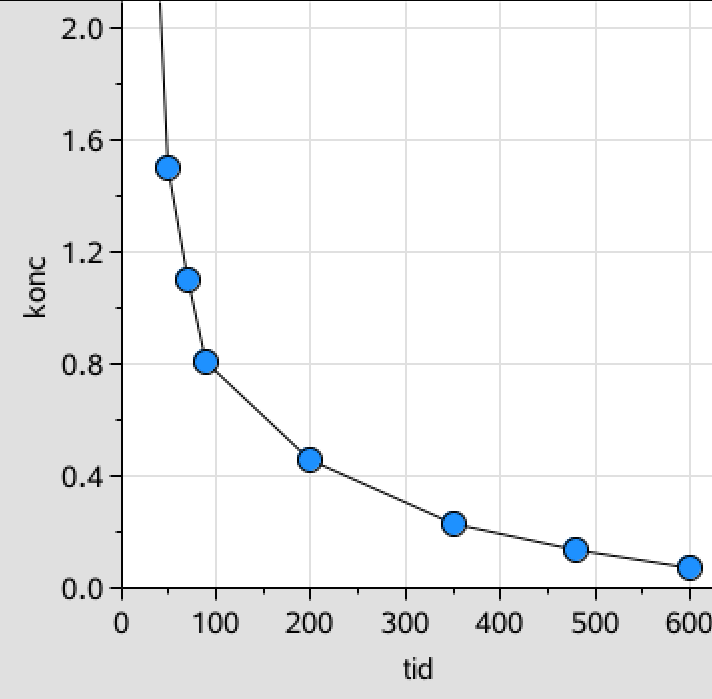
   Punkterne ser ikke ud til at ligge på en ret linje. Dette tyder på, at reaktionen ikke er nulte ordens.

   Man opretter derefter en liste med den naturlige logaritme til C og afbilder denne mod t:

   ln_c_tramadol:=ln(c_tramadol) ▸ {3.04452,1.09861,0.405465,0.09531,−0.210721,−0.776529,−1.46968,−1.96611,−2.63109}

   

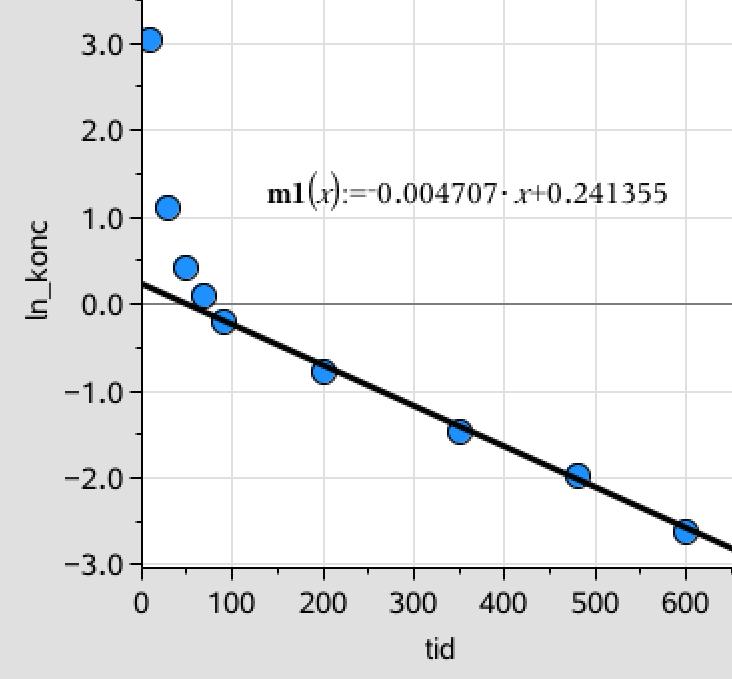
   Her nærmer kurven sig en ret linje på de sidste fem punkter, hvilket tyder på, at reaktionen er af første orden med hensyn til C efter ca. 100 minutter.

   For at undersøge for anden orden, så laver en liste over den reciprokke til C kaldet rec_c_tramadol:

   rec_c_tramadol:=1/c_tramadol ▸ {0.04762,0.33333,0.66667,0.90909,1.2346,2.1739,4.3478,7.1429,13.889}

   Disse værdier afbildes som funktion af tiden:

   

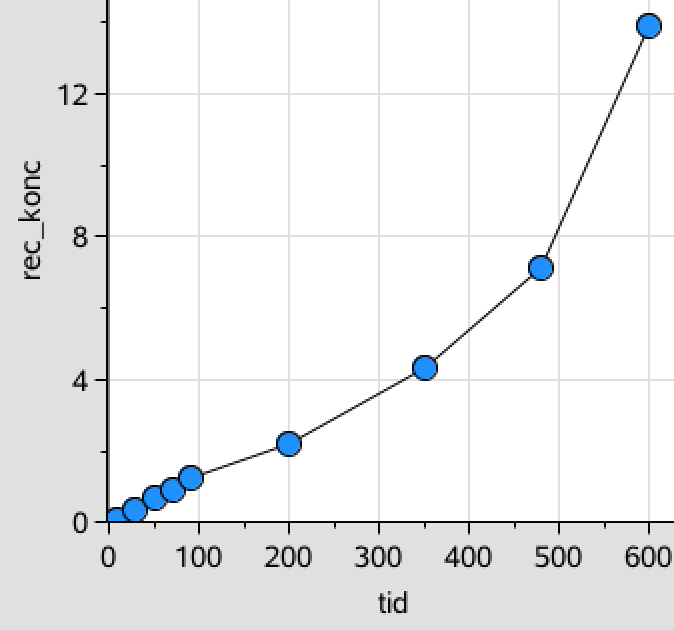
   Her ser det ud til, at den første periode (før 100 min.) følger en ret linje og dermed er anden-ordens. Den anden del (efter 100 min.), som er den man er spurgt om, følger derimod ikke en ret linje.

   Konklusionen er derfor, at tramadol optages i kroppen i løbet af de første 100 minutter. I denne periode følger koncentrationen af tramadol en andenordens reaktion. Efter optagelsen i kroppen (fra ca. 100 minutter), så følger koncentrationen en første ordens reaktion

   Af den anden af de ovenstående grafer ses, at Koncentrationen af tramadol følger formlen:

   ln(C) = 0,0047·t + 0,24, hvilket giver: C = e^{0,0047·t + 0,24} = 1,27·e^0,0047·t

4. Der tænkes nok på adskillelse af stoffet D og L-vinsyre ved optagelse i hver sin fase. Adskillelsen afhænger af stoffernes polaritet, og om de er på ionform.

   Polaritet: D har 15 C-atomer og 3 polære grupper, dvs. 5 C for hver polære gruppe. Dermed er det mindre polært end L-vinsyre, der har 4 C-tomer og 4 polære grupper (2 -OH og 2 -COOH).

   Ionform: D er en base og optager et H⁺ i surt miljø. D er dog ikke på ionform ved pH 12, idet pH er ca. 3 enheder over pK_b for D.

   Vinsyre derimod er på ionform, da det er en carboxyl-syre og den vandige opløsning er basisk. Nedenunder er vist de ladninger, som stofferne har i saltet F.

   

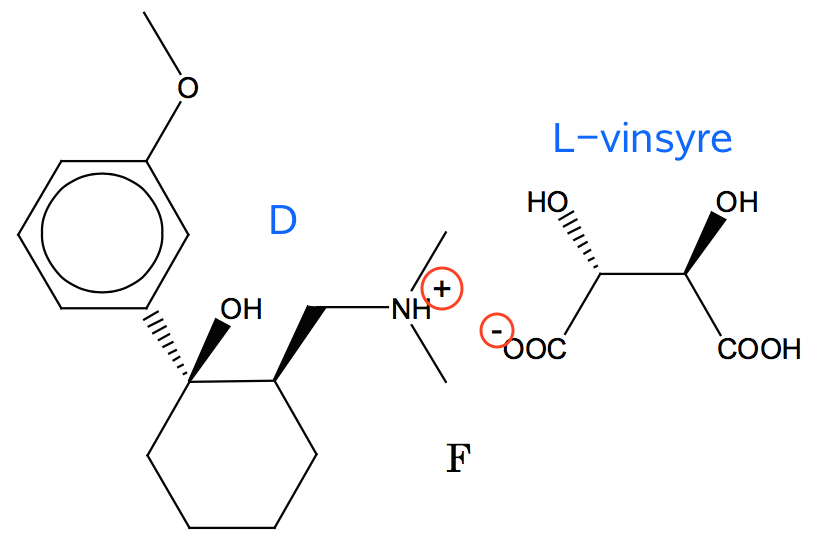
   Da D er relativt upolært og uladet (dvs. ikke på ionform) ved pH 12, så vil det i højere grad findes i den organiske fase end L-vinsyre, der er mere polært end D og desuden på ionform ved pH 12.

   På den måde kan D og L-vinsyre adskilles ved hjælp af en vandfase og en organisk fase.