Svar på opgave 1: Feromoner

1. Br₂ adderes til den alifatiske C=C dobbeltbinding som vist nedenunder:

   

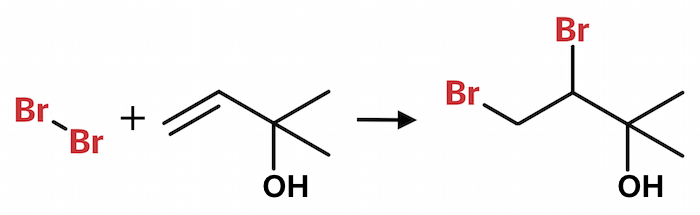
   Derved forsvinder farven, der skyldes Br₂.

2. Molekylet har den generelle molekyleformel:

   C_xH_yO₂.

   Man ved, at der indgår 2 oxygenatomer i molekylet, da alkyl ikke indeholder oxygen. Man skal finde stoffets molmasse, M, og bruger oplysningen om masseprocenten for oxygen i molekylet:

   2·M_O/M = 31,33 % ⇒ M = 2·M_O/0,3133 = 2·(16,00 g/mol)/0,3133 = 102,1 g/mol.
   Her er M_O = molmassen for oxygen = 16,00 g/mol.

   Man har desuden, at molmassen af carbon = M_C = 12,01 g/mol og molmassen af hydrogen = M_H = 1,01 g/mol.

   Dette benyttes til at finde x og y, idet der gælder:

   x·M_C/M = 58,82 % ⇒ x = 0,5882·M/M_C = 0,5882·(102,1 g/mol)/(12,01 g/mol) = 5,00

   y·M_H/M = 9,87 % ⇒ y = 0,0987·M/M_H = 0,0987·(102,1 g/mol)/(1,01 g/mol) = 10,1.

   Dette giver den færdige molekyleformel:

   C₅H₁₀O₂

3. Nedenunder er vist to isomerer. Den til venstre er pentansyre og den til højre er 2-methyl­butansyre.

   

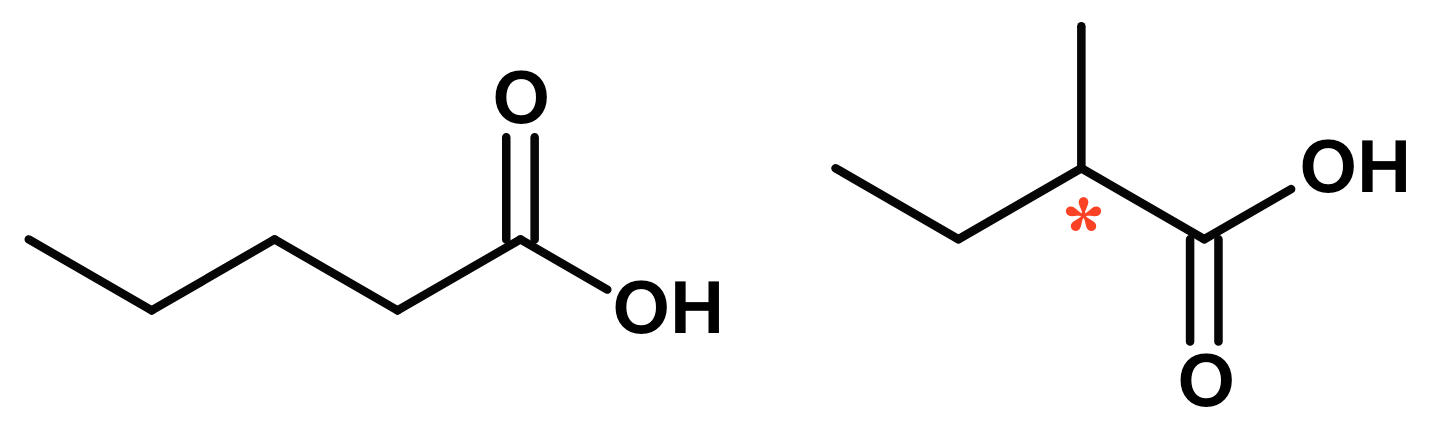
   2-methylbutansyre er optisk aktiv fordi, den har et asymmetrisk carbonatom, som er markeret med en stjerne.

   Navngivning af 2-methylbutansyre: Den funktionelle gruppe, som har højest prioritet er carboxyl­syre (-COOH). Den længste kæde, som indeholder denne gruppe er butansyre. Denne kæde har en substituent, som er methyl på plads nummer 2 i kæden, idet man regner C'et i COOH for nummer 1.

4. Der er følgende muligheder:

   

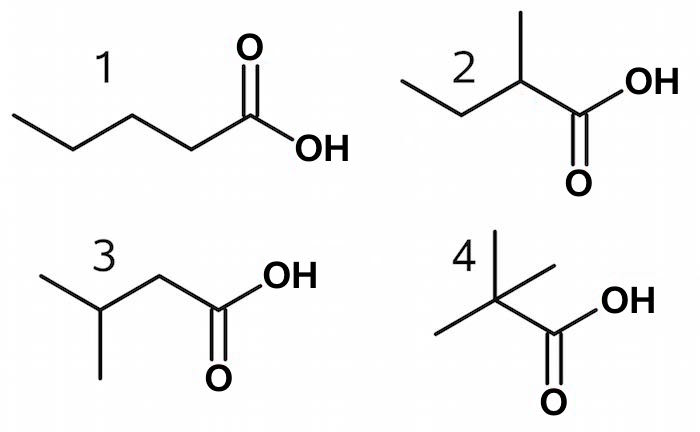
   Man kan udelukke mulighederne 2-4, fordi de har mere end en CH₃-gruppe, og dermed ville de give mere end en top med integralet der svarer til 3 H, eller de ville give en top et integral, der svarer til 6 H eller 9 H.

   Det rigtige stof er dermed pentansyre, som er eftervist nedenunder:

   

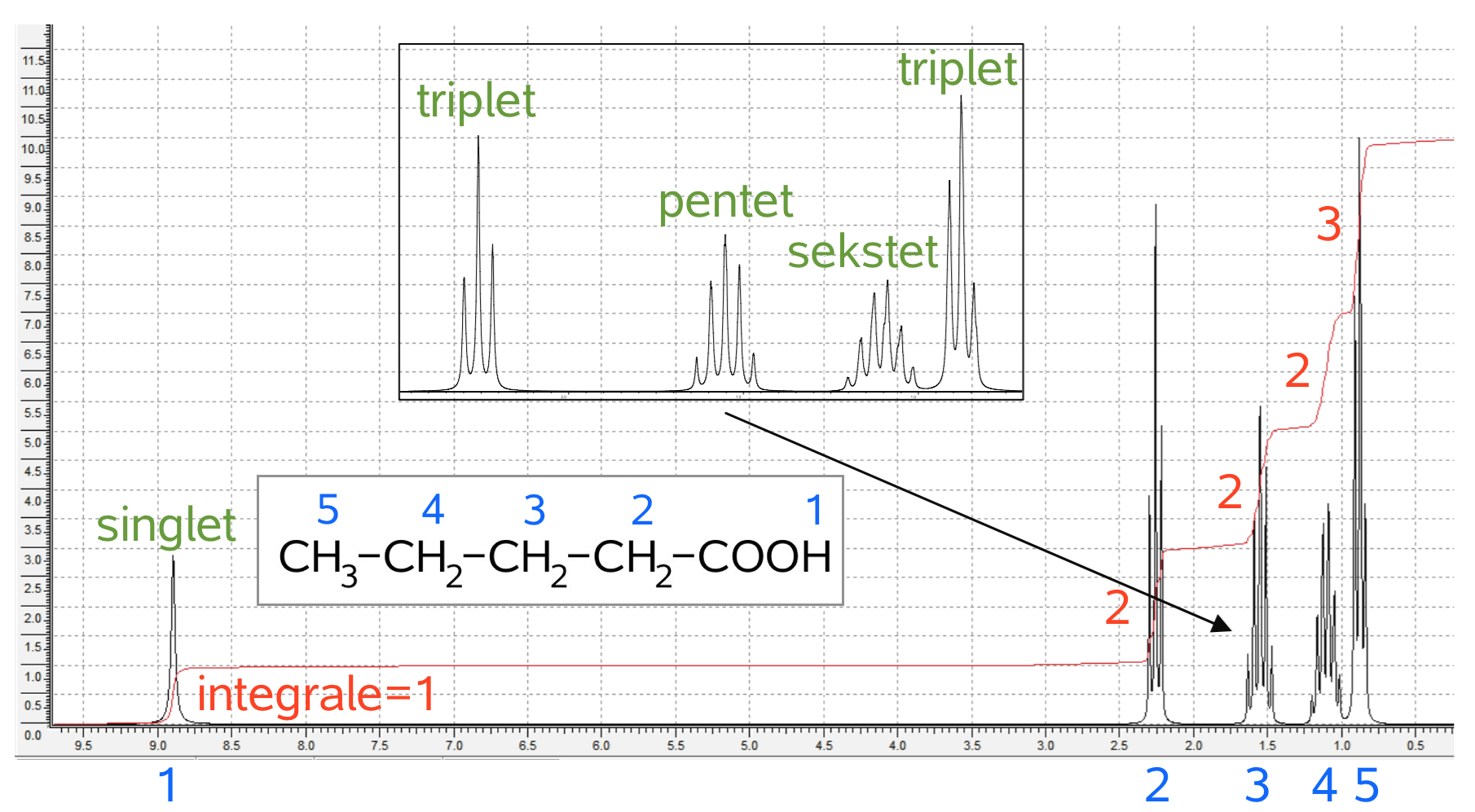
   Blå tal angiver placeringen i molekylet af de H'er, der ingår en top. Røde tal er integrale pr. top.

   1. Det H, der indgår i COOH, giver en singlet (1 tak), da det er bundet til O og dermed ikke kobler med andre H. Den har et integral på 1 og dermed ved man, at integral svarer til antal H i en top. Toppen har et højt kemisk skift på ca. 9, hvilket passer med at den sidder i en carboxylsyregruppe, hvor de to O'er deshielder H'et.

   2. Integral = 2 H, hvilket passer med CH₂. Splittet (eller koblingsmønstret) er en triplet (3 takker) hvilket passer med de to H'er, der sidder på C'er, der kommer efter COOH. Disse to H'er har to H'er som naboer på de nærmeste C'er, og dermed giver splittet en triplet (i følge reglen n + 1, hvor n er antal nabo H'er). Det kemiske skift er ikke højt, men stadig det næsthøjeste for en top, hvilket passer med, at de to H'er i toppen er dem, som er næsttættest på O'erne.

   3. Integral = 2 H, hvilket passer med CH₂. Split = pentet (5 takker), hvilket passer med 4 nabo H'er. Skiftet er mindre end top nr. 2, hvilket passer med større afstand til O'erne.

   4. Integral = 2 H, hvilket passer med CH₂. Split = sekstet (6 takker), hvilket passer med 5 nabo H'er. Skiftet er mindre end top nr. 3, hvilket passer med større afstand til O'erne.

   5. Integral = 3 H, hvilket passer med CH₃. Split = triplet, hvilket passer med 2 nabo H'er. Skiftet er mindst, hvilket passer med størst afstand til O'erne.

Svar på opgave 2: Fremstilling af jern

1. Det er en redox-reaktion, fordi Fe går fra oxidationstrin +3 i Fe₂O₃ til oxidationstrin 0 i Fe. Imens går H fra oxidationstrin 0 i H₂ til oxidationstrin +1 i H₂O.

2. ΔH^⊖ (den molære standard-enthalpi for reaktionen) for reaktionen beregnes ud fra de indgående stoffers molære dannelses-enthalpier. Man tager summen af dannelses-enthalpierne for produkterne vægtet med reaktions-ligningens koefficienter og trækker fra dette den vægtede sum af dannelses-enthalpierne for reaktanterne.

   Man får ifølge tabel følgende dannelses-enthalpier:

      ΔH^⊖(Fe₂O₃(s)) = -824,2 kJ/mol

      ΔH^⊖(H₂(g)) = 0 (naturligt forekommende form i grundtilstanden)

      ΔH^⊖(Fe(s)) = 0 (naturligt forekommende form i grundtilstanden)

      ΔH^⊖(H₂O(g)) = -241,8 kJ/mol

   Dette giver: ΔH^⊖ = 3·(-241,8 kJ/mol) - (-824,2 kJ/mol) = 98,8 kJ/mol

   Kommentar: reaktionen er endoterm, da ΔH^⊖ > 0. Dvs. der bruges varme, når reaktionen forløber mod højre.

3. Man skal bruge formlen for den molære frie Gibbs energi for reaktionen:

   ΔG^⊖ = ΔH^⊖ - T·ΔS^⊖

   Her er T den temperatur, som reaktionen foregår ved, mål i Kelvin. Reaktionen forløber spontant mod højre i grundtilstanden, når ΔG^⊖ < 0. Man skal derfor lave en fortegnsundersøgelse for ΔG^⊖.

   Først bestemmes ΔS^⊖. Man får ifølge tabellen følgende dannelses-entropier:

      ΔS^⊖(Fe₂O₃(s)) = 87,4 J/mol

      ΔS^⊖(H₂(g)) = 130,68 J/mol

      ΔS^⊖(Fe(s)) = 27,3 J/mol

      ΔS^⊖(H₂O(g)) = 188,8 J/mol

   Dette giver: ΔS^⊖ = 2·(27,3 J/(mol·K)) + 3·(188,8 J/(mol·K)) - 87,4 J/(mol·K)) - 3·(130,68 J/(mol·K)) = 141,56 J/(mol·K).

   Man får dermed: ΔG^⊖ = 98,8·10³ J/mol - T·(1,42·10² J/(mol·K))

   ΔG^⊖ = 0 ⇒ 98,8·10³ J/mol - T·(1,42·10² J/(mol·K)) = 0 ⇒ T = 698 K

   For T > 698 K så vil ΔG^⊖ være negativ og dermed er 698 K den laveste temperatur, hvorved reaktionen vil forløbe spontant (mod højre).

4. Man skal finde reaktionsbrøken, Y, for reaktionen ved 800 K og sammenligne den med ligevægstkonstanten, K = 8,79, for at vurdere hvilken vej reaktionen vil forløbe.

   Man får: Y = (p(H₂O)/p(H₂))³ = (0,5/0,45)³ = 1,4.

   Da Y < K, så vil reaktionen forløbe mod højre for at komme i ligevægt.

   Dette skyldes, at på denne måde vil tælleren i Y øges samtidig med, at nævneren bliver mindre, og Y vil dermed blive større.

5. Da H₂ og H₂O har sammen koefficienten i reaktionsskemaet (3), så vil det sige, at hver gang, der forsvinder Δn mol H₂, så vil der dannes Δn mol H₂O (stofferne reagerer 1:1).

   Da de to stoffer befinder sig i en lukket beholder, vil det sige, at hver gang partialtrykket af H₂ mindskes med Δp, så vil partialtrykket af H₂O øges med Δp.

   Ligevægtstrykket for H₂ er dermed 0,45 bar - Δp og ligevægtstrykket for H₂O er 0,50 bar + Δp.

   Man har dermed følgende ligning for Δp:

   ((0,50 bar + Δp)/(0,45 bar - Δp))³ = 8,79 ⇒ Δp = 0,14 bar

   Dermed er

      ligevægtstrykket for H₂ lig med 0,45 bar - 0,14 bar = 0,31 bar og

      ligevægtstrykket for H₂O lig med 0,50 bar + 0,14 bar = 0,64 bar

   Man kan også sige, at for reaktionen:
      Fe₂O₃ (s) + 3 H₂ (g) → 2 Fe (s) + 3 H₂O (g)
   er der lige mange formelenheder af gasformige stoffer på begge sider af reaktionsligningen, og derfor vil den samlede stofmængde af gas ikke ændres og totaltrykket, p, være konstant under reaktionen. (Forudsat idealgas-loven gælder).
   Dermed gælder, at p(H₂) + p(H₂O) = 0,50 + 0,45 = 0,95 fra start til ligevægt.
   Man kan så sætte p(H₂O) = 0,95 - p(H₂) og man får følgende ligning for p(H₂) ved ligevægt:
   ((0,95 bar - p(H₂))/p(H₂))³ = 8,79 ⇒ p(H₂) = 0,31 bar, og p(H₂O) = (0,95 - 0,31) bar = 0,64 bar.

Svar på opgave 3: Nedbrydning af et kunstigt sødemiddel

1. Man bruger formlerne C = n/V = m/(M·V) ⇒ m = C·M·V, hvor

      C er stofmængdekoncentrationen af aspartam,

      n er stofmængden af aspartam,

      M er molmassen af aspartam og

      V er opløsningens rumfang.

   Man får m = (1,78·10^-3 mol/L)·(294,3 g/mol)·(250·10^-3 L) = 0,131 g

   Dvs. der skal afvejes 0,131 g = 131 mg aspartam.

2. Man har, at Citrat er en svag base. Det ses af, at pK_b > 4.

   Man bruger formlen for pH i svag base: pH = 14 - pOH = 14 - 0,5·(pK_b - log(C_b)). Dette giver:

   pH = 14 - 0,5·(7,6 - log(0,2)) = 9,85 i opløsning A.

3. Man opretter lister for tid (tid), koncentration af aspartam (konc) og den naturlige logaritme til koncentrationen af aspartam (lnkonc).

   tid:={0,30,90,150,210,270,330} ▸ {0,30,90,150,210,270,330}

   konc:={1.78,1.64,1.38,1.22,0.989,0.836,0.707} ▸ {1.78,1.64,1.38,1.22,0.989,0.836,0.707}

   lnkonc:=ln(konc) ▸ {0.576613,0.494696,0.322083,0.198851,−0.011061,−0.179127,−0.346725}

   Man laver et plot af den naturlige logaritme til koncentrationen mod tiden for aspartam. Denne ses at give en ret linje:

   

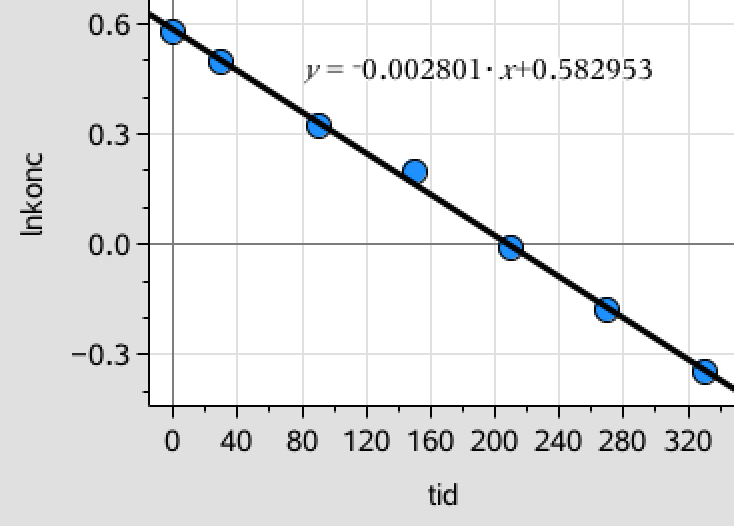
   Dette viser, at reaktionen er af første orden med hensyn til koncentrationen af aspartam.

   Sammenhængen ses at være ln([aspartam]) = -0,00280·t + 0,583 ⇒ [aspartam](t) = 1,791·exp(-0,00280·t).

   Man skal finde halveringstiden, T_1/2, og vælger at se på halveringen af [aspartam](0), dvs. koncentrationen af aspartam fra t = 0. (Starttidspunktet er underordnet for en førsteordens reaktion).

   [aspartam](T_1/2) = 0,5·[aspartam](0) ⇒

   1,791·exp(-0,00280·T_1/2) = 0,5·1,791·exp(0) ⇒

   T_1/2 = ln(0,5)/(-0,00280) = 247

   Dvs. der går 247 min. før koncentrationen af aspartam er halveret.

4. Man skal finde molbrøken af Cit^3- som er y(Cit^3-) = [Cit^3-]/([H₃Cit] + [H₂Cit^-] + [HCit^2-] + [Cit^3-])

   Den grønne kurve viser syrebrøken for HCit^2-: x_S(HCit^2-) = [HCit^2-]/([HCit^2-] + [Cit^3-]).

   Tilsvarende kan man aflæse basebrøken til Cit^3-: x_B(Cit^2-) = 1 - x_S(HCit^2-) = [Cit^3-]/([HCit^2-] + [Cit^3-]).

   Af bjerrumdiagrammet aflæses at x_B(Cit^3-) = [Cit^3-]/([HCit^2-] + [Cit^3-]) = 1 - 0,2 = 0,8, som vist:

   

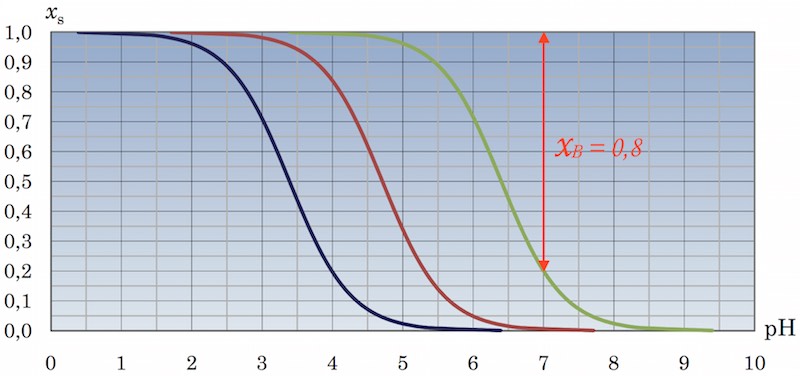
   Molbrøken for Cit^3- er dermed ca. 0,8, idet [H₃Cit] og [H₂Cit^-] er ca. lig med 0 og dermed molbrøken for citrat ca. lig med dens basebrøk.

   Dvs. andelen af Cit^3- er 80 %

5. I følge pufferligningen (eller Henderson-Hasselbalch-ligningen) har man:

   pH = pK_s + log(n_b/n_s) = 14 - pK_b + log(n_b/n_s). Her er n_b lig med stofmængden af Cit^3- og n_s er stofmængden af HCit^2-.

   Når pH 7,0 er nået, så skal der gælde: 7,0 = 14 - 7,6 + log(n_b/n_s) ⇒ 0,60 = log(n_b/n_s) ⇒ 10^0,60 = n_b/n_s ⇒ n_b/n_s = 3,98.

   Der gælder ifølge reaktionsskemaet, at n_s = n_s,start + n_HCl og n_b = n_b,start - n_HCl, hvor n_b,start og n_s,start er start-stofmængderne af henholdsvis citrat og dens korresponderende syre.

   Da citrat er en svag base antages, at n_s,start = 0.

   Samtidig er n_b,start = C_b·V_p = (0,200 mol/L)·(0,250 L) = 0,05 mol. Her er C_b den formelle koncentration af citrat i opløsning A fra start og V_p er pufferens rumfang.

   Man kan nu finde n_HCl, den tilsatte stofmængde af HCl: n_b/n_s = 3,98 ⇒ (n_b,start - n_HCl)/(n_s,start + n_HCl) = 3,98 ⇒ (0,05 mol - n_HCl)/n_HCl = 3,98 ⇒ n_HCl = 0,0100 mol

   Heraf fås det tilsatte rumfang af HCl-opløsning, idet der gælder, at n_HCL = V_HCl·C_HCL ⇒ V_HCl = n_HCL/C_HCL = (0,010 mol)·(1 M) = 0,01 L = 10 mL.

   Dvs. der skal tilsættes 10 mL 1 M HCl-opløsning for at indstille pufferopløsning A til en pH på 7.

Svar på opgave 4: Phenylhydraziner i champignon

1. Man tilføjer C'erne og de manglende H'er til stregformlen for agaritin.

   

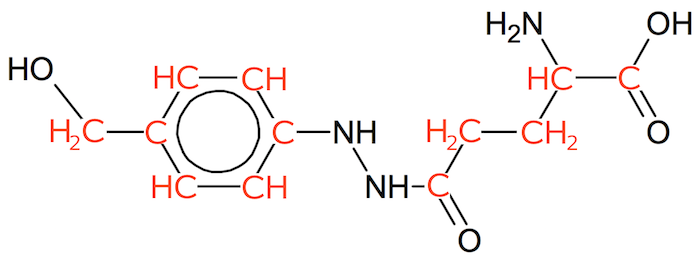
   Det ses, at der er 12 C, 17H, 3N og 4O. Dermed er molekyleformlen for agaritin:

   C₁₂H₁₇N₃O₄

   (I molekyleformler for organiske stoffer starter man med C og H, hvorpå følger de andre grundstoffer i alfabetisk orden).

2. Aldehyd-gruppen i A reduceres til en alkohol-gruppe i agaritin. Dette er vist nedenfor:

   

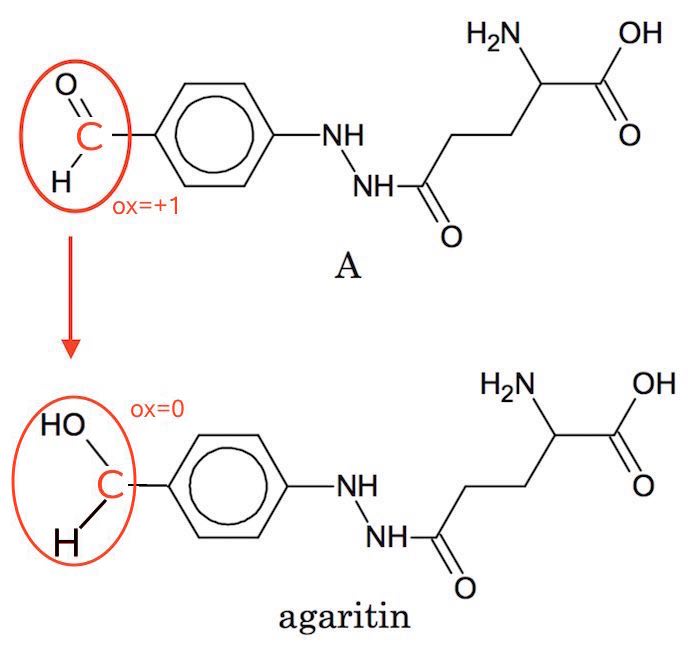
   Oxidationstrinnet for det C, der er bundet til O, går fra +1 i aldehyden til 0 i alkoholen.

   Dvs. der er tale om en redoxproces

3. Agaritin har 6 hydrofile grupper, som er markeret med røde ringe på figuren nedenunder.

   

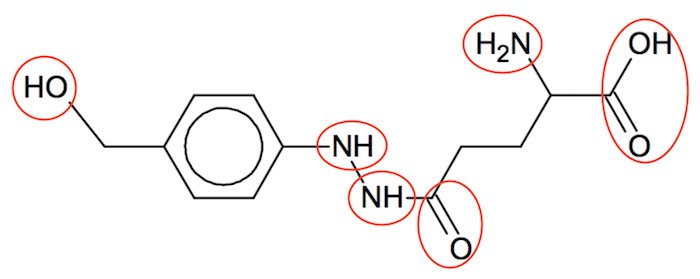
   Samtidig indeholder agaritin 12 carbonatomer.

   Regler er, at hvis der er 4 C-atomer eller mindre for hver hydrofil gruppe, så er et organisk stof vandopløseligt. Da agaritin har to C-atomer for hver hydrofil gruppe, så er det vandopløseligt.

   Dvs. vand er bedre end heptan som opløsningsmiddel til agaritin.

4. Man kalder massen af agaritin i 1 kg champion for m_a,kg.

   I 100 mg champion er massen af agaritin lig med 0,100·m_a,kg.

   I 100 mL ekstrakt er der også 0,100·m_a,kg agaritin, idet det antages, at alt agaritin kommer med i ekstraktet.

   I 25 μL af ekstraktet er der (0,100·m_a,kg)·(25·10^-6 L)/(0,100 L) = 2,5·10^-5·m_a,kg

   Af figur 2 fremgår det, at: y = 3,48·10⁵·x + 2,04·10⁴, hvor y er arealtallet, og x er antal ng af agaritin i prøven på 25 μL.

   Man ved, at arealtallet for prøven på 25 μL er 1,23·10⁶ og løser den fremkomne ligning med hensyn til x:

   1,23·10⁶ = 3,48·10⁵·x + 2,04·10⁴ ⇒ x = 3,48.

   Dvs. i prøven på 25 μL er der 3,48 ng agaritin. Dette giver følgende ligning med hensyn til m_a,kg: 2,5·10^-5·m_a,kg = 3,48 ng ⇒ m_a,kg = (3,48·10^-9 g)/(2,5·10^-5) = 0,139 g.

   Dvs. i 1 kg champion er der 139 mg agaritin.