
Svar på opgave 1: Elektrisk skotørrer
-
Der gælder formlen: P = U·I, hvor
P er effekten i varmelegemet,
U er spændingsforskellen over varmelegemet og
I er strømstyrken gennem det.
Man får for strømstyrken: I = P/U = (4,0 W)/(230 V) = 17 mA
-
Man er nød til at gøre nogle antagelser for at forenkle problemet.
Teori:
Når vand fordamper ved en temperatur under kogepunktet vil fordampningshastigheden blandt andet afhænge af temperatur, luftfugtighed og vindhastighed. Når det koger derimod, vil dampens tryk fortrænge den omkringliggende luft, så luftfugtighed og vindhastighed ikke spiller nogen rolle.
Antagelser:
Her vil vi antage, at varmen fra skotørreren får luften til at stige til vejrs, så den fugtige luft derved fjernes som ved kogning. Desuden antages, at varmen fra skotørreren går til at opvarme vandet til 40 °C og derefter fordampe det ved samme temperatur. Varmeudveksling med omgivelserne antages ikke at spille nogen rolle.
Beregning:
Man skal først finde den energi, der forbruges ved tørringen og derefter dividere med skotørrerens effekt for at finde den tid, som den tager.
Opvarmningen bruger energien Qopv = ΔT·cv·m, hvor
ΔT er ændringen i temperatur = (40 - 25) K = 15 K,
cv er vandets specifikke varmekapacitet mellem 25 °C og 40 °C = (4,18 kJ)/(kg·K) og
m er vandets masse = 0,022 kg.
Fordampningen bruger energien Qfor = Lv·m, hvor
Lv er vands fordampningsvarme ved 40 °C = 2406 kJ/kg.
Qopv = (15 K)·(0,022 kg)·(4,18kJ/(kg·K)) = 1,38 kJ
Qfor = (0,022 kg)·(2406 (kJ/kg)) = 52,9 kJ
Dette giver den samlede energi for tørringen: Qtørring = Qopv + Qfor = 1,38 kJ + 52,9 kJ = 54,3 kJ.
Den tid, som det tager skotørreren at producere denne energi, er:
(54,3 kJ)/(4,0 W) = 13575 s = 13575/3600 h = 3,8 h.
Dvs. tørringen tager ca. 4 timer

Svar på opgave 2: Be-10 i atmosfæren
-
Beryllium-10 henfalder ved beta-minus henfald og omdannes til bor-10, en elektron og en antineutrino. Reaktionsskema:
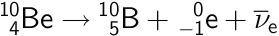
Det bemærkes, at der er bevarelse af både nukleontal (de øverste tal i formlerne) og ladning (de nederste tal). Der er også bevarelse af leptontal, idet elektronen har leptontallet +1 og antineutrinoen har leptontallet -1.
-
Når indholdet af Be-10 i jordens atmosfære er konstant, så betyder det, at der dannes lige så meget Be-10 pr. tidsenhed, som der henfalder. Henfaldet pr. tidsenhed er lig med aktiviteten (A) af Be-10.
Aktiviteten følger formlen: A = k·N = (ln(2)/T½)·(m/M), hvor
T½ er halveringstiden for henfaldet = 1,52·106 år = 1,52·106·(365,25·24·3600) s = 4,80·1013 s
(bemærk: nogle tabeller har værdien T½ = 1,39·106 år),m er massen af Be-10 = 1,2·105 kg og
M er massen af en Be-10 kerne = 10,01 u = 10,01·(1,66·10-27 kg) = 1,662·10-26 kg
Undervejs indgår: k, aktivitetskonstanten, som er lig med ln(2)/T½, og N, antallet af
Be-10 kerner i atmosfæren, der er lig med m/M.Man får med tallene indsat:
A = ln(2)·(4,80·1013 s)-1·(1,2·105 kg)·(1,662·10-26 kg)-1 =
0,693·(4,80)-1·1,2·(1,662)-1·10-13·105·1026 s-1 =
1,043·10-13+5+26 s-1 =
1,043·1017 s-1
Dvs. der dannes 1,0·1017 beryllium-10 kerner pr. sekund i atmosfæren.

Svar på opgave 3: Exoplanet
-
Energimængden (ΔE) er lysintensiteten ved jorden gange linsens tværsnitsareal gange tiden.
Man får: ΔE = (3,0·10-13 W·m-2)·(0,708 m2)·(10·3600 s) = 7,6·10-9 W·s = 7,6·10-9 J
-
For at beregne afstanden, så benytter man, at tyngdekraften er lig med centripetalkraften for planeten. Det forudsættes her, at banen er cirkelformet. Desuden forudsættes det, at planeten er meget lille i forhold til stjernen. Herved kan man regne med, at afstanden mellem stjernen og planeten er lig med radius i den cirkelformede bevægelse.
For tyngdekraften (Ft) mellem stjernen og planeten gælder følgende formel: Ft = G·M·m/r2, hvor
G er gravitationskonstanten = 6,67·10-11 N·m2·kg-2 = 6,67·10-11 m3·kg-1·s-2,
M er stjernens masse = 2,0·1030 kg,
m er planetens masse (går ud),
r er radius i planetens bane = afstanden mellem stjernen og planeten.
For planetens centripetalkraft (Fc) gælder følgende formel: Fc = m·r·(2π/T)2, hvor
T er omløbstiden for planeten i sekunder.
Ved at sætte Ft = Fc får man følgende med hensyn til radius: G·M·m/r2 = m·r·(2π/T)2 ⇒
r = [G·M·T2·(2π)-2]⅓
Man mangler omløbstiden T. Denne bestemmes ud fra nedenstående graf.
Hver spids på grafen svarer til en passage af planeten ind foran stjernen. Hvert mellemrum mellem to spidser svarer til et omløb af planeten omkring stjernen.
Man måler tidsforskellen mellem de to yderste spidser og dividerer med antallet af mellemrum for at finde den gennemsnitlige omløbstid med størst mulige præcision.
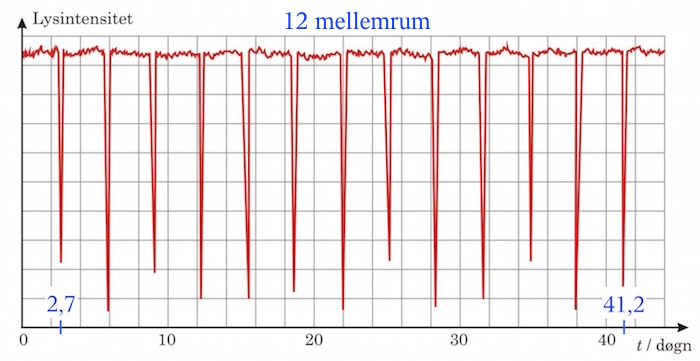
Som vist på grafen sker første passage af planeten efter 2,7 døgn og sidste passage efter 41,2 døgn. Den gennemsnitlige omløbstid er: (41,2 - 2,7)/12 døgn = 3,21 døgn = 3,21·24·3600 s = 2,77·105 s.
Dette indsættes sammen med de andre tal i formlen for radius i cirkelbevægelsen, og man får:
r = [(6,67·10-11 m3·kg-1·s-2)·(2,0·1030 kg)·(2,77·105 s)2·(2π)-2]⅓ = 6,38·109 m
Dvs. afstanden mellem stjernen og exoplaneten er 6,4·109 m

Svar på opgave 4: Træningselastik
-
Elastikken antages at være masseløs og følge Hookes lov: F = -k·x, hvor
F er fjederkraften,
k er fjederkonstanten (k > 0) og
x er udstrækningen af elastikken i forhold til hvile.
For elastikken kan Hookes lov også skrives: F = -k·(l - l0).
l er længden af elastikken og
l0 er længden af den ubelastede elastik.
Hvis man afbilder kraften som funktion af længden af elastikken, og man får en ret linje, så vil k være hældningen. I dette tilfælde regnes der ikke med fortegn, dvs. F = k·(l - l0) = k·l - k·l0.
Man opretter lister med længden af elastikken (længde) og kraften af elastikken (kraft) i Ti-Nspire.
længde:={2.6,2.8,3.,3.2,3.4,3.6,3.8,4.} ▸ {2.6,2.8,3.,3.2,3.4,3.6,3.8,4.} (m)
kraft:={13.8,18.9,23.6,28.5,32.9,38.3,42.7,45.1} ▸ {13.8,18.9,23.6,28.5,32.9,38.3,42.7,45.1} (N)
En afbildning af kraften på elastikken som funktion af dens længde giver følgende graf:
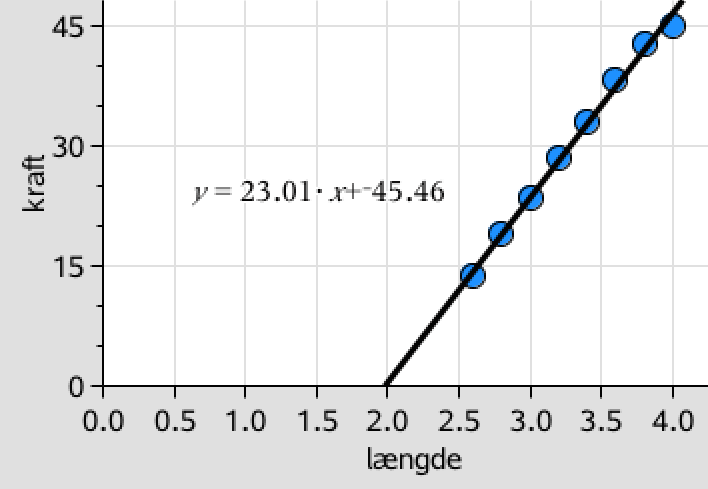
Det ses, at sammenhængen er tilnærmelsesvis retlinet, og at man derfor kan bestemme fjederkonstanten ud fra kurven. Man kan evt. udelade det øverste punkt, da elastikken må formodes at afvige fra Hookes lov, når den nærmer sig bristepunktet.
Hældningen til kurven er, som det fremgår af figuren, 23,0 N·m-1.
Dvs. elastikkens fjederkonstant er 23,0 N·m-1
PS. Længden af den ubelastede elastik kan aflæses til 2,0 m, som er længden, hvor kraften er 0.
-
Effekten findes som ændingen i potentiel energi (ΔE) for elastikken divideret med tiden (Δt). Man har:
ΔE = ½·k·((x2)2 - (x1)2), hvor
x1 er stækningen af elastikken fra start og
x2 er stækningen af elastikken til slut.
Værdien af x1 kan beregnes ved hjælp af Hookes lov: 20 N = (66 N·m-1)·x1 ⇒ x1 = (20 N)/(66 N·m-1) = 0,303 m.
Man har at x2 = x1 + 0,19 m = 0,303 m + 0,19 m = 0,493 m.
P = ΔE/Δt = ½·(66 N·m-1)·((0,493 m)2 - (0,303 m)2)/(1,5 s) = 3,33 Nm/s = 3,33 W.
Dvs. hånden udfører i gennemsnit effekten 3,3 W under øvelsen.
PS. I den vedlagte vejledning er der vist en alternativ metode.

Svar på opgave 5: Kraftsensor
-
Det antages, at trykket (p) er jævnt fordelt på sensoren. Der gælder: p = F/A, hvor
F er kraften som sensoren påvirkes med = 10,0 N og
A er sensorens overfladeareal = 2,62·10-4 m2.
Man får, at det maksimale tryk på sensoren er (10,0 N)/(2,62·10-4 m2) = 3,82 N·m-2
-
Det antages, at Ohms lov gælder. Spændingsfaldet over RFSR mindskes med resistansen eller rettere RFSR's andel af kredsens samlede resistans. Dette er dog det samme, når R holdes konstant.
Det fremgår af nedenstående diagram, at RFSR er 11 kΩ, når kraften er 0,4 N, og at den aftager med voksende kraft.
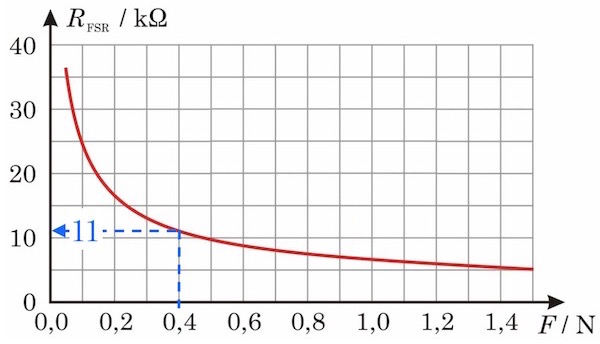
Man skal derfor finde R, når kraften er 0,4 N og Uud derved er 2,7 V.
Man finder kredsens strømstyrke: I = (2,7 V)/(11 kΩ) = 0,000245 A. Denne er ens for begge modstande, da de er serieforbundne.
Dette giver: R = (5,0 - 2,7 V)/(0,000245 A) = 9,4 kΩ

Svar på opgave 6: Badminton
-
For tyngdekraften (Ft) gælder: Ft = m·g, hvor
m er massen af fjerbolden = 5,0·10-3 kg og
g er tyngdeaccelerationen = 9,82 m·s-2
Dvs. tyngdekraften er (5,0·10-3 kg)·(9,82 m·s-2) = 4,9·10-2 N
-
Den vandrette distance, som fjerbolden tilbagelægger er lig med arealet under den røde kurve. Dette areal er målt nedenunder i Geogebra ved hjælp af polygonværktøjet.
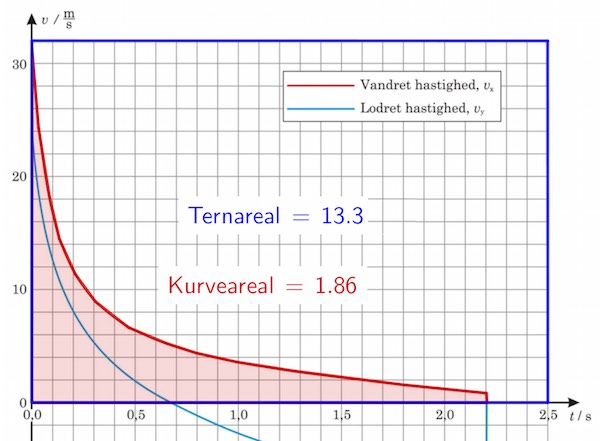
Den blå ramme indeholder 16·25 tern = 400 tern. Denne ramme har et areal i Geogebra på 13,3. Samtidig svarer det til en distance på (2,5 s)·(32 m/s) = 80 m. Arealet under kurven er i Geogebra 1,86, hvilket svarer til en længde på (80 m)·(1,86/13,3) = 11,2 m.
Dvs. fjerbolden bevæger sig 11 m vandret.
-
Ved banens toppunkt er den lodrette hastighed 0, dvs. den blå kurve skærer x-aksen i dette punkt. Man aflæser den tilsvarende værdi for den vandrette hastighed i toppunktet til 5,1 m/s som vist nedenunder:
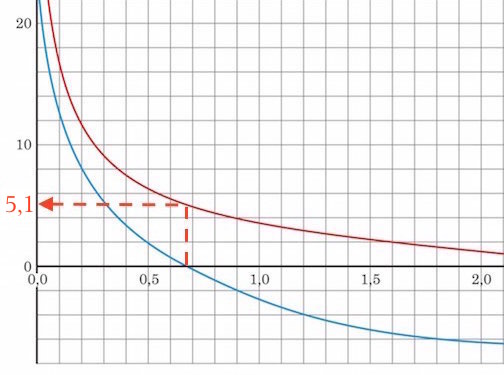
Formfaktor:
Man vælger, at se på fjerbolden i toppunktet. Her gælder, at |Fl| er lig med den numeriske værdi af fjerboldens vandrette (negative) acceleration, av, gange dens masse. Accelerationen kan beregnes af kurverne som hældningen til den røde kurve i toppunktet.
Formlen for luftmodstandskraften er |Fl| = ½·ρ·c·A·v2, hvor
ρ er luftens densitet = 1,293 kg/m3,
c er formfaktoren (dimensionsløs),
A er fjerboldens tværsnitsareal i bevægelsesretningen = 28 cm2 = 28·(10-2 m)2 = 2,8·10-3 m2 og
v er fjerboldens vandrette fart = 5,1 m/s.
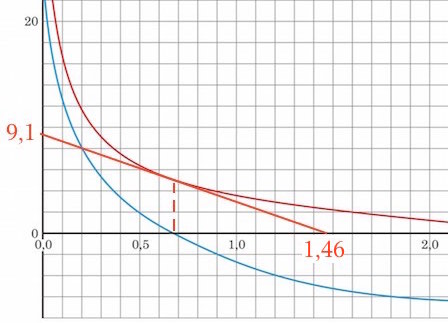
Man har: |av| = |(0-9,1 m/s)/(1,46-0 s)| = 6,23 m·s-2.
Man får følgende formfaktor: |av|·m = ½·ρ·c·A·v2 ⇒ c = 2·|av|·m·ρ-1·A-1·v-2 ⇒
c = 2·(6,23 m·s-2)·(5,0·10-3 kg)·(1,293 kg/m3)-1·(2,8·10-3 m2)-1·(5,1 m/s)-2 = 0,66
Generel beregning af formfaktor
Som eksempel vælges punktet for t=1,0 s på banekurven. Der gælder følgende kraftdiagram, hvor fjerbolden er vist med en cirkel:
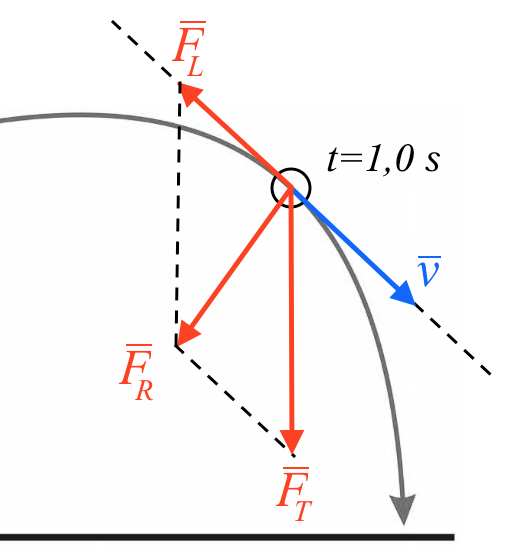
Forklaring:
v er hastighedsvektoren, som ligger på tangenten til kurven. Der gælder: v = (vx,vy), hvor vx og vy er hastigheden for fjerbolden i henholdsvis x- og y-aksens retning.
FL er luftmodstandskraften som vektor. Denne er modsatrettet hastighedsvektoren (gælder for alle gnidningskræfter).
FT er tyngdekraften som vektor. Denne er lodret nedadrettet.
FR er den resulterende kraft = FL + FT.
Bemærk at ovenstående tegning rummer tre koordinatsystemer i eet: et xy-koordinatsystem for boldens placering, et vxy-koordinatsystem for dens hastighed og et axy-koordinatsystem for dens acceleration og dermed for kræfterne på den.
Man får følgende for |FL|: FR = FL + FT ⇒ FL = FR - FT ⇒ |FL| = |FR - FT|.
FR = m·(ax,ay), hvor m er massen af fjerbolden, mens ax og ay er fjerboldens acceleration i henholdsvis x- og y-aksens retning (Newtons anden lov).
På figuren nedenunder er ax og ay beregnet (røde tangenter), mens vx og vy er aflæst (blå pile). Begge dele er gjort for t = 1,0 s.
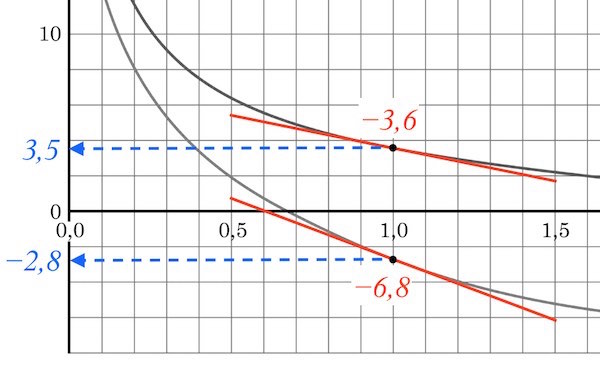
For hastigheden får man: v = (3,5 m/s;-2,8 m/s). Dette giver farten: |v| = |(3,5 m/s;-2,8 m/s)| = √[3,52 + (-2,8)2] m/s = 4,48 m/s.
For den resulterende kraft får man: FR = m·(ax,ay) = (5,0·10-3 kg)·(-3,6 m/s2;-6,8 m/s2) = (−0,018 N;−0,034 N).
Der gælder: FT = (5,0·10-3 kg)·(0;-9,82 m/s2) = (0;-0,0491 N). Tyngdekraftens andenkoordinat er negativ, fordi tyngdekraften peger nedad, mens positiv retning er opad.
Man finder nu: FL = FR - FT = (-0,018 N;-0,034 N) − (0;-0,0491 N) = (-0,018 N; 0,015 N)
Dvs. |FL| = |(-0,018 N; 0,015 N)| = √[0,0182 + 0,0152] N = 0,0234 N.
Dette indsættes i formlen for formfaktoren: |FL| = ½·ρ·A·c·|v|2 ⇒
c = 2·|FL|·ρ-1·A-1·|v|-2 = 2·(0,0234 N)·(1,293 kg/m3)-1·(2,8·10-3 m2)-1·(4,48 m/s)-2 = 0,64
Specialtilfælde: toppunkt og nedslagspunkt
I toppunktet gælder som nævnt, at FL er lig med FR's vandrette komposant Dette er vist nedenunder.
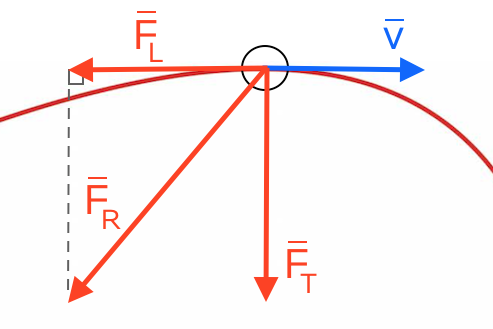
Det er denne, som man beregner længden af ved hjælp af hældningen til kurven for fjerboldens vandrette fart i toppunktet og fjerboldens masse.
Lige inden nedslagspunktet nærmer fjerbolden sig et lodret fald med konstant fart. Hvis denne tilstand var nået, så vil den resulterende kraft være 0 (Newtons første lov), og man kunne sætte |FL| lig med |FT|. Det skete dog ikke i dette tilfælde.

Svar på opgave 7: JET energirekord
-
I en kubikmeter af plasma er der 7,3·1019 elektroner. Antallet af elektroner er lig med summen af deuteriumker og tritiumkerner. Da der er lige mange af de to kerner, så gælder:
antal deuteriumkerner pr. m3 = antal tritiumkerner pr. m3 = ½·7,3·1019 m-3 = 3,65·1019 m-3.
Massen af en deuteriumkerne er 2,014 u = 2,014·1,66·10-27 kg = 3,34·10-27 kg
Massen af en tritiumkerne er 3,016 u = 3,016·1,66·10-27 kg = 5,01·10-27 kg
Der ses bort fra massen af elektroner. Masse af plasmaet bliver: massen af deuterium pr. m3 + massen af tritium pr. m3 gange rumfanget af tokamakken =
3,65·1019 m-3·(3,34·10-27 kg + 5,01·10-27 kg)·(82,3 m3) = 2,5·10-2 g
-
For fusion mellem to slags kerner, der optræder med lige stor tæthed, gælder: P = Q·¼·n2·σ·v12·V, hvor
P er gennemsnitseffekten ved fusionen for alle kerner, der reagerer,
Q er tabelværdien for energiproduktionen i fusionen mellem en deuteriumkerne og en tritiumkerne
= 17,6 MeV = 17,6·1,602·10-13 J = 2,82·10-12 J,n er tætheden af kerner = 7,3·1019 m-3,
σ·v12 reaktiviteten og
V er volumen af reaktor = 82,3 m3.
Gennemsnitseffekten for processen kan aflæses af grafen, idet man ser bort fra opvarmning og afkøling:
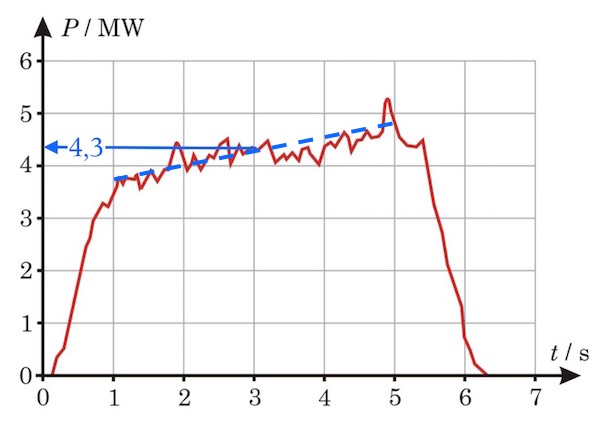
Man antager som vist, at effekten stiger jævnt gennem processen og aflæser gennemsnitseffekten til 4,3 MW = 4,3·106 J/s.
Man får: P = Q·¼·n2·σ·v12·V ⇒
σ·v12 = 4·Q-1·n-2·V-1·P ⇒
σ·v12 = 4·(2,82·10-12 J)-1·(7,3·1019 m-3)-2·(82,3 m3)-1·(4,3·106 J/s) =
1,4·10-23 m3·s-1