Svar på opgave 1: Proptrækker

1. Densiteten er masse divideret med volumen af vin:

   (0,73 kg)/(0,75 L) = 0,973333 kg/L = 0,97 kg/L

2. Den gennemsnitlige effekt er det samlede arbejde divideret med tiden. Arbejdet findes som arealet under kurven.

   Man måler figurens areal i Geogebra ved hjælp af polygonværktøjet. Samtidig måler man arealet af hele det ternede område med samme værktøj. Dette er vist nedenunder:

   

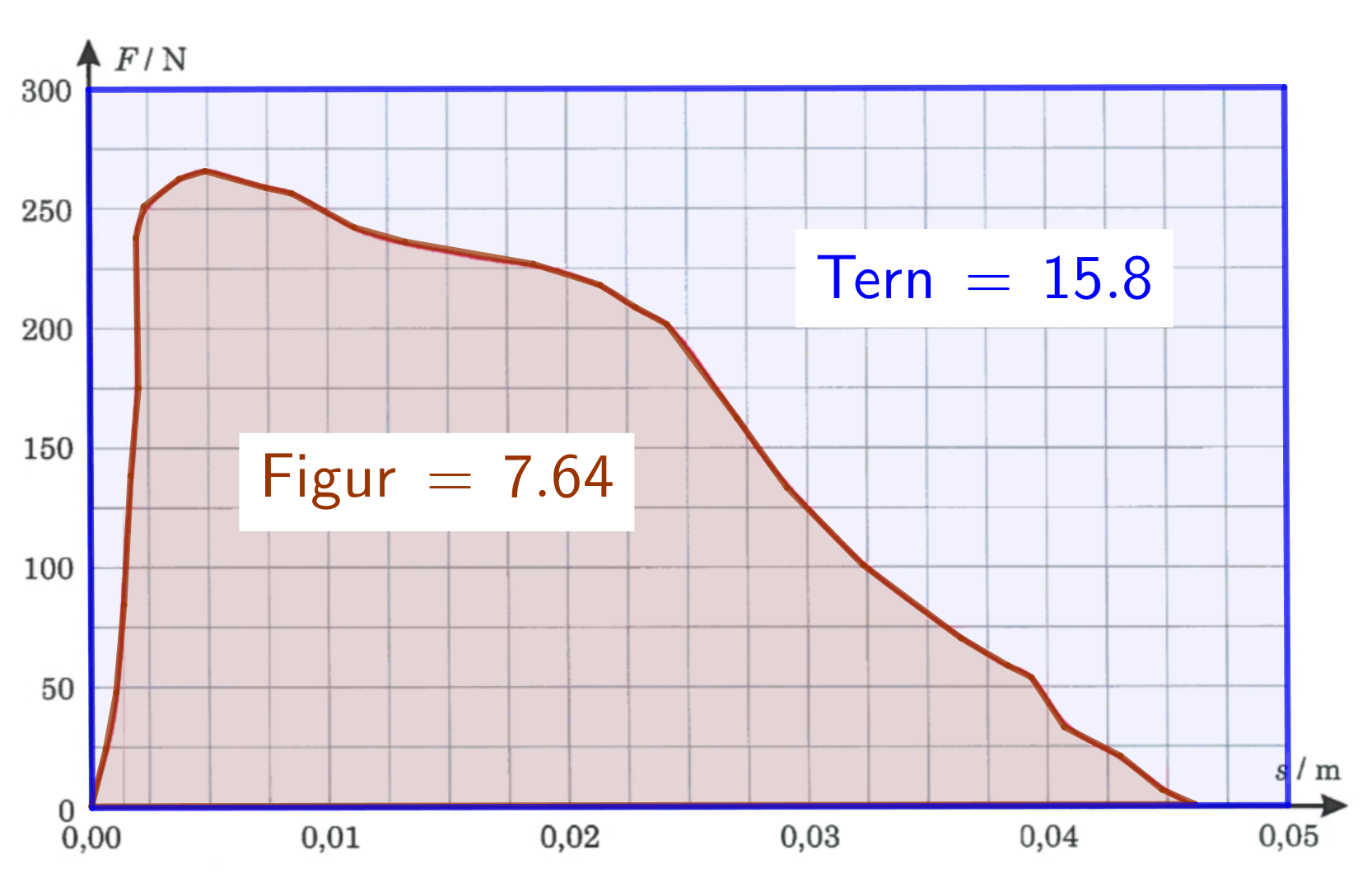
   Det ternede område har et areal i Geogebra på 15,8. Dette areal svarer til 300·0,05 N·m = 15 J.

   Det samlede arbejde er 15 J gange figurens areal divideret med det ternede områdes areal = (15 J)·7,64/15,8 = 7,25 J.

   Dvs. effekten er (7,25 J)/(2,3 s) = 3,2 W

Svar på opgave 2: PET scanning med ¹³N

1. Det antages, at een proton støder ind i een O-16 isotop. Man kalder den ukendte kerne (nuklid) for A, antallet af dens nukleoner (massenummeret) kaldes x, og antallet af dets protoner (atomnummeret) kaldes y. Dette er vist nedenunder:

   

   Summen af massenumre skal stemme før og efter reaktionen. Det sammen gælder atomnumre.

   Det ses, at 16 + 1 = 13 + A ⇒ A = 4 og 8 + 1 = 7 + Z ⇒ Z = 2. Man får derfor, at X er He-4.

   Man får den endelige kerne-reaktion:

   

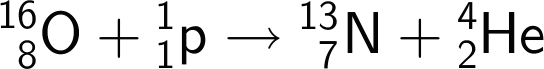
2. Halveringstiden for henfald af N-13 er 9,96 min. Formlen for aktiviteten som funktion af tiden (A(t)) af N-13 er

   A(t) = A₀·(0,5)^t/T, hvor

      A₀ er startaktiviteten i Bq (eller s^-1),

      t er tiden i sekunder og

      T er halveringstiden (= 9,96 min. i følge tabel).

   Man finder aktiviteten fra start ved at løse følgende ligning med hensyn til A₀:

   575 MBq = A₀·(0,5)^{(15 min)/(9,96 min)}

   Dette gøres i Ti-NSpire:

   solve(575*mbq=a_0*(0.5)^{(15*minut)/(9.96*minut)},a_0)|mbq=10⁶*bq ▸ a_0=1.63315·10⁹Bq

   Dvs. aktiviteten af N-13 lige efter fremstillingen var 1,63315·10⁹ Bq = 1,63 GBq

3. Aktiviteten er antal henfald pr. tidsenhed. Det samlede antal henfald over en periode er integralet af A(t) = A₀·(0,5)^{t/(9,96 min)} fra t = 15 min til t = 45 min.

   Man får følgende i Ti-Nspire:

   integral(1.63*10⁹*bq*(0.5)^{t/(9.96*minut)},t,15,45*minut)|bq=60/minut ▸ 4.34287·10¹¹

   Dvs. antallet af henfald er 4,34287·10¹¹. Hvert henfald giver en energi på 189 fJ. Det giver en samlet afsat energi på:

   4,34287·10¹¹·189 fJ = 4,34287·10¹¹·189·10^-15 J = 0,0821 J

   (Man kan også integrere fra det tidspunkt, hvor N-13 indsprøjtes: integral(575*10⁶*bq*(0.5)^{t/(9.96*minut)},t,0,30*minut)|bq=60/min ▸ 4.34287·10¹¹)

Svar på opgave 3: Skærmfilter

1. Gitterlinjernes afstand følger formlen:

   d = (n·λ)/sin(φ_n), hvor

      n er ordenen af linjen,

      λ er lysets bølgelængde i m,

      d er gitterlinjeafstanden i m og

      φ_n er vinklen for den n-te ordens lysstråle.

   Man vælger for nøjagtighedens skyld, at bruge det yderste punkt på figuren, der svarer til afbøjningen med sjette orden eller afbøjningen med n = 6.

   Der gælder, at sin(φ₆) er afstanden mellem nul-te og sjette-ordens punkterne divideret med afstanden fra filteret til væggen, dvs. sin(φ₆) = ((16 - 10) cm)/(120 cm) = 0,05. Man får:

   d = (6·532·10^-9 meter)/0,05 = 63,84·10^-6 m

   Afstanden mellem gitterlinjerne er 64 μm

Svar på opgave 4: NTC resistor

1. Man finder effekten (P) med formlen

      P = I²·R, hvor

      I er strømstyrken i A og

      R er resistansen i Ω

   P = I²·R = (1,9·10^-3 A)²·25·10³ Ω = 1,9²·25·10^-6·10³ Ω·A² = 0,09025 W

   Dvs. effekten er 0,090 W

2. Man skal finde R_NTC ud fra R og de to kendte spændingsfald, dvs. man skal finde en forskrift for R_NTC, hvor strømstyrken I ikke indgår.

   Man benytter, at I dels er lig med den samlede spænding divideret med den samlede modstand, dels er lig med spændingen over NTC-modstanden divideret med NTC-modstandens resistans. Dette giver:

   I = U/(R + R_NTC) ∧ I = U_NTC/R_NTC ⇒ U/(R + R_NTC) = U_NTC/R_NTC ⇒ R_NTC = R/(U/U_NTC - 1)

   Man får: R_NTC = (31 kΩ)/((12 V)/(3,5 V) - 1) = 12,7647 kΩ ≈ 13 kΩ.

   

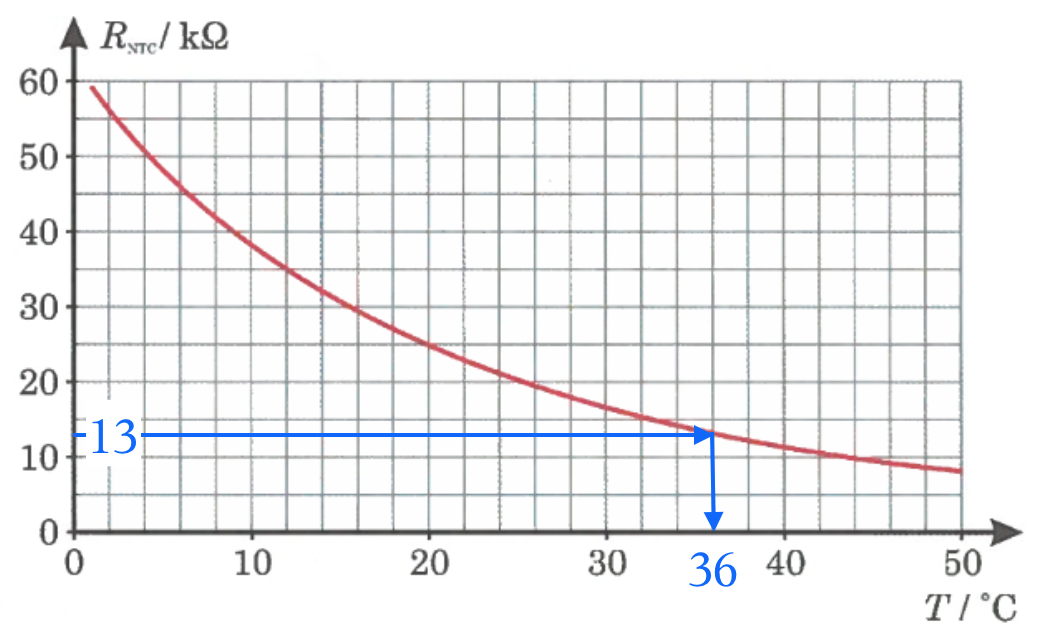
   NTC-resistorens temperatur aflæses til 36 °C

Svar på opgave 5: E-cigaret

1. Tiden (t), der går før batteriet skal genoplades, følger formlen:

   t = Q·U/P, hvor

      Q er ladningen i C,

      U er spændingsfaldet i V og

      P er effekten i W.

   t = (5,04·10³ C·3,7 V)/(5,5 W) = 3390,55 s.

   Dette omregnes til minutter: (3390,55/60) min = 56,5092 min.

   Dvs. der går 57 min før batteriet skal genoplades.

2. Man skal opvarme 1,2-propandiol fra 20 °C til 187 °C og få det til at fordampe. Formlen er

   P = m·ΔT·c + m·L, hvor

      m er massen af 1,2-propandiol, der opvarmes og fordampes pr. sekund,

      ΔT er det antal grader Kelvin som 1,2-propandiolen bliver opvarmet inden fordampning,

      c er 1,2-propandiols specifikke varmekapacitet i J/(g·K) og

      L er 1,2-propandiols specifikke smeltevarme i J/g.

   Man løser ligningen med hensyn til m i Ti-Nspire:

   solve(5.5*watt=m*(187-20)*kelvin*2.51*joule/(gr*kelvin)+m*711*joule/gr,m)|joule=watt*sek ▸ m=0.004867*gr/sek

   Dvs. massen af 1,2-propandiol, der fordampes pr. sekund, er 4,87 mg

Svar på opgave 6: Alcator C-Mod

1. Den maksimale størrelse af magnetfeltet (B) følger formlen:

   B = μ₀·N·I/(2·pi·r), hvor

      μ₀ er vakuumpermeabiliteten i N·A²

      N er antallet vindinger

      I er den maksimale strømstyrke i A

      r er storradius i meter. (Torussen er en vandretliggende ring. Ses den overfra er storradius
      gennemsnittet af ydre og indre radius af ringen.)

   B = (1,257·10^-6·(T·m/A)·120·250·10³ A)/(2·π·0,67 m) = 8,95781 T

   Dvs. den maksimale størrelse af magnetfeltet i torussen er 8,96 T

2. Formlen for tætheden af deuterium i plasmaet er:

   dn/dt = n₁·n₂·σ·v₁₂, hvor

      dn/dt er reaktionsraten,

      n₁ antallet af D atomer,

      n₂ antallet af He atomer og

      σ·v₁₂ er aktiviteten for reaktionen af de to atomer.

   Aktivitet aflæses på den dobbeltlogaritmiske graf til 6,5·10^-27 m³·s^-1.

   Reaktionsraten, dn/dt, ved 58 MK er oplyst til 6,4·10¹² m^-3·s^-1.

   Det bemærkes, at n₁ = n₂, dvs. formlen bliver til dn/dt = n₁²·σ·v₁₂. Dette løses med hensyn til n₁:

   n₁ = √[(6,4·10¹² m^-3·s^-1)/(6,5·10^-27 m³·s^-1)] = 3,13786·10¹⁹·m^-3

   Dvs. tætheden af deuterium i plasmaet er 3,14·10¹⁹ m^-3

Svar på opgave 7: Curiosity

1. Den tid (ΔT), som sidste fase af landingen tager følger formlen:

   ΔT = s/v, hvor

      s er afstanden i m og

      v er farten af rumsomden i m·s^-1.

   Dvs. sidste fase tager (20 m)/(0,6 m·s^-1) = 33,3333 s = 33,3 s

2. Ændringen i mekanisk energi er ændringen i potetiel energi plus ændringen i kinetisk energi.

   3,3·10³ kg·(3,72 m·s^-2)·(125 - 1,5)·10³ m + 0,5·((5,9·10³ m·s^-1)² - (79 m·s^-1)²)) = 5,89423·10¹⁰ J.

   Dvs. ændring i mekanisk arbejde for rumsonden er 59 GJ

   (Man kan også bruge formlen potentiel energi ved massetiltrækning: E = G·(m₁·m₂)/r. Så får man 60 GJ).

3. Der sker en opbremsning, derfor må luftens kraft være større end tyngdekraften.

   Luftens kraft er 0,5·c·ρ·A·v², hvor

      c er faldskærmens formfaktor

      ρ er luftens densitet i kg/m³

      A er faldskærmens areal på tværs af bevægelsesretningen i m²

      v er faldskærmens fart i m/s

   A beregnes som: pi gange radius i anden = π·((21,35 m)/2)² = 358,0 m²

   Tyngdekraftens størrelse er m·g, hvor

      m er massen i kg og

      g er tyngdeaccelerationen på Mars.

   Resulterende kraft:

   3,3·10³ kg·3,72 m·s^-2 - 0,5·0,02 kg·m^-3·0,66·358,0 m²·(79 m·s^-1)² = -2470,32 N

   Den resulterende kraft er -2470,32 N, dvs. luftens kraf er større end tyngdekraften, hvilket vil sige, at der sker en opbremsning.

   Accelerationen er den resulterende kraft divideret med massen af rumsonden: Acc = (-2470,32 N)/(3,3·10³ kg) = 0,748582 m·s² = 0,749 m·s²