Svar på opgave 1: Solfanger

1. I følge Ohms lov gælder: I = U/R, hvor

      I er strømstyrken, U er spændingen og R er resistansen.

   Dette giver I = 12V/(9,3 Ω) = 1,29 A

   Dvs. strømstyrken gennem ventilatoren er 1,3 A

2. Nyttevirkningen (η) er: P_U/P_T, hvor

      P_U er udnyttet effekt og

      P_T er tilført effekt = 588 W.

   Den udnyttede effekt bruges til at opvarme luften. Den beregnes ved formlen:

   P_U = m_L·c_p,L·ΔT/Δt, hvor

      m_L er massen af luft, der passerer i timen = 95 kg = 9,5·10⁴ g,

      c_p,L er den specifikke varmekapacitet af luft = 1,00 J·g^-1·K^-1,

      ΔT er temperaturændringen for luften = (17 - 8,0) K = 9,0 K og

      Δt er tiden = 1 time = 3600 s.

   Dette giver: (9,5·10⁴ g)·(1,00 J·g^-1·K^-1)·(9 K)/(3600 s) = 237,5 J/s = 238 W

   Dvs. nyttevirkningen er: (238 W)/(588 W) = 0,4048 = 40 %

Svar på opgave 2: Dykning i Det Røde Hav

1. Der gælder følgende lineære sammenhæng mellem vandtryk (p) og dybden (h):

   p = h·ρ·g + p₀, hvor

      p₀ er luftens tryk ved vandoverfladen,

      ρ er vandets densitet og

      g er tyngdeaccelerationen = 9,82 m·s^-2

   Man laver et plot af tallene for p mod tallene for h:

   

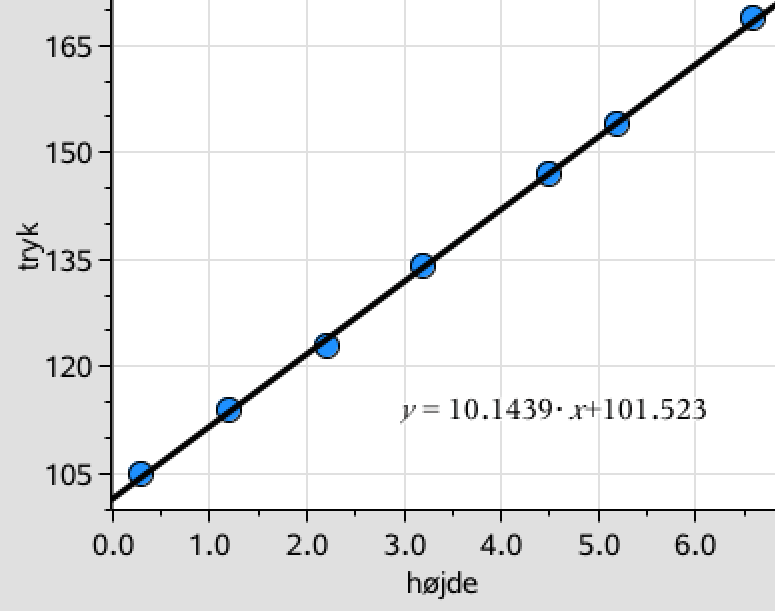
   Som det ses, er tendenslinjen en ret linje med ligningen y = 10,1439·x + 101,523.

   Dvs. med 3 betydende cifre gælder sammenhængen: p = (10,1 kPa/m)·h + 102 kPa

2. Man har fra foregående spørgsmål:

      p = h·ρ·g + p₀ og p = (10,1 kPa/m)·h + 102 Pa. Dette vil sige, at: ρ·g = 10,1 kPa/m.

   Idet kPa/m = 10³ N·m^-3 = 10³ kg·m^-2·s^-2, så får man:

      ρ·g = 10,1·10³ kg·m^-2·s^-2 ⇒

      ρ = (10,1·10³ kg·m^-2·s^-2)/(9,82 m·s^-2) = 1,029·10³ kg·m^-3.

   Dvs. vandets densitet er 1,03·10³ kg·m^-3

Svar på opgave 3: Nattehimlens klareste stjerne

1. Man bruger Stefan-Boltzmanns lov for at finde den effektive overfladetemperatur af stjernen.

   L = 4·π·R²·σ·T⁴, hvor

      L er stjernen luminositet (samlede effekt i W) = 8,96·10²⁷ W,

      R er stjernens radius = 1,22·10⁹ m,

      σ er Stefan-Boltzmanns konstant = 5,6704·10^-8 W·m^-2·K^-4 og

      T er den effektive temperatur af stjernens overflade i K.

   Heraf fås: T = ⁴√[(8,96·10²⁷ W)·(4·π)^-1·(1,22·10⁹ m)^-2·(5,6704·10^-8 W·m^-2·K^-4)^-1] = 9587 K.

   Dvs. Sirius A's overfladetemperatur er 9,59·10³ K

Svar på opgave 4: Skydiving

1. Accelerationen findes som hældningen til kurven punktet for t = 5 sek. Denne hældning er vist på figuren nedenunder:

   

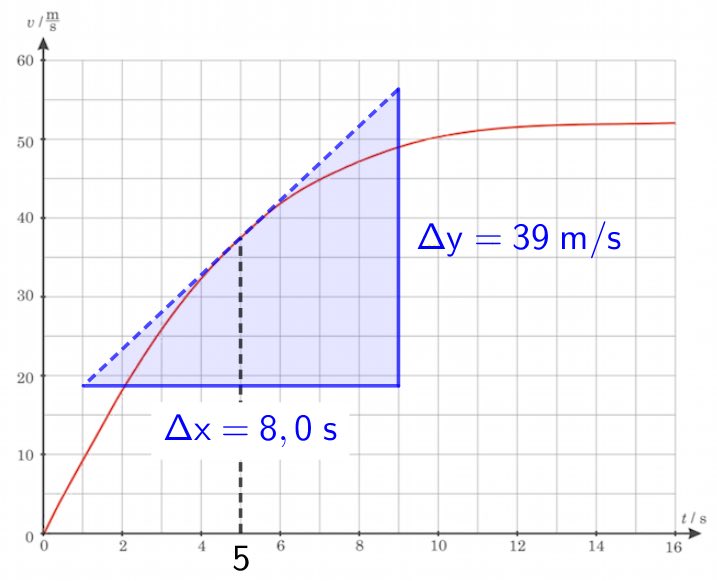
   Accelerationen bliver: Δy/Δx = (39 m/s)/(8,0 s) = 4,875 m·s^-2

   Dvs. faldskærmsudspringerens acceleration efter 5 sekunder er 4,9 m·s^-2

2. Den tilbagelagte strækning er integralet under kurven, som tænkes fortsat med en vandret linje efter t = 16 s, idet faldskærmsudspringeren på dette tidspunkt har nået sin sluthastighed.

   På nedenstående figur er arealet under kurven fra t = 0 til t = 16 s beregnet i Geogebra. Arealet af hele den ternede del af grafen er også beregnet for at kunne omregne fra Geogebras enheder til grafens enheder.

   

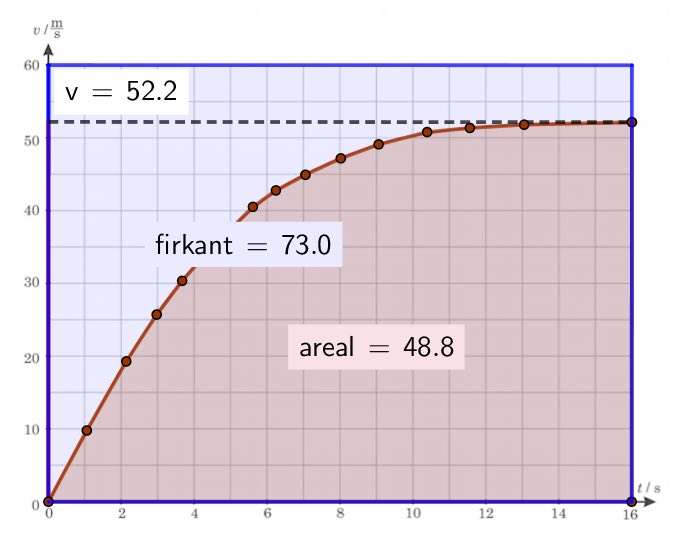
   Arealet af hele det ternede område svarer til en distance på (16 s)·(60 m/s) = 960 m i virkeligheden. I Geogebras koordinatsystem svarer denne distance til 73,0 enheder. Dvs. 1 enhed i Geogebra svarer til (960 m)/73,0 = 13,2 m.

   Arealet under kurven er ved hjælp af Geogebras polygon-værktøj fundet til 48,8 Geogebra-enheder, som svarer til 48,8·(13,2 m) = 644 m. Dette er den tilbagelagte distance efter 16 sekunder.

   Som det ses ovenfor findes sluthastigheden på kurven til 52,2 m/s. Her er Geogebra-længden fra 0 til den stiplede linje målt og divideret med Geogebra-længden fra 0 til 60-linjen. Dette forhold er så ganget med 60 m/s.

   Faldskærmsudspringeren mangler at falde (2000 - 644) m = 1356 m. Dette sker med en konstant fart af 52,2 m/s. Der gælder: tid er lig med distance divideret med (gennemsnits-) fart, dvs. den resterende tid for faldet er: (1356 m)/(52,2 m/s) = 26,0 s.

   De 16 og 26 sekunder lægges sammen, og man får, at det tager 42 sekunder for faldskærms­udspringeren at falde 2000 m.

Svar på opgave 5: Mikrobatteri

1. Ni-63 henfalder ved beta-henfald og bliver til Cu-63 plus en elektron og en antineutrino. Reaktionsskemaet er:

   

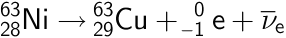
2. Man opretter lister med spænding (spænding) og strømstyrke (strøm) i Ti-Nspire:

   spænding:={110,100,95,90,85,80,70,60,50,25} ▸ {110,100,95,90,85,80,70,60,50,25}

   strøm:={0.51,0.89,1.15,1.32,1.48,1.61,1.75,1.87,2.,2.25} ▸ {0.51,0.89,1.15,1.32,1.48,1.61,1.75,1.87,2.,2.25}

   Man laver en liste med effekter. Effekt er størmstyrke gange spænding.

   effekt:=strøm*spænding ▸ {56.1,89.,109.25,118.8,125.8,128.8,122.5,112.2,100.,56.25}

   Man ser på en afbildning af effekten som funktion af spænding. Denne ses, at kunne tilnærmes til et tredjegradspolynomium som vist nedenunder.

   

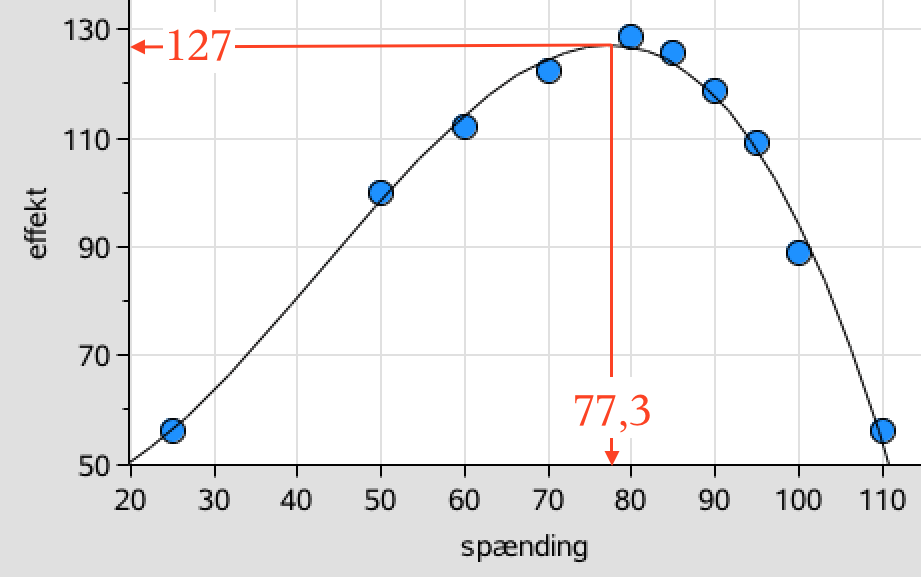
   Ovenover er den maksimale effekt og den spænding, der giver den største effekt vist. Disse værdier er fundet ved tredjegradspolynomie-regression i Ti-Nspire:

   CubicReg spænding,effekt,1: CopyVar stat.RegEqn,f2: stat.results ▸
   [["Titel","Tredjegradsregression"]
   ["RegEqn","a*x^3+b*x^2+c*x+d"]
   ["a",−0.000498]
   ["b",0.063636]
   ["c",−0.905145]
   ["d",46.9625]
   ["R²",0.991532]
   ["Resid","{...}"]]

   Regressionsfunktionen er: f2(x) = −0,000498·x³ + 0,06364·x² - 0,9051·x + 46,96.

   Den spænding, der giver den største effekt, findes ved hjælp kommandoen fMax i Ti-Nspire:

   fMax(f2(x),x)|25<x<110 ▸ x=77.316

   Den maksimale effekt er: f2(77,316) = 127,11.

   Dvs. den maksimale effekt er 127 mV·nA = 127·10^-3-9 W = 1,27·10^-10 W og

   den spænding, der giver den største effekt er 77,3·10^-3 V = 7,73·10^-2 V

3. Man skal finde massen af Ni-63 kerner, hvorom der gælder:

   m = N·m_k, hvor

      m er massen af alle Ni-63 kerner

      N er antallet af Ni-63 kerner og

      m_k er massen af en Ni-63 kerne = 62,93 u = 62,93·(1,661·10^-24 g) = 1,045·10^-22 g.

   For N har man henfaldsloven:

   A = k·N ⇒ N = A/k, hvor

      A er aktiviteten = antal dannede elektroner pr. sekund ved beta-henfald og

      k er henfaldskonstanten.

   For henfaldskonstanten, k, gælder:

   k = ln(2)/T_1/2, hvor

      T_1/2 er halveringstiden for henfald af Ni-63 = 100 år = 100·365,25·24·3600 s = 3,156·10⁹ s.

   Man har følgende sammenhæng mellem A og strømstyrken i mikrobatteriet:

   I = η·A·e ⇒ A = I/(η·e), hvor

      I er strømstyrken = 2,40 nA = 2,40·10^-9 C/s og

      η er mikrobatteriets nyttevirkning = 15 % = 0,15,

      e er elementarladningen for en elektron = 1,602·10^-19 C.

   Det kan samles til følgende beregning for massen af Ni-63:

   m = N·m_k = (A/k)·m_k = ((I/(η·e))/k)·m_k = ((I/(η·e))/(ln(2)/T_1/2))·m_k = I·T_1/2·m_k/(η·ln(2)·e) =

      (2,40·10^-9 C/s)·(3,156·10⁹ s)·(1,045·10^-22 g)/(0,15·0,6931·(1,602·10^-19 C)) = 0,04752 g

   Dvs. massen af Ni-63 som skal bruges i mikrobatteriet er 0,04752 g = 47,5 mg

Svar på opgave 6: Eridani B

1. Ved hjælp af Wiens forskydningslov får man:.

   λ_max = (2,898·10^-3 m·K)/T, hvor

      λ_max er den bølgelængde, der giver den maksimale intensitet og

      T er stjernens effektive overfladetemperatur = 1,68·10⁴ K.

   Dvs. den bølgelængde, der giver den største intensitet, er (2,898·10^-3 m·K)/(1,68·10⁴ K) = 1,725·10^-7 m = 173 nm

2. Man skal finde effekten (I) af stjernens lys ved jordoverfladen, idet det antages at stjernen er kugleformet, at den lyser ens i alle retninger og idet, der ses bort fra lystab i atmosfæren. Man bruger afstandskvadratloven:

   I = L/(4·π·R²), hvor

      I er effekten pr. m² af stjernens lys ved jordoverfladen,

      R er afstanden fra stjernen til jorden = 16,5 lysår = 16,5·(9,461·10¹⁵ m) = 1,561·10¹⁷ m og

      L er stjernens samlede effekt ved dens overflade.

   L kan findes ved hjælp af Stefan-Boltzmanns lov (som i opgave 3):

   L = 4·π·r²·σ·T⁴, hvor

      r er stjernens radius = 9,47·10⁶ m,

      σ er Stefan-Boltzmanns konstanten = 5,670·10^-8 W·m^-2·K^-4 og

      T er stjernens effektive overfladetemperatur = 1,68·10⁴ K (som i spørgsmål 6a).

   Man får: I = L/(4·π·R²) = 4·π·r²·σ·T⁴/(4·π·R²) = (r/R)²·σ·T⁴

   Samtidig gælder, at: I = (E/Δt)/a, hvor

      E er energien af det lys, der rammer kikkerten = 5,0·10^-8 J,

      Δt er tiden, hvor kikkerten modtager lys fra stjernen og

      a er kikkertens linse-areal = 0,20 m².

   Dette samles: I = (r/R)²·σ·T⁴ = (E/Δt)/a, der giver følgende ligning med hensyn til Δt:

   Δt = (E/a)/((r/R)²·σ·T⁴) =

   ((5,0·10^-8 J)/(0,20 m²))/(((9,47·10⁶ m)/(1,561·10¹⁷ m))²·(5,670·10^-8 W·m^-2·K^-4)·(1,68·10⁴ K)⁴) =

   15039 s = 15039·(1 time/3600) = 4,178 timer.

   Dvs. kikkerten belyses i 4,2 timer

Svar på opgave 7: Båd for anker

1. Effekten er den numeriske værdi af skalarproduktet mellem kraftvektoren og hastighedsvektoren.

   I dette tilfælde, hvor kraftvektor og hastighedsvektor er parallelle, får man, at effekten er kraft gange fart, som er (386 N)·(18 m/min) = (386 N)·(18 m/(60 s)) = 115,8 Nm·s^-1.

   Dvs. elmotorens effekt er 116 W

2. Vandet antages at være havvand med 2% saltholdighed, der svarer til gennemsnittet for danske farvande. Opdriften på ankeret (F_o) er tyngden af det saltvand, som ankeret fortrænger (F_v).

   Dette kan skrives: F_o = F_v = m_v·g = (V_v·ρ_v)·g = (V_an·ρ_v)·g ⇒ F_o = ((m_an/ρ_al)·ρ_v)·g. Her er:...

      m_v massen af fortrængt saltvand,

      V_v er rumfanget af fortrængt saltvand,

      m_an er massen af ankeret = 14,4 kg,

      ρ_v er massefylden af saltvand = 1,014 kg·m^-3,

      ρ_al er massefylden af aluminium (= massefylden af ankeret) = 2,699 kg·m^-3 og

      g er tyngdeaccelerationen = 9,82 m·s^-2.

   Dvs. den færdige formel er, at opdriften er er massen af ankeret gange forholdet mellem massefylderne af vand og aluminium ganget med tyngdeaccelerationen.

   Dette giver F_o = (14,4 kg/(2,699 kg·m^-3))·(1,014 kg·m^-3)·(9,82 m·s^-2) = 53,13 m·kg·s^-2 = 53,13 N.

   Dvs. opdriften på ankeret er 53,1 N

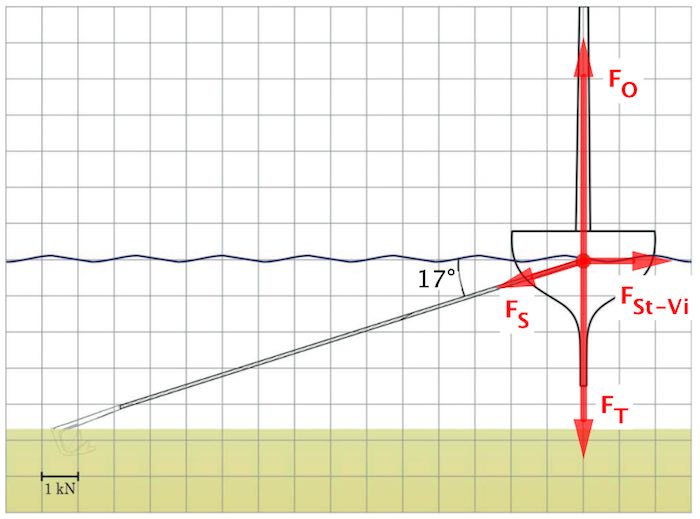
3. Da båden ikke bevæger sig vil den resulterende kraft på den være nul i følge Newtons første lov. Den resulterende kraft er summen af følgende kræfter:

   Tyngdekraften (F_T) virker nedad i bådens massemidtpunkt (det røde punkt). Dens størrelse er lig med bådens masse gange tyngdeaccelerationen, dvs. |F_T| = (560 kg)·(9,82 m·s^-2) = 5,50 kN.

   Opdriften (F_O) virker opad i bådens opdriftpunkt, der her tænkes at være det røde punkt. Størrelsen er 6,22 kN.

   Kraften fra Strøm og vind (F_St-Vi) påvirker båden med en vandret kraft, der vil virke i det røde punkt.

   Snorkraften (F_S) fra ankeret påvirker båden skråt nedad fra fortøjringspunktet på båden (her: det røde punkt) ned mod forankringspunktet på bunden.

   Snorkraftens vandrette komposant (F_S,v) har samme størrelse som strøm- og vindkraften.

   Dens lodrette komposant (F_S,l) har samme størrelse som forskellen mellem tyngdekraft og opdrift (F_O - F_T), idet ankertovet vil trække båden nedad, så mere af den er under vandet. (Uden forankring er F_O - F_T = 0.)

   Der gælder, at |F_S,v| = |F_S|·cos(17°) og |F_S,l| = |F_S|·sin(17°).

   Forskellen mellem opdrift og tyngdekraft er |F_O - F_T| = (6,22 - 5,50) kN = 0,754 kN.

   Heraf findes |F_S|, idet man har: |F_S|·sin(17°) = 0,754 kN ⇒ |F_S| = (0,754 kN)/sin(17°) = 2,58 kN.

   Til sidst findes størrelsen af kraften fra strøm og vind: |F_St-Vi| = |F_S|·cos(17°) = (2,58 kN)·cos(17°) = 2,47 kN.

   Kræfterne tegnes ind i diagrammet: