Svar på opgave 1: Gravity Probe-B

1. P = ΔE/Δt, hvor

      P er effekt,

      ΔE er den tilførte energi og

      Δt er den forbrugte tid.

   Man får: Δt = ΔE/P = (5,40·10³ J)/(12,8 J/s) = 422 s. (7,03 min.)

   Dvs. det tager 422 sek. at opvarme heliummet.

2. P = ΔE/Δt = m·c_p·ΔT/Δt ⇒

   m = P·Δt/(c_p·ΔT) = (12,8 W)·(422 s)/[(2,1·10³ J/(kg·K))·(1,838 K - 1,826 K)] = 2,1·10² kg

   Her gælder, at:

      m er massen af helium,

      c_p er heliums specifikke varmekapacitet og

      ΔT er heliummets opvarmning i Kelvin.

   Der er 2,1·10⁵ g He, og der bruges 30 g pr. time.

   Dvs. He-beholdningen rækker: (2,1·10⁵ g)/(30 g/time) = 7000 timer = 2,9·10² døgn

Svar på opgave 2: Radioaktivt sporstof

1. Elektronindfangning foregår ved, at kernen i et moder-grundstof (Y) optager en af elektronerne fra sin inderste skal og derved omdannes til et datter-grundstof (X) med et atomnummer (Z), der er een mindre end moder-grundstoffet. Massetallet (A) bevares. Den manglende elektron bliver erstattet af een udefra. Der afgives en neutrino (ν_e). Det generelle reaktionsskema er:

   

   Her er X lig med Rb-isotopen med massetallet 82. Dette giver følgende reaktionsskema:

   

2. Antallet af henfald kan beregnes som integralet af aktiviteten fra t = 0 til t = 4,0 min. Man har:

   A(t) = A₀·e^-k·t, hvor

      A(t) er aktiviteten af henfald for Rb-82,

      A₀ er start-aktiviteten = 1,48 GBq,

      k er henfaldskonstanten = ln(2)/T_1/2 = ln(2)/(1,26 min) = 0,550 min^-1 og

      t er tiden i minutter.

   T_1/2 er halveringskonstanten for henfald af Rb-82. (Det, man så på i a, var dannelsen af Rb-82.)

   

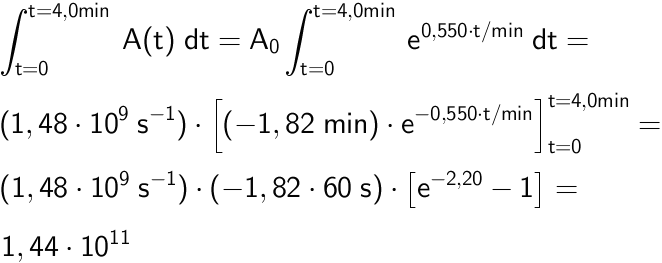
   Dvs. der sker 1,44·10¹¹ henfald af Rb-82 på 4,0 minutter.

Svar på opgave 3: Proxima Centauri

1. Man bruger Wiens forskydningslov.

   λ_max = (2,898·10^-3 m·K)/T, her er

      λ_max er den bølgelængde, der giver den højeste intensitet og

      T er stjernens effektve overfladetemperatur = 2,67·10³ K.

   Man får: λ_max = (2,898·10^-3 m·K)/(2,67·10³ K) = 1,09·10^-6 m.

   Dvs. den bølgelængde, hvor intensitetsfordelingen har sit maksimum, er 1,09·10^-6 m

2. Man finder stjernens radius ved hjælp af Stefan-Boltzmanns lov.

   L = 4·π·r²·σ·T⁴, hvor

      L er luminositeten = stjernens samlede effekt = 4,41·10²² W,

      r er stjernens radius,

      σ er Stefan-Boltzmanns konstant = 5,67·10^-8 W·m^-2·K^-4 og

      T er stjernens effektive overfladetemperatur = 2,67·10³ K.

   Man får heraf:

   r = √[L/(4·π·σ·T⁴)] = √[(4,41·10²² W)/(4·π·(5,67·10^-8 W·m^-2·K^-4)·T⁴)] = 3,49·10⁷ m.

   Dvs. stjernens radius er 3,49·10⁷ m

3. Der gælder i et cirkulært omløb med konstant omløbsfart, at tyngdekraften er lig med centripetalkraften. Dobbeltstjernens masse tænkes samlet i dens massemidtpunkt.

   Tyngdekraft = G·(M·m/r²) og centripetalkraft = m·v²/r.

      G er gravitationskonstanten = 6,674·10^-11 N·m²·kg^-2 = 6,674·10^-11 m³·s^-2·kg^-1

      M er dobbeltstjernens mase = 4,01·10³⁰ kg,

      m er stjernens masse (går ud i beregningen),

      r er omløbsbanens radius = 0,18 ly = 0,18·9,46·10¹⁵ m = 1,703·10¹⁵ m og

      v er stjernens fart i omløbsbanen (går ud i beregningen).

   G·(M·m/r²) = m·v²/r ⇒ G·(M/r) = v²

   Der gælder følgende sammenhæng mellem farten og omløbstiden (T) i en jævn cirkelbevægelse:

   v = 2·π·r/T.

   Tilsammen fås følgende ligning for T:

   G·M/r = v² ⇒ G·M/r = (2·π·r/T)² ⇒ T = √[4·π²·r³/(G·M)] =

   √[4·π²·(1,703·10¹⁵ m)³/((6,674·10^-11 m³·s^-2·kg^-1)·(4,01·10³⁰ kg))] = 2,70·10¹³ s

   Dvs. omløbstiden for stjernen er 2,70·10¹³ s = 8,55·10⁵ år

   Alternativt:
   Der gælder følgende for en planet i cirkulært omløb omkring solen: T = √[4·π²·r³/(G·M)].
   Formlen er udledt fra Keplers 3. lov, der bygger på ellipseformede baner.
   Herfra generaliserer man fra solsystemet til det konkrete tilfælde.

Svar på opgave 4: Kanonkonge

1. Det antages, at kanonkongen accelererer med konstant lineær acceleration, som er lig med gennemsnits-accelerationen.

   Der gælder følgende formler for distancen som funktions af tiden, s(t), og farten som funktion af tiden, v(t), når han har accelerationen, a, i kanonen:

   s(t) = 0,5·a·t² og v(t) = a·t.

   Det antages, at han forlader kanonen til tiden t₁, hvorved der gælder, at:

   s(t₁) = 5,1 m og v(t₁) = 60 km/h = 60·(1000m)/(3600 s) = 16,67 m·s^-1.

   Dette giver to ligninger med de to ubekendte a og t₁, som løses i Ti-Nspire:

   solve(5.1=0.5*a*t₁² and 16.67=a*t₁ and t₁>0,a,t₁) ▸ a=27.2 and t₁=0.612

   Dvs. kanonkongens gennemsnits-acceleration er 27 m·s^-2

2. Man bruger formlen for sammenhængen mellem højde, h(x), og længde, x, i et skråt kast:

   h(x) = (-0,5·g·x²)/[(v₀)²·(cos(α))²] + tan(α)·x, hvor

      g er tyngdeaccelerationen = 9,82 m·s^-2,

      v₀ er farten for kanonkongen i kanonløbets retning, idet han forlader kanonen =
      60 km/h = 16,67 m·s^-1 og

      α er den vinkel i forhold til vandret, som han skydes afsted i = 35°.

   Man får: h(x) = −0,0263·x² + 0,700·x.

   Man løser ligningen h(x) = -3,2 for x > 0 i Ti-Nspire og får:

   solve(−3.2=−0.0263*x²+0.7*x and x>0,x) ▸ x=30.6

   Opgaven han også løses grafisk. Nedenstående løsning er lavet i Geogebra:

   

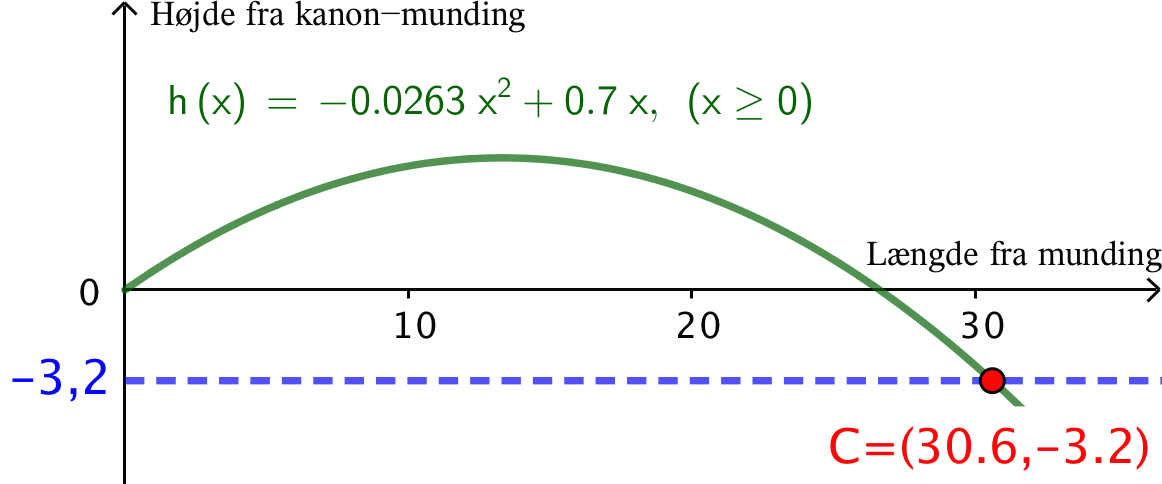
   Dvs. kanonkongen flyver en distance af 31 m før han lander.

Svar på opgave 5: Automatisk parkeringskælder

1. Tyngdekraften på elevator med last kaldes F_T. Der gælder at:

   F_T = m·g = (2,5·10³ kg)·(9,82 m·s^-2) = 24,6 kN

2. Den distance, som elevatoren bevæger sig nedad, er lig med den numeriske værdi af arealet under kurven for farten som funktion af tiden.

   På figuren nedenunder er markeret de tidspunkter, hvor farten ændres, for nemmere at kunne beregne arealet:

   

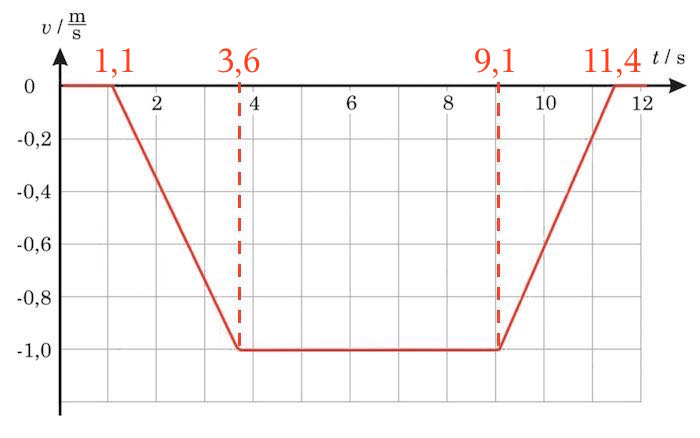
   Forklaring til kurven:
   0<t<1,1s: Elevatoren holder stille (kurven ligger på x-aksen).
   1,1s<t<3,6s: Elevatoren bevæger sig nedad med konstant fartforøgelse (kurven er en ret linje, der fjerner sig fra x-aksen for voksende t).
   3,6s<t<9,1s: Elevatoren bevæger sig nedad med konstant fart (kurven er en ret linje under x-aksen og parallel med denne).
   9,1s<t<11,4s: Elevatoren bevæger sig nedad med konstant fartformindskelse (kurven er en ret linje under x-aksen, der nærmer sig x-aksen for voksende t).
   11,4<t: Elevatoren holder stille igen.

   Arealet er:

   0,5·(3,6 s - 1,1 s)·(1,0 m·s^-1) + (9,1 s - 3,6 s)·(1,0 m·s^-1) + 0,5·(11,4 s - 9,1 s)·(1,0 m·s^-1) =

   0,5·2,5 m + 5,5 m + 0,5·2,3 m = 7,9 m.

   Dvs. elevatoren flytter sig 8 m nedad.

3. Den resulterende kraft (F_R) på elevatoren er givet ved: F_R = m·a, hvor m er elevatorens masse inklusive last, og a er dens acceleration.

   Ved t = 10 s bremser elevatoren på vej nedad, dvs. den resulterende kraft peger opad, modsat tyngdekraften. Opbremsningen skabes af de to snorekræfter fra kablerne. Kraftdiagrammet for elevatoren for t = 10 s er vist nedenfor:

   

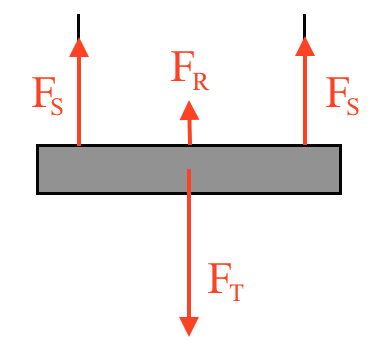
   Ved t = 10 s er a = (1,0 m·s^-1)/(2,3 s) = 0,44 m·s^-2.

   Man har: F_R = 2·F_S + F_T (den resulterende kraft er summen af de kræfter, der virker på elevatoren). Dette gælder for kræfterne som vektorer. Man skal nu finde størrelsen af snor­kræfterne.

   Man ser af kraftdiagrammet, at alle kræfter er parallelle. Dermed kan vektorerne omskrives til hver vektors størrelse med et fortegn. Idet positiv retning regnes opad får man:

   |F_R| = 2·|F_S| - |F_T| ⇒ |F_S| = (|F_R| + |F_T|)/2 = m·(a + g)/2 =

   (2,5·10³ kg)·(0,44 m·s^-2 + 9,82 m·s^-2)/2 = 1,28·10⁴ N.

   Dvs. kraften i hvert kabel er 13 kN

Svar på opgave 6: Nære galakser

1. Der gælder følgende sammenhængen mellem galaksens fart, v, rødforskydningen, z, og lysets fart, c (= 3,00·10⁸ m·s^-1):

   v = z·c

   Dvs. galaksens fart er 0,03005·3,00·10⁸ m·s^-1 = 9,02·10⁶ m·s^-1

2. Hubbles lov er: v = H₀·D, hvor

      v som før er galaksens fart i forhold til jorden (m·s^-1),

      H₀ er Hubbles konstant og

      D er galaksens afstand i forhold til jorden (angivet i m, idet 1Mly = 9,46·10²¹ m).

   Man opretter lister i Ti-Nspire med afstande (afstand) i m og bølgelængder (bølgelængde) i nm:

   afstand:={304,367,399,439,495,658,817,890}*9.46*10²¹ ▸ {2.876E24,3.472E24,3.775E24,4.153E24,4.683E24,6.225E24,7.729E24,8.419E24}

   bølgelængde:={671.2,673.6,674.9,676.,679.2,685.7,693.3,697.5} ▸ {671.2,673.6,674.9,676.,679.2,685.7,693.3,697.5}

   Dernæst oprettes en liste med z-værdier for hver bølgelængde:

   z:=(bølgelængde-656.28)/656.28 ▸ {0.02273,0.02639,0.02837,0.03005,0.03492,0.04483,0.05641,0.06281}

   Endelig oprettes en liste med v, som er lig med z·c:

   v:=z*3.*10⁸ ▸ {6.820E6,7.917E6,8.512E6,9.014E6,1.0477E7,1.345E7,1.692E7,1.884E7}

   Man laver et plot af v som funktion af D:

   

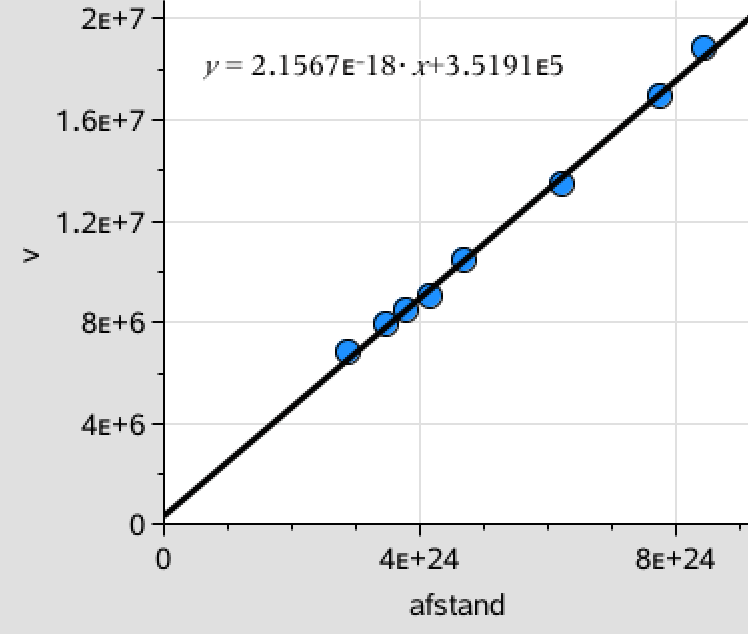
   Plottets lineære tendenskurve er v = (2,16·10^-18 s^-1)·D + (3,52·10⁵ m·s^-1).

   (Plottet burde gå igennem (0,0), men afvigelsen ser ud til at kunne forklares med måleusikkerhed.)

   Da Hubbles konstant er hældningen til kurven, så får man, at den er lig med 2,2·10^-18 s^-1

Svar på opgave 7: Armstrækninger

1. Personen antages at være 1,75 m og veje 65 kg (= m). Personen massemidtpunkt tænkes at blive løftet 0,3 m (= Δh) for hvert stræk. Hvert stræk antages at tage 0,5 s (= Δt).

   Effekten (P) er lig med gennemsnitlig ændring i potentiel energi pr. tidsenhed, dvs:

   P = m·g·Δh/Δt = (65 kg)·(9,82 m·s^-2)·(0,3 m)/(0,5 s) = 383 W.

   Dvs. effekten i hver armstrækning er 3,8·10² W